Nous commençons une suite de cours représentant la
trace écrite que les élèves doivent relever et savoir.
Ceci ne saurait remplacer un livre de Physique Chimie. Quelques exercices
originaux seront proposés, avec leur corrigé.
On ne connaît pas sa taille.
Les télescopes permettent de voir jusqu'à 10 26
m.
Il comporte des milliards de galaxies.
Elles comportent des milliards d'étoiles.
Notre galaxie est la Voie lactée. Elle comprend 200 milliards
d'étoiles et s'étend sur 10 21 m.
La plus proche galaxie est Andromède, à 2 x 10 22
m.
Notre étoile est le Soleil ; il est à 150 millions
de kilomètres, soit 1,5 x 10 11 m.
L'étoile la plus proche du Soleil est Proxima du Centaure, à
4 x 10 16 m.
Les bactéries, observables au microscope optique, mesurent
quelques micromètres.
Sa taille est de l'ordre de 10 -10 m. On peut le détecter
et le manipuler grâce au microscope à effet tunnel. Sa structure
est lacunaire.
En notation scientifique, un nombre n s'écrit :
n = a . 10 p
où a est un nombre décimal comportant un seul chiffre, différent de 0, devant la virgule, ce qui peut se noter :
1 inférieur ou égal à a, lui-même strictement inférieur à 10.
Une erreur est fréquemment commise, en entrant un nombre
en notation scientifique dans une calculatrice :
Si vous souhaitez entrer le nombre 7,3 . 10 3, faites 7,3 puis EE ou Exp (selon les calculatrices) puis 3. Le nombre 10 est toujours sous-entendu. Essayez. En cas de doute, par exemple un jour de contrôle, entrez 1 . 10 2 dont vous savez qu'il vaut 100 et vérifiez ce qu'affiche votre calculatrice.
| Facteur multiplicatif | Préfixe | Symbole |
| 10 -15 | femto | f |
| 10 -12 | pico | p |
| 10 -9 | nano | n |
| 10 -6 | micro | |
| 10 -3 | milli | m |
| 10 3 | kilo | k |
| 10 6 | méga | M |
| 10 9 | giga | G |
| 10 12 | téra | T |
Dans la notation scientifique n = a . 10 p, les chiffres
utilisés pour écrire le décimal a sont appelés
chiffres significatifs. Le nombre de chiffres significatifs indique la
précision de la mesure.
En physique, 4 . 10 7 m et 4, 0 . 10 7 m n'ont pas la même signification.
Pages 179 et suivantes, exercices n° 12, 13, 23, 25, 35.
Vous devez mesurer la distance à laquelle se trouve une cible
inaccessible directement pour diverses raisons. Vous disposez d'une (ou
deux) planche(s) à dessin et d'épingles.
Votre résultat sera inscrit au tableau, puis comparé
à la "bonne" valeur.
Réflexion : Donnez quelques cas, où il peut être utile de mesurer une distance entre deux points, sans se déplacer de l'un à l'autre.
Il s'agit d'un travail pratique très subtil et formateur.
Car selon la finesse de la manipulation, l'erreur sur le résultat
de la mesure peut aller de 30 % à moins de 1 %.
Les résultats des élèves pourront faire l'objet
d'un traitement statistique (écart type, estimateur de la "bonne"
valeur, c'est à dire moyenne des mesures ne semblant pas aberrantes).
Il parait donc judicieux que la mesure directe la plus précise
possible, de la distance recherchée par les élèves,
ait été faite au préalable, et que ce résultat
soit inscrit au tableau par le professeur, mais caché ; puis que
les différents groupes d'élèves viennent inscrire
leurs résultats ; puis qu'après estimation du "bon" résultat
des élèves, la "vraie" valeur soit dévoilée.

Trouver une démarche permettant d'obtenir un bon résultat est la partie la plus formatrice de ce travail pratique ; il semble donc qu'il faille éviter ici de donner aux élèves un protocole expérimental à suivre.
Le raisonnement de la classe guidée par le professeur doit conduire
aux idées suivantes :
Cela amène aux décisions suivantes :
Remarques importantes :
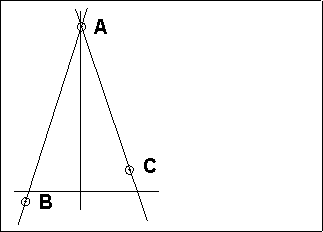
Il n'est absolument pas nécessaire que BC soit parallèle à la base de la planche ; il suffit de tracer un trait parallèle à cette base puis sa perpendiculaire.
Voici une autre erreur souvent observée :
Pour mesurer l'abscisse des points A, B et C, beaucoup d'élèves
les projettent sur l'axe des abscisses. La figure qui suit montre bien
que la moindre imperfection de tracé conduit à une erreur
désastreuse.
Par contre, observons comment l'ordonnée du point D peut se
mesurer, sans tracé et avec précision : DD' et DD" ont des
longueurs très proches, malgré une erreur flagrante de positionnement
de la règle DD".
Pour une bonne précision, la règle servant à mesurer la base de triangulation et la "vraie" distance doit être la même (prendre un décamètre à ruban). Les mesures sur la planche à dessin doivent se réaliser avec le même instrument (ce qui se fait naturellement) ; par contre le calcul montre que si la règle élève et le décamètre ont des graduations différentes, mais régulières, cela ne causera pas d'écart entre mesure directe et mesure par triangulation. Mais si le décamètre est faux, ce sont ces deux résultats qui seront faussés de la même façon?
En fait un double décamètre bas de gamme (ruban en fibre de verre), comparé à un mètre ruban de haute qualité, s'est révélé étonnamment bon.
Salle 14 :
Mesure directe, avec double décamètre fibre de verre,
sur la terrasse :
Distance mur (14) - joint de mur en face : 31,22 m
Epaisseur du mur (14) jusqu'à la fenêtre : 0,251 m
Epaisseur de la fenêtre jusqu'à l'intérieur de
la vitre : 0,022 m
Total : 31,493 m.
Mesure par triangulation :
Base du triangle : 7,8 cm
Hauteur du triangle : 28,6 cm
Translation de la planche : 8,75 cm.
Distance calculée : 28,6 / 7,8 x(8,75 + 0,078) = 32,37 m
Distance mesurée directement : 31,493 + 0,286 = 31,78 m.
Les marins savent depuis l'antiquité grecque, que de l'huile
lâchée à la surface de la mer, s'étale sur une
très grande surface.
Benjamin Franklin (1706 - 1790) fait l'expérience sur un étang.
Une goutte d'huile d'olive s'étale sur prés de 100 m2.
Versez de l'eau dans le cristallisoir bien propre, attendez que
le liquide soit au repos, et saupoudrez un tout petit peu de talc sur toute
la surface de l'eau, ou mieux de fleur de soufre.
Laissez tomber, au milieu du cristallisoir, une goutte d'huile d'olive
diluée 1000 fois (en volume) dans un solvant volatil (acétone,
essence de térébenthine ... ).
Observez attentivement ce qui se passe alors.
Mesurez le diamètre de la tache d'huile.
A l'aide d'une pipette, mesurez le volume d'une goutte d'huile, par
exemple, en comptant le nombre de gouttes contenu dans 1 mL.
Calculez l'aire (surface) de la tache d'huile.
Calculez le volume d'une goutte d'huile.
Calculez l'épaisseur de la tache d'huile, égale à
la longueur d'une molécule.
Lancez le logiciel ChemSketch. S'il s'agit d'une version non enregistrée,
regardez défiler la liste des logiciels proposés par ACD
Labs, et de leurs possibilités.
Quand cela devient possible, cliquez sur Annuler.
Ouvrez le fichier MolChemsk ; il comporte une représentation en deux dimensions de la molécule d'acide oléique (c'est la plus grande).
Il vous reste à la visualiser en trois dimensions. Dans les menus déroulants, faites ACD/Labs | 3D Viewer.
La fenêtre 3D apparaît, vide. Repassez à ChemSketch, par un bouton en bas de votre écran, cliquez sur l'outil Lasso, et sélectionnez la molécule, en cliquant dessous. En bas de l'écran, cliquez sur Copy To 3D.
Différentes visualisations sont possibles, ainsi que des animations très belles.
Si votre molécule apparaît toute plate, faites 3D Optimization (icône en forme de molécule de méthane).
Vous pouvez ensuite mesurer la distance entre les centres de différents atomes.
Déduisez en la longueur de la molécule.
1.Pourquoi les marins jetaient ils de l'huile à la mer ?
2.Que savez vous de Benjamin Franklin ?
3.Pourquoi l'huile a t elle été diluée 1000 fois
?
4.Comment prouver que le solvant s'est bien évaporé ?
5.Il y a dans cet énoncé des hypothèses cachées,
lesquelles ?
L'expérience est plus spectaculaire en employant l'essence
de térébenthine comme solvant : On voit nettement des irisations
interférentielles qui disparaissent au bout de quelques dizaines
de secondes, preuve que la première épaisseur de la tache
est de l'ordre du micron, puis que l'essence s'évapore. Par contre,
les résultats numériques ne sont pas très bons, la
tache fait 20 ou 14 cm de diamètre ; elle est donc trop mince (reste-t-il
de la térébenthine, ou celle-ci modifie-t-elle la position
des molécules d'huile ? ).
L'acétone conduit à une tache d'environ 13 cm de diamètre
qui se réduit rapidement à 9 ou 10 cm. Attention à
ne pas trop approcher la pipette de la surface de l'eau, car les vapeurs
d'acétone chassent le talc.
52 gouttes correspondent à 1 mL. Avec l'acétone, la
tache fait environ 9,5 cm de diamètre, soit une épaisseur
de 2,7 nm. ChemSketch, après optimisation 3D donne une longueur
de 2,3 nm, pour la molécule d'acide oléique.
1.Jeter de l'huile à la mer permet de diminuer la violence
des vagues.
2.B. Franklin nait en 1706 à Boston. Il est l'inventeur du paratonnerre.
En 1776, il préside la Convention Constitutionnelle de Philadelphie
; il est l'un des auteurs de la Déclaration d'Indépendance.
En 1778, il arrive en France, en tant qu'ambassadeur de la République
du Nouveau Monde. Il rentre aux États-Unis en 1785.
3.La dilution est nécessaire si votre cristallisoir ne couvre
pas 100 m2.
4.Vous pouvez recommencer l'expérience dans un cristallisoir
propre, en employant uniquement le solvant : Le talc s'écarte, puis
le trou se referme. Si vous êtes très observateur, vous avez
du voir des irisations de couleur, lorsque la goutte est tombée
sur l'eau, irisations qui ont ensuite disparu. Ces irisations correspondent
à une épaisseur de l'ordre de la longueur d'onde de la lumière
visible, soit en gros 1 micron, ou 10-6 m. Leur disparition correspond
à l'évaporation du solvant.
5.Il est supposé que l'huile d'olive est constituée de
molécules ayant toutes la même taille, et que ces molécules
se "dressent" à la surface de l'eau.
Dans un milieu transparent et homogène, la lumière
se propage en ligne droite.
Par exemple, dans le vide, loin d'une masse importante ; dans l'air si la température est en tous points la même.
Voir le travail pratique sur la mesure du diamètre d'un cheveu,
chapitre TP MPI.
En 1674, l'astronome Danois Ròmer, travaillant à l'observatoire
de Paris, effectue la première mesure, à partir de l'observation
(sur Terre) du mouvement des satellites de Jupiter.
La vitesse de la lumière dans le vide est une constante universelle.
Par définition, elle vaut :
c = 299 792 458 m . s -1.
En fait, ceci est la définition actuelle du mètre.
| c vaut environ 3 . 10 8 m . s -1, soit 300 000 km . s -1. |
Aucun objet possédant une masse ne peut atteindre cette vitesse. Dans les autres milieux transparents, la lumière va moins vite. 200000 km / s dans le verre.
Pages 194 et suivantes, exercices n° 12, 23, 24, 26, 27, 28.
(Les deux derniers pour les élèves les plus rapides).
Vous ne devez jamais pointer le laser vers les yeux d'un camarade
(ni vers les vôtres).
En effet, la puissance du laser est faible, mais votre cristallin la
concentrerait sur une petite surface de rétine qui s'en trouverait
irrémédiablement détruite.
Vous allez mesurer le diamètre d'un cheveu, à l'aide
d'un laser.
Lorsque de la lumière rencontre un obstacle qui l'arrête
partiellement, elle ne se propage pas en ligne droite : C'est le phénomène
de diffraction. Ce phénomène est particulièrement
visible avec la lumière d'un laser.
Place dans le faisceau du laser différents obstacles de diamètres
d connus.
Mesure la largeur L d'une tache latérale de diffraction.
Représente graphiquement la fonction L = f (d).
Mesure la largeur d'une tache latérale de diffraction donnée
par un cheveu.
Trouve sur le graphique le diamètre du cheveu, par interpolation.
1.Quelle est la méthode la plus précise pour évaluer
la largeur de la tache latérale ?
2.A puissance égale quel est le laser le plus dangereux : le
laser infra rouge, ou le laser rouge ?
1.Il faut repérer de chaque côté d'une tache
latérale, le milieu de la zone obscure. Il est encore plus précis
de mesurer ainsi la taille de plusieurs taches.
2.Le laser infra rouge est plus dangereux, car sa lumière est
invisible. Ce n'est que lorsque sa rétine sera très brûlée,
que la victime s'en apercevra.
La tache centrale n'est pas utilisable ici, car les fils étant
transparents, elle est à la fois figure de diffraction et d'interférences.
Vous pourrez aussi consulter sur ce site, le chapitre TP, MPI, où
plusieurs expériences de cours sont présentées.
Sommaire : Décomposition de la lumière blanche, longueur d'onde, la réfraction, la dispersion, couleurs primaires, couleurs complémentaires, travail pratique : réfraction de la lumière.
Schéma simpliste de l'expérience :
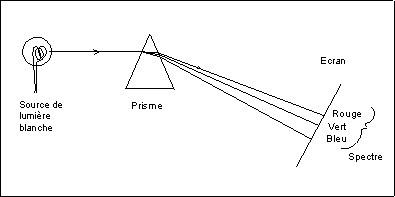
Un prisme permet de décomposer la lumière blanche.
La lumière blanche est polychromatique,
la lumière du laser est monochromatique.
Chaque radiation colorée est caractérisée par une longueur d'onde (mesurée dans le vide). Le laser du laboratoire de physique a une longueur d'onde de 632,8 nm. L'oeil humain n'est sensible qu'aux radiations comprises entre 400 et 800 nm.
|
|
|
|
|
|
| 800 nm |
400 nm
|
// La lumière est une vibration électromagnétique.
Lorsque la lumière traverse la surface séparant deux
milieux transparents différents, elle subit un changement de direction
: C'est la réfraction.
Celle-ci sera étudiée en travail pratique.
L'indice d'un milieu matériel transparent dépend de
la longueur d'onde de la lumière. Ce milieu est dispersif.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pages 208 et suivantes, exercices n° 15, 17, 18, 19, 23.
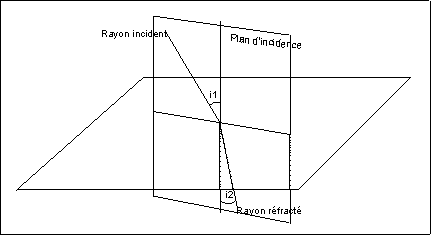
Première loi de la réfraction (Snell Descartes)
:
| Le rayon réfracté est dans le plan d'incidence. |
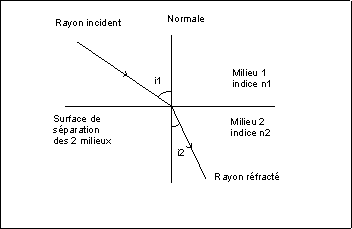
Deuxième loi de la réfraction :
| n1 . sin i1 = n2 . sin i2 |
où n1 est l'indice de réfraction du milieu 1 et n2 celui du milieu 2.
L'indice de l'air est égal à 1.
| Note : v = c / n |
avec v vitesse de la lumière dans le milieu d'indice n et c vitesse de la lumière dans le vide.
Voir aussi le chapitre TP, MPI de ce site.
Sommaire : Les spectres d'émission, continus, de raies ; les spectres d'absorption, de raies, de bandes ; application à l'astrophysique ; expériences, travaux pratiques.
Un corps chaud (solide, liquide, ou gaz sous haute pression) émet
une lumière dont le spectre est continu. Lorsque la température
du corps s'élève, le spectre devient plus lumineux et plus
riche en couleurs bleue et violette.
Un gaz à basse pression, traversé par de la lumière
blanche, absorbe les radiations qu'il est capable d'émettre lorsqu'il
est chaud. Le spectre obtenu comporte des raies noires d'absorption.
La chlorophylle, en solution, donne un spectre d'absorption de bandes,
caractéristique des molécules. Le permanganate de potassium
dans l'eau donne une solution 'violette', en fait de couleur magenta. Cette
solution absorbe donc la couleur complémentaire du magenta, c'est
à dire le vert. Le spectre d'absorption laisse apparaître
plusieurs bandes d'absorption dans le vert.
L'étude du spectre d'une étoile permet de trouver
:
Pages 222 et suivantes, exercices n° 13, 14, 15 (voir page 199
la table de correspondance entre couleur et longueur d'onde), 21.
Vous pouvez consulter le chapitre TP, MPI, pour des démonstrations
de cours. Voici quelques idées supplémentaires :
Couleurs complémentaires, avec des filtres colorés et un rétroprojecteur.
Les élèves peuvent observer chez eux le spectre de raie d'émission du sodium. Il leur faut un réseau et une fente source formée par... un tortillon de papier hygiénique auquel on met le feu. Attention aux risques d'incendie !
Observation depuis leur place, à l'aide de spectroscopes de poche, des spectres émis par des lampes spectrales, Na, Hg, Ne.
Comparaison des spectres émis par une lampe à vapeur de sodium et par un bec Bunsen, réglé pour que sa flamme soit éclairante.
Spectres d'absorption, en observant l'ombre portée d'une baguette de verre chauffée dans la flamme d'un bec Bunsen, éclairée par une lampe à vapeur de sodium et une lampe à vapeur de mercure.