| EXEMPLES D’ACTIVITÉS | CONTENUS | CONNAISSANCES
ET SAVOIR-FAIRE EXIGIBLES |
| Textes (Galilée, Newton, Einstein, Feynman, etc.).*
Applications de la vie courante mettant en jeu la première et
la troisième loi de Newton.
|
1. La mécanique de Newton
Lien qualitatif entre S F ext et DvG (rappels) Comparaison de DvG correspondant à des intervalles de temps égaux pour des forces de valeurs différentes (résultat de l’activité) Introduction de DvG /Dt Accélération : aG = lim Dt ->0 (DvG /Dt) = dvG /dt ; vecteur accélération (direction, sens, valeur). Rôle de la masse. Deuxième loi de Newton appliquée au centre d’inertie. Importance du choix du référentiel dans l’étude du mouvement du centre d’inertie d’un solide : référentiels galiléens. Troisième loi de Newton : loi des actions réciproques (rappel). |
Choisir un système. Choisir les repères
d’espace et de temps. Faire l’inventaire des forces extérieures appliquées à ce système. Définir le vecteur accélération et exploiter
cette définition, connaître son unité.
|
// Note : Le nombre de séances de
travaux pratiques accordées à chaque séquence est
indicatif et provient du programme officiel.
Sommaire : Introduction, étude des lois
de conjugaison, lentille convergente, travail pratique : Objet réel,
image réelle ; objet virtuel, image réelle ; objet réel,
image virtuelle ; loi de conjugaison en position.
Commençons par quelques généralités,
permettant de mieux comprendre comment le nouveau programme d'optique de
première S peut enrichir celui de spécialité
physique de terminale S, et réciproquement.
Qu'apporte de nouveau la façon de traiter le programme d'optique, telle que préconisée dans les documents d'accompagnement de première S ? Une approche expérimentale différente (et complémentaire de l'approche plus traditionnelle).
Les méthodes proposées plus loin sont plus performantes
que celles habituelles, chaque fois qu'il faut étudier une image
virtuelle,
donnée par une lentille divergente ou une loupe ou un oculaire,
car il est inutile d'employer une modélisation d'œil accommodant
à une distance finie ou infinie. Par contre, elles sont moins rapides
que l'utilisation d'un écran pour l'étude des images réelles.
Mais rappelons qu'un écran permet de situer la position d'une image, trouver sa taille, mais que diffusant les rayons de lumière qui forment cette image, il ne permet pas en réalité son observation. L'écran permet par contre de comprendre le phénomène de formation d'une image sur la pellicule d'un appareil photographique.
Pensez à l'étude selon la méthode classique, de l'image virtuelle donnée par une loupe (ou une lentille divergente), reprise par un modèle d'œil accommodant à distance finie (qu'il faut mesurer), qui donne sur son écran rétine, une image inversée (quand on regarde du bon côté de la rétine) donc droite puisque le cerveau lui-même retourne l'image. Ouf ! Alors qu'il suffit de regarder dans la loupe pour voir ce qui se passe ! Et que des méthodes de mesure rapides et suffisamment précises sont proposées au paragraphe suivant.
qui peuvent être montrés sur tableau magnétique
et testés par les élèves sur leur banc d’optique.
// Le professeur insistera sur le fait que la lanterne du tableau magnétique ne donne pas des rayons de lumière, mais des pinceaux à section rectangulaire, qui ‘plongent’ vers le tableau magnétique et le rencontrent en une série de points alignés qui simulent le tracé du parcours d’un rayon de lumière.

Sens de propagation de la lumière ---->
Si on place un écran avant (en se référant au sens de propagation de la lumière) A’, on obtient une tache : ce n’est PAS une image. En A’, la tache est « ponctuelle » ; c’est l’image de A. Après A’ la tache s’agrandit, ce n’est PAS une image. A proprement parler, la présence de l’écran modifie le trajet de la lumière et l’image n’est pas celle que voit l’œil, mais celle qui se formerait sur la surface sensible dans un appareil photographique.
L’image virtuelle B’ peut être observée à l’œil nu.
Avec le banc d’optique, une lettre lumineuse et un écran, étudiez la loi de conjugaison en position, avec une lentille convergente de vergence 8 dioptries.
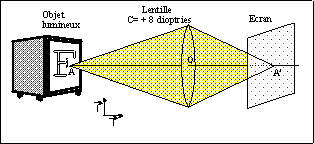
Pour un objet placé 40 cm avant la lentille (vous vous référez au sens de propagation de la lumière), cherchez plusieurs fois de suite la position de l’image. Quelle est votre conclusion ?
Réponse : Nous observons une latitude de mise au point. Nous prendrons le résultat moyen.
Pour une image placée 20 cm après la lentille, cherchez les positions extrêmes de l’objet A telles que son image soit nette. Conclusion ?
Réponse : Nous observons une profondeur de champ.
Remplissez le tableau de mesures suivant :
| p (en m) | -1,25 | -0,65 | -0,35 | -0,25 | +0,10 | -0,075 |
| p’ (en m) | ||||||
| Voir paragraphe 2 3 | Voir paragraphe 2 4 |
Dans ce cas, l’objet est virtuel, donc situé après
la lentille, à 10 cm, dans le sens de la lumière. Il est
créé par une lentille L2 de 5 dioptries (obtenue en accolant
2 lentilles de +2 dioptries et de +3 dioptries).

A’1 image réelle de A1 pour la lentille L2 devient A2 objet virtuel pour la lentille étudiée L1, qui en donne une image réelle A'2.
Dans ce cas, l’objet réel est près de la lentille
convergente, avant celle-ci, à une distance inférieure (en
valeur absolue) à la distance focale. Son image est virtuelle. Elle
ne peut pas être obtenue sur un écran sans système
complémentaire. Elle peut être observée à l’œil
nu ou à l’aide d’un modèle d’œil.
La première méthode est la plus simple si vous suivez le protocole suivant :
Observez la lettre lumineuse, directement à travers la lentille, en prenant garde à ne pas être ébloui. Vous observez une image droite, agrandie.
Éteignez la lanterne et éclairez la lettre à l'aide d'une lampe de bureau ; vous pouvez affiner vos observations. Mais la lanterne gêne les mesures. Retirez du banc d'optique la lentille de 8 dioptries avec son support. Posez celui-ci sur votre table, en couchant le support ; replacez l'objet à une distance de 8,0 cm avant la lentille. Variante : Laissez la lentille sur le banc d'optique, enlevez la lanterne et pincez la lettre dans le support d'écran.
Il est possible de trouver la position de l'image et sa taille approximatives (avec une précision correcte) à l'aide d'un réticule constitué par une équerre ou une règle graduées.
Choisissez éventuellement un objet plus pratique que la lettre, un petit carton portant près de son bord gauche un ou plusieurs rectangles de 15 x 15 mm (ou 10 x 10 mm). Observez-le à travers la lentille. Placez la règle de manière à ce qu'en bougeant la tête, sa partie visible directement au-dessus de la lentille paraisse fixe par rapport à l'image du carton vu à travers la lentille. Constatez que la règle doit être plus éloignée de la lentille que le carton ; repérez sa position. Déplacez légèrement la règle vers la gauche, de manière que ses graduations soient visibles directement et mesurez ainsi la taille de l'image d'un carré, pour évaluer le grandissement.
Cette manipulation n'est pas facile. Vous pouvez commencer en plaçant la règle près de la lentille et en notant dans quel sens se déplace la règle observée directement, par rapport à la lettre vue à travers la lentille, lorsque vous vous déplacez vers la droite. Puis faire de même avec la règle assez loin de la lentille (50 cm environ).
// Le professeur conseille aux élèves de refaire l'expérience
chez eux avec une loupe.
// Les élèves trouvent |p| = 25 à 35 cm au lieu
des 22 attendus. La mesure avec une loupe est plus précise car celle-ci
a un plus grand diamètre.
Complétez le tableau suivant :
| y = 1/p' = 1/ |
||||||
| x = 1/p = 1/ |
Représentez graphiquement la relation qui à x fait correspondre y.
Déduisez en une relation entre les mesures algébriques
OA
et OA'.
Que représentent les points d’intersection C et D, de la courbe obtenue avec les axes de coordonnées ?
Déduisez de ceci les valeurs expérimentales des distances focales objet et image et de la vergence de la lentille L1.
La courbe traverse trois quadrants. Classez les en : image, objet, réel, virtuel.
pour la lentille convergente de 8 dioptries, dans un cas simple
:
Exemple : OA = -0,40m ; OA' = ; AB
= ; A'B' =
dans un cas simple, objet réel, image virtuelle.
Mesurez les valeurs algébriques OA et OA'.
Utilisez la loi de conjugaison pour en déduire une valeur de la
distance focale.
Calculez la vergence et comparez la à celle indiquée sur
la lentille.
Veuillez consulter la
leçon précédente, correspondant à l'ancien
programme, mais dans laquelle l'esprit du nouveau
programme est évoqué.
Formez l’image du paysage extérieur sur un écran en
essayant la loupe et les différentes lentilles. Au besoin, associez
plusieurs lentilles. Qu’en concluez-vous ? Mesurez la distance focale de
la loupe, d'une lentille.
// De cette étude, il doit ressortir que seules les lentilles convergentes donnent, dans ces conditions expérimentales, une image sur la feuille de papier. Certaines lentilles sont plus convergentes que d'autres ; elles donnent des images du paysage plus proches d'elles et plus petites. En accolant plusieurs lentilles convergentes, on obtient l'équivalent d'une lentille encore plus convergente.
Déduisez de vos expériences une relation qualitative
entre la position de l'objet lumineux et de son image. Masquez une partie
de la lentille : quelle est la conséquence sur l'image ?
// Il doit ressortir que l'objet et l'image se déplacent dans
le même sens, par rapport à la lentille (lorsque l'objet s'approche
de la lentille, l'image s'en éloigne). Lorsque l'objet se trouve
au niveau du foyer objet (symétrique du foyer image par rapport
à la lentille), l'image est à l'infini.
Quel nom donne-t-on à : A, A', O, AA' ?

1.4.1. Tout rayon incident parallèle à l'axe optique émerge en passant par le foyer image F'.1.4.2. Tout rayon passant par le centre optique n'est pas dévié.1.4.3. Tout rayon incident passant par le foyer objet F émerge parallèlement à l'axe optique |
// Non exigible au baccalauréat.
Ces lois se démontrent, à partir des précédentes
: (veuillez noter notre méthode peu orthodoxe de notation des mesures
algébriques)
Homothétie de centre 0 : g = A'B'
/ AB = A'B' / OB1
, avec OB1 = AB.
Et g = OA' / OA
Par l'homothétie de centre F',
g = A'B' / OB1
= F'A' / F'O d'où :
OA' / OA = F'A'
/ F'O = ( F'O + OA'
) / F'O soit en développant et divisant par OA'
, la loi de conjugaison en position.
Avec le banc d’optique, une lettre lumineuse et un écran,
étudiez la loi de conjugaison en position, avec une lentille convergente
de vergence 8 dioptries. Rappel : La vergence, mesurée en dioptries
(symbole d) est l'inverse de la distance focale
mesurée en mètres.

Pour un objet placé 40 cm avant la lentille (vous vous référez au sens de propagation de la lumière), cherchez plusieurs fois de suite la position de l’image. Quelle est votre conclusion ?
Réponse : Nous observons une latitude de mise au point. Nous prendrons le résultat moyen.
Remplissez le tableau de mesures suivant :
| p = |
-1,25 | -0,65 | -0,35 | -0,25 |
| p’ = |
Mesurez le grandissement dans l'un des cas.
Complétez le tableau suivant :
| y
= 1/p' = 1/ |
||||
| x = 1/p = 1/ |
Représentez graphiquement la relation qui à x fait correspondre
y.
Déduisez en une relation entre les mesures algébriques
OA
et OA'.
Que représentent les points d’intersection C et D, de la courbe
obtenue avec les axes de coordonnées ?
Déduisez de ceci les valeurs expérimentales des distances
focales objet et image et de la vergence de la lentille.
Nous devons définir un repère (O, i, j). En posant
p = OA, p ' = OA' et f ' = OF',
la relation entre les positions de l'objet et de son image s'écrit
:
- 1 / p + 1 / p ' = 1 / f ' |
g = |
// Non exigible au baccalauréat.
Pour obtenir une image nette, avec une lentille simple, il faut se
placer dans
les conditions de Gauss :
|
// Note : Les objectifs photographiques, formés de nombreuses lentilles, peuvent donner des images nettes, tout en ne respectant pas les conditions de Gauss.
Sur le Hachette :
Page 15 et suivantes : exercices 8, 9 (ajouter à la question
2.3. : Tracez la marche d'un faisceau lumineux, si un écran masque
la moitié basse de la lentille.), 10, 12.
Un miroir sphérique est une portion de sphère (ou
calotte sphérique) réfléchissante. On appelle centre
du miroir, le centre de la sphère ; c'est aussi le centre optique.
Le rayon de la sphère, ou rayon de courbure du miroir, est le double
de la distance focale de celui-ci.
Un miroir concave est convergent.
Tout rayon incident parallèle à l'axe optique est réfléchi en passant par le foyer principal F'.Tout rayon passant par le centre du miroir n'est pas dévié.Tout rayon incident passant par le foyer principal F' est réfléchi parallèlement à l'axe optique |
Exemple d'application, le rétroviseur. De quel type de miroir s'agit-il, plan, convexe, concave ?
Un microscope peut être sommairement décrit comme constitué
par :
L'objectif et l'oculaire étant modélisés par
des lentilles minces, nous pouvons suivre la marche des rayons lumineux
à travers le microscope :

L'objectif L1 donne de l'objet AB, une image A1B1,
très agrandie et renversée. Remarquez que pour cela,
il faut que le point A soit, avant l'objectif, à une distance
à peine supérieure à la distance focale f'1
de celui-ci.
Cette distance est réglée de manière que l'image A1B1 soit dans le plan focal objet de l'oculaire L2. Ainsi A1B1, se comporte comme un objet lumineux pour l'oculaire, qui se comporte lui-même comme une loupe. L'oculaire donne de l'objet A1B1, une image A2B2, de même sens que A1B1, située à l'infini, qui peut donc être observée par l'œil, sans que celui-ci accommode.
Les microscopes à usage biologique sont tous construits avec la même distance F'1 - F2, D, appelée intervalle optique ou interstice, et valant 16 cm.
Vous devrez savoir construire ces deux images graphiquement, calculer leurs caractéristiques en employant les lois de conjugaison et construire la marche d'un faisceau lumineux à travers le microscope.
Une grandeur plus pertinente, serait l'angle q',
sous lequel l'œil voit l'objet AB, à travers le microscope.
Prenons un exemple simple : Si nous observons une montagne haute de
1 km, à une distance de 10 km, ou une montagne de 2 km située
à 20 km, la taille sur notre rétine des 2 images sera la
même. Or cette taille est bien proportionnelle à l'angle q'.
Cet angle q', sous lequel est vu, à travers l'instrument d'optique, l'objet observé AB, est appelé le diamètre apparent de AB.
La figure précédente nous montre que |tan(q')| = A1B1 / f'2.
Si q', exprimé en radian, est petit, nous pouvons écrire : q' = A1B1 / f'2.
// Veuillez noter que cette approximation est habituelle en optique. Nous ne la justifierons pas plus, mais elle donne des résultats corrects.
// Vous devrez savoir utiliser et exploiter la définition
du grossissement, son expression vous étant donnée.
Une conséquence de ce que nous venons de voir dans le paragraphe
précédent, est que connaître le grandissement d'un
microscope n'offre aucun intérêt. Nous définissons
donc :
| Le grossissement standard d'un microscope est le rapport G = q' / q, où q' est l'angle sous lequel l'objet est vu à travers l'instrument d'optique, l'image étant formée à l'infini, et q est l'angle sous lequel l'objet est vu, à l'œil nu, à une distance de 25 cm. |
Exprimons le grossissement standard d'un microscope, en fonction des caractéristiques de celui-ci :
q = AB / 0,25 ; q'
= A1B1
/ f'2.
Exprimons A1B1
en fonction de AB en utilisant
une homothétie de centre F'1 : A1B1
/
AB = D / f'1.
Il vient finalement : G = D / (4 . f'1. f'2).
G peut aussi s'écrire : G = (A1B1
/ AB)
. (0,25 / f'2), soit
| G = Grandissement de l'objectif x Grossissement standard de l'oculaire. |
Valeurs qui sont gravées sur ces deux composants du microscope.
En effet, le grossissement standard de l'oculaire vaut : Goculaire
= a' / a, où
a'
est l'angle sous lequel l'objet est vu à travers l'oculaire, l'image
étant formée à l'infini, et a
est l'angle sous lequel l'objet est vu, à l'œil nu, à une
distance de 25 cm.
Or, pour un objet quelconque CD, observé à travers l'oculaire,
puis à l'œil nu, dans les conditions indiquées, nous pouvons
écrire : a' = CD / f'2
et a = CD / 0,25 ; donc Goculaire
= a' / a =
0,25 / f'2.
Posons-nous la question suivante : y a-t-il une zone de l'espace
particulière, par laquelle passent tous les rayons lumineux sortant
de l'oculaire du microscope ? Pourrions-nous la trouver sans calculs compliqués
?
Tous les rayons utiles (issus de l'objet observé et qui entrent dans le microscope) passent par l'objectif. Celui-ci étant assimilé à une lentille mince, tous ces rayons, avec des directions variées passent par le disque objectif. Seuls ceux de ces rayons qui atteignent l'oculaire ressortent du microscope. Ils repassent donc tous par un autre disque, image de l'objectif donnée par l'oculaire. Ce disque oculaire est situé juste après le foyer image de l'oculaire.
Autre démonstration : Soit 2 points lumineux
A et B d'un objet observé au microscope. Ils envoient dans celui-ci
deux faisceaux lumineux qui ont en commun le disque objectif. Deux rayons
lumineux, 1 issu de A, l'autre de B, qui frappent l'objectif en un même
point C ressortent du microscope en passant par C'', image de C donnée
par l'oculaire.
| Le cercle oculaire est l'image de l'objectif donnée par l'oculaire. |
C'est au niveau du cercle oculaire que l'observateur doit placer sa pupille. Il recevra le maximum de lumière.
// Note : Le diamètre du cercle oculaire est aussi important, à cause du phénomène de diffraction.
Banc d'optique, morceau de papier millimétré sur un
support, lampe de bureau munie d'une ampoule 15 watts, une boite de lentilles,
trois supports, un écran. Éventuellement, à la place
de la lampe de bureau, lanterne livrée avec le banc optique et calque
destiné à diminuer la quantité de lumière émise,
pour l'observation directe.
Sur le banc d'optique, placez le morceau de papier millimétré,
éclairé par la lampe de bureau ; à 30 cm environ de
celle-ci, une lentille de 8 dioptries qui constituera l'objectif du modèle
et à 62,5 cm de l'objectif, une lentille de 5 dioptries représentant
l'oculaire. Comme dans un microscope réel, cette distance
objectif, oculaire ne sera plus modifiée.
Reportez-vous à la figure suivante (la règle dessinée
à droite est inutile) :
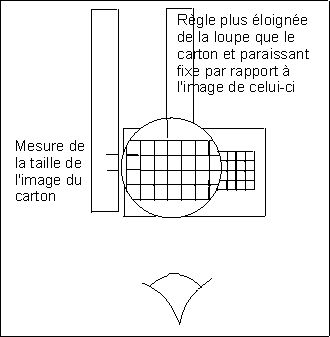
Lisez page 24 : Rechercher la position de l'objet.
Pages 25 et suivantes, exercices : 7, 9 (supprimez la question 3 et
ajoutez : Tracez un faisceau lumineux issu d'un objet situé sur
l'axe optique).
Nous pouvons modéliser une lunette astronomique à
l’aide de deux lentilles minces convergentes : un objectif de grande distance
focale, qui donne dans son plan focal image, une image du sujet visé
situé à l’infini ; et un oculaire, de courte distance focale
qui joue le rôle de loupe pour observer cette image.
En effet, un objet situé à grande distance, vu sous un
angle apparent q, donne une image d'autant plus
grande que la distance focale de l'objectif est grande. Par contre, plus
la focale de l'oculaire sera courte, plus cette image sera vue sous un
grand angle apparent.
L'objectif a un grand diamètre, pour collecter beaucoup de lumière.
Plaçons nous dans le cas le plus simple, lorsque l'œil de
l'observateur n'accommode pas. Un objet AB à l’infini donne une
image située dans le plan focal image de l'objectif. Cette image,
qui se comporte comme un objet lumineux pour l'oculaire, doit être
dans le plan focal objet de celui-ci, pour qu'il en donne une image à
l'infini.

Nous nous sommes placés dans le cas le plus simple où
F'1 et F2 sont confondus.
Finalement, avec cette lunette astronomique, un objet réel AB
à l’infini donne une image A2B2, renversée,
à l’infini. Les faisceaux parallèles à l’entrée,
inclinés de a sur l’axe optique, ressortent
parallèles, mais inclinés de a'.
La lunette est donc afocale.
Vous devrez aussi savoir tracer la marche d'un faisceau lumineux, à
travers la lunette.
| |G| = f'1 / f'2. |
| G = - f'1 / f'2. |
Toute la lumière collectée par l'objectif et sortant par l'oculaire, passe par le cercle oculaire ; la lunette est un collecteur de lumière.
Matériel nécessaire, pour chaque groupe : 1
lentille convergente de 3 d, 1 lentille convergente
de 8 d, 2 supports de lentilles, un banc d'optique
(il est possible de faire plus simple, avec une planchette).
Protocole : Nous allons réaliser une lunette astronomique
de faible grossissement. Placez à environ 20 cm d'une extrémité
du banc, une lentille de + 3 d, qui sera l'objectif.
Réalisez un oculaire de vergence + 8 d.
Où devez-vous le placer, pour que votre œil puisse observer un
paysage à l'infini, sans accommoder ?
Dans quel sens faudra-t-il déplacer l'oculaire, pour observer
un objet plus proche ?
Visez, à travers les 2 lentilles, un objet éloigné,
en posant le banc sur votre épaule, sans blesser vos camarades.
Ajustez la mise au point, puis évaluez le grossissement standard,
en visant un objet avec les deux yeux, un regardant à travers la
lunette, l'autre directement.
Calculez le grossissement standard, à partir des vergences des
lentilles employées. Comparez vos résultats.
Vous disposez de lentilles de + 2, + 3, + 8 d
; proposez la combinaison donnant le plus fort grossissement standard.
Nous pouvons modéliser un télescope de Newton à
l’aide d'un miroir concave (donc convergent) et d'une lentille mince convergente
: Le miroir est un objectif de grande distance focale, qui donne dans son
plan focal principal une image, du sujet visé situé à
l’infini ; la lentille est un oculaire, de courte distance focale qui joue
le rôle de loupe pour observer cette image. Pour permettre l'observation,
un miroir plan, incliné à 45°, renvoie sur le côté,
l'image donnée par l'objectif. Il est appelé miroir secondaire.
Vous devez savoir construire l'image donnée par le miroir
principal concave, convergent, d'un objet plan perpendiculaire à
l'axe optique ; cette image intermédiaire se comportant maintenant
comme un objet, savoir construire son image donnée par le miroir
secondaire plan (voir programme de 1° S) ; Cette dernière image
se comportant comme un objet pour la lentille convergente de l'oculaire,
savoir construire son image.
| |G| = f'1 / f'2. |
Considérons deux faisceaux de lumière pénétrant
dans le télescope, provenant de deux objets différents. Ils
ont en commun le disque du miroir concave (objectif). Ils ont donc aussi
en commun l’image de ce disque à travers le télescope. C’est
aussi l’image de l’objectif donnée par l’oculaire. On l’appelle
le cercle oculaire. Tous les rayons sortant du télescope
passent dans le cercle oculaire. C’est là qu’il faut placer la pupille
de l’œil.
Toute la lumière collectée par l'objectif et sortant par l'oculaire, passe par le cercle oculaire ; le télescope est un collecteur de lumière.
Matériel nécessaire, pour chaque groupe : 1
miroir sphérique concave, 1 miroir plan, 1 lentille convergente
de chacune des vergences suivantes : 2 d, 3
d,
8 d, 3 supports de lentilles, 1 pied de physique
supportant 1 planche à dessin format A3, placée en hauteur,
pour être au niveau de la fenêtre.
Protocole : Réalisation d'un télescope de Newton.
Placez le miroir sphérique dans son support (si vous disposez d'un
support permettant d'orienter vers le haut ou le bas l'objet qu'il maintient,
réservez-le à ce miroir sphérique), dans un coin de
la planche à dessin, de manière à obtenir une image
du paysage extérieur. Placez sur la planche, judicieusement, le
miroir secondaire plan, puis l'oculaire (5 d,
pour commencer).
Pour vous aider : Le miroir sphérique doit viser le paysage
extérieur. Placez le miroir secondaire sur le trajet des rayons
lumineux issus du miroir principal, entre celui-ci et l'image, à
45 °. Pour cela, regardez à l'œil nu dans le miroir secondaire,
et tournez-le pour apercevoir le miroir principal. En vous reculant, vous
devriez voir l'image du paysage extérieur (Si cela est possible,
orientez le plan du miroir principal un peu vers le ciel). Sans bouger
la tête, placez, entre le miroir secondaire et votre œil, l'oculaire
de 5 d, pour commencer. Faites la mise au point,
en approchant l'œil de l'oculaire et en déplaçant celui-ci.
Note : Un élève pose une excellente question : Comment se fait-il que le miroir secondaire ne "bouche pas la vue" du miroir sphérique ? L'expérience montrera que le miroir secondaire gêne l'observation, mais ne la rend pas impossible. Des rayons lumineux passent à côté.
Observez.
Essayez de reconnaître la partie du paysage extérieur
que vous apercevez.
L'image est-elle droite ou renversée ? Y a t-il grossissement
(> 1) ?
Vous disposez de lentilles de + 2, + 3, + 8 d.
Comment
augmenter le grossissement de ce télescope ?
Pages 38 et suivantes, exercices n° : 14 (Ajoutez : Comparez
le diamètre de ce cercle oculaire, à celui de votre pupille),
10.
Une proposition de travail pratique, plutôt adaptée à l'enseignement de MPI, est à trouver dans le chapitre Mesures Physiques et Informatiques. Elle utilise un logiciel, WaveFFT, gratuit disponible sur ce site (permettant la FFT, l'étude des séries de Fourier et le traçage de sonagrammes), livré une aide en ligne au format Html, et comporte un texte de travail pratique et divers fichiers sonores enregistrés à partir d'un piano droit, d'autres instruments, des sons générés par un synthétiseur, ainsi qu'un son donné par un récepteur radio accordé pour détecter le passage de météorites (un projet en cours, avec les collègues de sciences de la vie et de la Terre). Ce TP est bien trop long pour l'enseignement de spécialité, mais pourra donner des idées.
La notion de phase des harmoniques est hors programme et n'est donc pas traitée. Le logiciel WaveFFT permet cependant de retrouver celle-ci, en copiant les parties réelle et imaginaire de la FFT dans un tableur.
Elle comporte essentiellement (pour le physicien) :
Elle comporte essentiellement (pour le physicien) :
| Tous les instruments de musique comportent un système mécanique vibrant, associé à un système assurant le couplage avec l'air. |
Lieu : Si possible, salle informatique.
Matériel nécessaire : Masse à crochet, ressort. Diapason, sa caisse de résonance et marteau. Xylophone d'écolier. Flûte à bec (démontable) (une flûte traversière, avec son musicien serait préférable), corde tendue sur un support rigide (chevron ou planche, 1 ou 2 clous de fixation, 2 baguettes à section carrée en bois, 1 tige cylindrique en métal, 1 crochet, grosses masses marquées, de 5 kg..., 1 serre joint pour tenir la planche, ou un contrepoids de 1 kg), microphone, ordinateur muni d'une carte son, ou ordinateur avec carte d'acquisition, amplificateur et logiciel Synchronie (ou WinLabo...), logiciel WaveFFT, freeware disponible sur ce site.
Expériences :
Démonstration du phénomène de résonance,
par le professeur, à l'aide de la masse à crochet, suspendue
à un ressort : Excitation à une fréquence très
basse (que vaut l'amplitude du déplacement du centre de gravité
de la masse, que vaut sa vitesse ?), à la fréquence de résonance,
à une fréquence très élevée (que vaut
l'amplitude du déplacement, comparez déplacement de la main
et du centre de gravité de la masse à crochet).
Comparez le son émis par un diapason, sans sa caisse en bois, avec sa caisse bouchée à la main, puis débouchée, sans sa caisse et appuyé sur un support, en bois de préférence. Interprétez ces résultats.
Examinez (et écoutez) un xylophone. En quel matériau sont les lames ? Pourrait-on les réaliser en plomb ? Pourquoi ?
Enregistrez le son émis par le biseau bouché d'une flûte
à bec, le microphone étant placé dans l'axe, à
quelques centimètres de l'embouchure.
Retrouvez sa fréquence (s'il en a une), ou les fréquences
qui le constituent, à l'aide du logiciel WaveFFT ou d'un autre.
Enregistrez le son d'une note jouée par la même flûte,
en essayant de souffler avec la même force, le microphone étant
placé dans l'axe, à quelques centimètres de l'embouchure.
Trouvez sa fréquence, ou ses fréquences et son amplitude.
Comparez ces résultats aux précédents, concluez.
// Note : Des enregistrements de ces sons, sont disponibles sur ce site.
Faites vibrer une corde tendue sur un support rigide ; écoutez.
Recommencez, en appuyant ce support sur une table, de préférence
en bois.
Enregistrez le son obtenu, à l'aide d'un microphone ; observez
l'allure de la courbe représentant la tension en fonction de la
date. Effectuez une FFT, tracez un sonagramme. Quelles fréquences
comporte ce son.
Question : Comment faites-vous pour que votre voix porte plus loin ? Expliquez le rôle de vos mains dans ce cas.
// Réponse partielle : Seul, le biseau de flûte bouché ne produit pas une fréquence, mais un mélange de toutes les fréquences (un bruit ressemblant à du souffle, ou au son "che"). Le biseau associé à la flûte, produit des fréquences précises, avec une amplitude plus grande. Le corps de la flûte se comporte comme un résonateur.
Page 49 et suivantes, exercices : 5.1., 9.1., 9.2.
Le programme officiel recommande : "On ne s'intéressera
qu'aux vibrations transversales des cordes. En évitant d'exciter
la corde à une de ses extrémités, on travaille sur
la situation idéale d'une corde tendue entre deux points fixes.
On pourra à cette occasion réinvestir la force de Laplace
vue en première".
Expérience : Voir le travail pratique proposé au paragraphe 5.2.
Conclusion : Nous observons que :
Différentes techniques sont utilisables :
Matériel nécessaire (démonstration de cours)
: 1 corde métallique tendue sur un support rigide (chevron, clou
de fixation, poulie solide et son support, ou simplement un crayon servant
de frette), grosses masses marquées (5 kg, attention au risque de
chute sur un pied) , 1 ou 2 aimants en U (fort champ magnétique,
exemple aimants Leybold), 1 générateur basse fréquence,
2 prises BNC, fils, fils longs, 1 rhéostat de 10 ohms, 2 pinces
crocodile, 1 stroboscope, 1 microphone, 1 oscilloscope (à mémoire
éventuellement, avec module FFT), 1 boîte en bois (boîte
à produits) faisant "caisse de résonance" (un bureau en bois
fait aussi l'affaire), 1 amplificateur de puissance (et des câbles
de connexion, raccord bananes - prise CINCH, fils pour haut-parleur).
// Pour notre part, nous utilisons un amplificateur de
chaîne Hi-Fi pas trop coûteux, relié à la corde,
par l'intermédiaire d'un rhéostat de 4 à 10 ohms.
Il est parfois conseillé de choisir une corde
en matériau non magnétique, mais cela n'a pas grande importance
si le champ magnétique appliqué à la corde est uniforme,
créé par exemple par un aimant en U.
Protocole : Excitons une corde tendue, à différentes fréquences. Pour cela, un générateur basse fréquence délivrant un signal sinusoïdal (Level à mi course) est raccordé à l'entrée tuner d'un amplificateur haute fidélité. Il faut veiller à ne pas créer de courts-circuits à l'arrière de celui-ci, donc ne pas laisser traîner de matériel de physique. Le volume de l'amplificateur est réglé à mi course. La sortie (ne pas se tromper de voie) est raccordée à un rhéostat (supportant plusieurs ampères) d'environ 8 ohms, en série avec le fil métallique tendu. Attention, celui-ci devient brûlant !
| Numéro
de l'harm- onique |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| Fonda-
mental |
Octa
ve |
Octa
ve |
Octa
ve |
Octa
ve |
|||||||||||||||
| Note
approchée |
Do1 | Do2 | Sol2 | Do3 | Mi3 | Sol3 | La3 | Do4 | Ré4 | Mi4 | Fa4 | Sol4 | La4 | La#4 | Si4 | Do5 | Do#5 | Ré5 | Ré#5 |
Les haut-parleurs sont des modèles du genre HP 508 R, d'impédance 8 W et de puissance 0,3 W, vendus 0,42 euro (il ne faut pas s'en priver ; ils ne descendent pas très bas en fréquence, mais cela suffit). A basse fréquence, le générateur basse fréquence sera utilisé à assez forte puissance ; à fréquence plus élevée (2° harmonique), la puissance sera diminuée. Ces haut-parleurs pourront être maintenus en face de l'entrée du tube de Kundt, tout simplement par une masse marquée de 500 ou 1000 g, sur laquelle ils seront collés par les forces magnétiques.
Choisissez une longueur de colonne de 40 cm (Si vous avez un tube de
Kundt, vous n'avez pas le choix), avec le tube ouvert à l'extrémité
opposée au haut-parleur.
Recherchez les fréquences pour lesquelles le son émis
par la colonne est le plus fort.
Pour les 2 ou 3 premières fréquences trouvées,
cherchez avec le plateau et les graines (ou la poudre de lycopode) les
régions ou l'amplitude de vibration est la plus forte et celles
où elle est la plus faible.
Recommencez les mesures des 2 premières fréquences propres,
pour une longueur de 60 cm si vous disposez d'un tube à coulisse.
Avec le tube de Kundt, fermez le tube à l'extrémité
opposée au haut-parleur et réduisez sa longueur (de moitié),
pour retrouver les fréquences de l'expérience précédente.
Puis réduisez encore la longueur de moitié et retrouvez les
2 premières fréquences propres.
Une colonne d'air, soumise à des oscillations forcées, entre en résonance pour des fréquences particulières (discrètes ou quantifiées). La plus faible est le fondamental (ou premier harmonique), les autres, multiples du fondamental, sont les harmoniques. Les valeurs de ces fréquences propres sont fonction de la longueur de la colonne d'air.
Les molécules de la colonne d'air vibrent à des amplitudes différentes, nulles (nœuds d'amplitude) ou maximales (ventres d'amplitude). Il y a un ventre à l'entrée de la colonne et un à sa sortie, si la colonne est ouverte.
Page 49 et suivantes, exercices : 5.2., 5.3., 5.4., 6, 8.
Matériel nécessaire : 1 tuyau de caoutchouc (ancien
tuyau à gaz, ou feuille anglaise). 2 manipulateurs.
Expériences : Observer la réflexion de l'onde progressive transversale, sur l'extrémité fixe. Puis éventuellement sur l'extrémité tenue "souplement".
Observations : Lorsqu'une onde progressive se réfléchit sur un obstacle fixe unique, l'onde réfléchie est d'amplitude opposée à l'onde incidente. Elle se propage bien évidemment en sens inverse.
Interprétation qualitative : Soit une corde de longueur L, le
long de laquelle se propage une onde progressive, de la gauche vers la
droite. Pour décrire le phénomène de l'onde réfléchie,
vous pouvez imaginer que la corde a une longueur 2 L et que simultanément,
l'onde progressive est créée à son extrémité
gauche, allant de gauche à droite, et l'onde réfléchie
est créée à son extrémité droite, allant
de droite à gauche.
Ces deux ondes arrivent simultanément au point fixe, milieu
de cette corde imaginaire. Elles se superposent (s'ajoutent) ; donc pour
que le point reste fixe, il faut qu'elles soient d'amplitude opposée.
Matériel nécessaire : Cuve à onde, générateur
d'ondes rectilignes. Le stroboscope doit être à l'arrêt.
Protocole : Créez une onde linéaire de très
basse fréquence, de courte durée (train d'onde). Observez
sa réflexion sur un obstacle parallèle au "plan" d'onde (ou
à la source).
// Pour qu'on puisse parler d'onde stationnaire, les
2 ondes doivent avoir la même direction et des sens contraires.
Puis créez une onde progressive sinusoïdale. Remarquez que la superposition d'une onde incidente et d'une onde réfléchie donne une onde stationnaire. Pour cela, augmentez la fréquence, jusqu'à ce que les ondes progressives ne soient plus visibles pour un observateur immobile. Elles sont encore visibles si l'observateur stroboscope, soit en déplaçant rapidement la tête, soit en agitant sa main, doigts écartés, devant ses yeux. La position naturelle des doigts est parallèle à l'image des fronts d'onde. Si les doigts sont placés perpendiculairement aux fronts d'onde, soit dans la direction de propagation, la stroboscopie incline les fronts d'onde. C'est un phénomène connu des photographes qui enregistrent avec un obturateur à rideaux (appareil réflexe) un objet en mouvement rapide. Placez alors le réflecteur. Faites remarquer qu'il n'est plus nécessaire de stroboscoper pour observer des traits fixes, alternativement brillants et sombres. Il s'agit d'ondes stationnaires. Stationnaire ne signifie pas qu'il n'y a pas mouvement des particules dans l'eau, mais qu'il ya des noeuds et des ventres de vibration (Cela apparaîtra plus clairement dans la simulation informatique).
// Le professeur pourra tricher un peu, en se plaçant
sans le dire, près d'une condition de résonance.
Une onde stationnaire est une onde qui ne se propage plus (il est inutile
de stroboscoper pour l'observer).
En diminuant à nouveau la fréquence, il devrait être
possible d'observer que certaines zones d'amplitude de vibration nulle
(noeuds) paraissent grises (et fixes) ; celles d'amplitude de vibration
maximale (ventres) paraissent alternativement sombres puis claires ; elles
sont situées au milieu des noeuds.
Interprétation qualitative : Deux ondes sinusoïdales se propagent en sens inverse. Dans certaines zones situées en des endroits précis et fixes, elles sont toujours d'amplitude opposée (elles sont en opposition de phase) ; par superposition, leurs effets s'annulent : Ces zones ont une amplitude de vibration nulle (nœuds de vibrations). Dans d'autres zones, les effets (tantôt dans un sens, tantôt dans l'autre) s'ajoutent toujours (elles sont en phase) ; ces zones ont une amplitude de vibration maximale (ventres de vibration) qui est le double de l'amplitude de l'onde progressive.
Vous trouverez sur Internet de nombreux exemples de simulations
d'ondes, réalisés parfois par des Universités. Mais
généralement, ils demandent de rester en ligne pour fonctionner.
Voici une modeste simulation que j'ai réalisée en Delphi 5, à l'aide du composant graphique TChart. Elle est livrée avec son code source, pour amélioration, et une aide. Elle peut lire des fiches de travaux pratiques au format RTF.
Observez la propagation et la réflexion d'une impulsion. Vous pouvez choisir
Observez la propagation, puis la réflexion sur 2 obstacles fixes,
d'une onde sinusoïdale progressive. Veuillez noter que l'onde progressive
initiale a une amplitude 6 fois plus faible
que dans le cas précédent.
Remarquez que dans le cas quelconque, les ondes seront brouillées
(cela ne se voit pas ici, car l'animation est trop lente ; il faut imaginer
ce qui se passerait en accéléré).
Dans le cas de la résonance, notez que l'amplitude de l'onde
stationnaire augmente et devient très supérieure à
celle de l'onde progressive initiale.
// Remarque : Ces 2 dernières simulations sont approximatives.
Rappelons que la longueur d'onde l est
la distance parcourue pendant une période T. l
= v . T, ou l = v / n,
où v est la célérité de l'onde et n
sa
fréquence.
| Lorsqu'une onde progressive sinusoïdale incidente se superpose à l'onde réfléchie, il se produit une onde stationnaire. La longueur d'un fuseau, ou la distance entre 2 nœuds consécutifs est égale à la demi longueur d'onde, l / 2. De même pour la distance entre 2 ventres. |
Pour certaines distances particulières, séparant l'émetteur
d'ondes progressives du miroir, nous observons que les ondes stationnaires
sont bien marquées.
L'onde progressive, limitée dans l'espace par
les 2 obstacles fixes séparés par une distance L, se réfléchit
de multiples fois. Onde1 et onde2 se superposent en donnant des nœuds de
vibrations situés à des distances k . l
/ 2 de l'obstacle de droite. Onde2 et onde3 se superposent en donnant des
nœuds de vibrations situés à des distances k . l
/ 2 de l'obstacle de gauche. En général, cela conduit
à une figure brouillée. Sauf si tous les nœuds se superposent,
ce qui impose L = n . l / 2, n étant
un nombre entier. Les amplitudes de vibration au niveau des ventres, sont
alors augmentées par la superposition : il s'agit d'un phénomène
de résonance.
Autre raisonnement : Les ondes onde1 et onde3, ainsi que onde2 et onde4 doivent être en phase. Or, de onde1 à onde3, la distance parcourue est 2 . L. Donc 2 . L = n . l.
Une onde progressive qui se réfléchit sur 2 obstacles
fixes donne une onde stationnaire (des nœuds de vibration nulle, et des
ventres marqués de grande amplitude de vibration par un effet de
résonance) si la relation
| 2 . L = n . l |
ou L = n . l / 2,
est vérifiée, où L est la distance en mètre
entre les 2 obstacles, n est un entier positif, l
est la longueur de l'onde en mètre.
Cette relation peut aussi s'écrire :
| n = n . v / 2L. |
Où n est la fréquence de l'onde progressive en Hz, et v sa célérité en m . s-1.
Note : La célérité d'une onde progressive, dans une corde tendue (parfaitement souple) est donnée par la relation :
v = racine carrée (F / m), où
F est la tension de la corde en newton et m,
sa masse linéique en kg . m-1. La masse linéique
est numériquement égale à la masse d'1 mètre
de corde. Cette relation n'est pas à savoir ; elle vous sera donnée
au baccalauréat, si besoin est.
| Les modes de vibration entre 2 obstacles fixes sont quantifiés. Les différentes valeurs de n sont les fréquences propres. |
| La longueur d'un fuseau, ou la distance entre 2 nœuds consécutifs est égale à la demi longueur d'onde, l/ 2. De même pour la distance entre 2 ventres. |
Nous avons vérifié expérimentalement qu'aux
2 extrémités ouvertes d'une colonne d'air, se trouve un ventre
de vibration. Cela conduit à la même conclusion :
| Les modes de vibration d'une colonne d'air sont quantifiés. Les différentes valeurs de n sont les fréquences propres. |
| La distance entre 2 nœuds consécutifs est égale à la demi longueur d'onde, l / 2. De même pour la distance entre 2 ventres. |
Page 61 et suivantes. Lire l'exercice corrigé : Le tube de
Kundt. Exercices 4, 5, 8 (trombone de Koenig).
// Note : Le lecteur pourra consulter avec
profit l'article : "BOUYRIE, Guy. Jeux d'orgues. Bulletin de l'Union des
Physiciens. Décembre 2002, n° 849, p.1675. Article qui évoque
entre autres l'emploi du logiciel GoldWave, que vous pourrez trouver sur
Internet. Il trouvera des informations
complémentaires dans le chapitre MPI de ce site.
Matériel nécessaire : 1 générateur
basse fréquence, éventuellement, mais pas indispensable,
1 amplificateur haute fidélité, 1 prise BNC et cordon de
raccordement CINCH, 1 enceinte acoustique haute fidélité
(ou de bonne qualité), 1 sonomètre, 1 voltmètre numérique.
Précautions expérimentales : Si vous
décidez d'employer un amplificateur haute fidélité,
il faudra veiller à ne pas provoquer de court-circuit à l'arrière
de l'amplificateur, donc ne pas laisser traîner de matériel
de physique sur la paillasse (je sais de quoi je parle !) ; il ne faudra
pas envoyer une puissance trop forte dans l'enceinte acoustique, dans les
fréquences aiguës. En effet, lorsqu'une enceinte est donnée
comme capable de supporter une puissance de 50 W (par exemple), c'est à
condition que cette puissance soit répartie correctement dans tout
le spectre sonore, en respectant la répartition statistique en puissance
de la musique classique. Cette précaution paraît d'ailleurs
évidente si on considère la taille des moteurs des différents
haut-parleurs. Sachez que les éventuelles garanties à vie
de certaines enceintes haut de gamme, ne sont valables que si ces conditions
sont respectées (le critère étant de respecter la
puissance maximale admissible, avec une répartition spectrale de
puissance identique à celle de la musique classique, nettement
moins riche en fréquences aiguës que les musiques d'origine
électronique).
| Intensité sonore estimée à l'oreille | I | 2 I | 4 I | 8 I | 16 I | 32 I | 64 I | 128 I | 256 I |
| Niveau sonore L mesuré à l'aide d'un sonomètre, en dB | 66,3 | 69,2 | 72,8 | 75,9 | 78,2 | 80,5 | 83,4 | 86,5 | 88,6 |
| Tension efficace appliquée au haut-parleur, en mV | 12 | 17 | 27 | 40 | 55 | 73 | 106 | 155 | 201 |
Entre 2 mesures successives, la tension appliquée est multipliée en moyenne par racine huitième de 201 / 12, soit 1,42 (valeur théorique racine carrée de 2, soit 1,414) et l'intensité sonore augmente de (88,6 - 66,3) / 8 = 2,8 dB (valeur théorique 3 dB). La sensation sonore croît donc comme le carré de la valeur efficace de la tension appliquée au haut-parleur, elle- même proportionnelle à l'amplitude du déplacement de la membrane (voir loi F = k . I de l'ancien programme de seconde).
La sensation sonore est donc proportionnelle à la puissance émise par le haut-parleur (et dépend de la distance à celui-ci), si nous admettons que la puissance émise est proportionnelle au carré de l'amplitude du déplacement de la membrane, elle-même proportionnelle à l'amplitude de la tension appliquée. Une autre façon de parvenir à cette conclusion est d'admettre que pour une fréquence donnée (ici 440 Hz), la puissance sonore émise et l'intensité sonore reçue en un point de la salle, sont proportionnelles au produit U . I, ce qui revient à admettre que le haut-parleur se comporte comme une "résistance", en fait une impédance.
// Note : Certains ouvrages proposent pour doubler avec certitude l'intensité sonore reçue par chacun des élèves d'alimenter avec le même signal 2 haut-parleurs identiques. Cela est très contestable, pour les raisons suivantes : Si les mouvements des 2 membranes des haut-parleurs sont identiques, dans les régions où ces 2 signaux sont reçus en phase, la puissance reçue ne sera pas 2, mais 4 fois plus grande. En effet, les 2 amplitudes s'ajoutent, l'amplitude reçue est doublée et la puissance, proportionnelle au carré de l'amplitude, quadruple. Dans les zones où les 2 signaux sont reçus en opposition de phase, la puissance perçue sera nulle. Il faudrait disposer de 2 sources identiques, mais non cohérentes, par exemple 2 violons jouant la même note, avec la même force. Le problème est physiquement le même que lors de la superposition d'ondes lumineuses, selon qu'elles sont ou non cohérentes.
Conclusions : L'oreille humaine perçoit les sons de fréquences
comprises entre 20 et 20000 Hz (environ).
Remarquez que lorsque la puissance sonore reçue diminue, le
domaine des fréquences audibles se restreint. (Audiogramme).
A chaque fois que la puissance sonore émise double, notre perception sonore augmente de la même manière (fonction linéaire).
Le seuil d'audition, intensité sonore la plus faible que
l'oreille humaine puisse percevoir est I0 = 10-12
W . m-2. Il s'agit d'une puissance de 10-12 W, répartie
sur une surface de 1 mètre carré. Elle est prise comme intensité
de référence.
Par définition, le niveau sonore L est donné par la relation
:
| L = 10 . log10 (I / I0). |
| L en dB | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 |
| intensité sonore en
W . m-2. |
10-12 | 10-10 | 10-8 | 10-6 | 10-4 | 10-2 | 1 | 100 |
| Effet | reposant | fatigant | dangereux | douloureux | ||||
| Exemple | désert | conversation | avion |
Voici une phrase, trouvée dans un livre de terminale scientifique et qui me pose problème : "Le physiologiste allemand Fechner a observé que généralement les sensations physiologiques sont proportionnelles aux logarithmes des excitations physiques. C'est approximativement vrai pour l'ouïe." Or les mesures précédentes montrent, semble-t-il, que la sensation physiologique est proportionnelle à l'intensité sonore, elle même proportionnelle à la puissance émise par le haut-parleur, elle-même proportionnelle au carré de l'amplitude de déplacement de sa membrane, et donc au carré de l'amplitude de la tension appliquée, si l'auditeur ne change pas de position par rapport à la source sonore.
Notez, pour votre usage personnel, que beaucoup trop d'utilisateurs d'appareils musicaux portables, ont tendance à les employer à des intensités sonores trop élevées. La raison est que ces appareils, dotés uniquement d'écouteurs, ne peuvent faire vibrer notre cage thoracique, comme le font les sons graves produits par d'autres moyens (d'où les super basses et autres artifices). Ils sont responsables de nombreux cas de surdité. De même que certains concerts où la puissance sonore couvre la médiocre musicalité. Une oreille interne détruite ne peut être réparée. Elle peut être la cause d'acouphènes, sifflements permanents extrêmement pénibles. N'hésitez-pas à porter plainte contre les groupes musicaux dépassant les niveaux sonores dangereux, ou mieux, fuyez-les.
// Note : Le programme officiel place dans
les compétences exigibles, savoir-faire expérimentaux, pour
le baccalauréat : "Acquisition et analyse d'une note produite par
un instrument de musique". La difficulté va consister à gérer
le temps et le travail de groupe.
Acquisition par oscilloscope ou carte d'acquisition
et logiciel Synchronie, matériel nécessaire : 1 instrument
de musique, 1 microphone, 1 raccord microphone - système d'acquisition
(pinces crocodiles, ou adaptateur jack...), 1 système d'acquisition
(oscilloscope numérique, muni d'un module FFT, cher et rare, ou
carte d'acquisition et logiciel Synchronie, ce dernier nécessitant
l'emploi d'un amplificateur...).
Protocole, pour le logiciel Synchronie : Le paramétrage
se fait par : Paramètres | Réglage des paramètres
| onglet Acquisition, puis choix du nombre de points, de la Durée
par Échantillon, où un clic fait apparaître les différentes
unités possibles, ms, ms... Validez.
Puis faites : Exécuter | Acquérir signaux, puis enfin : traitements
| Analyse de Fourier | Signal à analyser | choisir le signal | Calculer,
mais auparavant, il aura fallu faire : Analyse de Fourier | Options avancées
| Aspect du tracé | Style des spectres | _____ | Calculer. En effet,
ne pas relier les points du spectre en fréquences, comme le fait
par défaut Synchronie, induit en erreur, les bâtonnets qu'il
trace ne correspondant en rien à des fonctions de Dirac, ou plus
simplement des harmoniques. Pour ceux que cela intéresse, j'indique
à la fin de cette leçon comment transférer
des fichiers Wave dans Synchronie.
Acquisition par la carte son de l'ordinateur, matériel nécessaire : Logiciel (graticiel) WaveFFT et fichiers sonores au format .wave, disponibles sur ce site, ordinateur. Pour acquérir vous-même des sons : 1 instrument de musique, 1 microphone, 1 raccord microphone - ordinateur (par exemple, raccord gros Jack, petit Jack). Pour enregistrer des sons, il est préférable de disposer d'une carte son de marque Sound Blaster et des excellents logiciels livrés avec. Un mode d'emploi détaillé figure sur ce site.
Mode d'emploi très succinct du logiciel WaveFFT : Chargez un son au format .Wave (1 seul canal à la fois). Pour effectuer une FFT, sélectionnez le nombre total de points, le numéro du point de départ, un éventuel saut de points. Un rectangle entoure alors la zone soumise à la FFT.
Vous disposez d'un enregistrement effectué dans les conditions suivantes : Un récepteur radio, doté d'une antenne directive, pointe dans la direction d'un émetteur en modulation de fréquence trop lointain pour être reçu. Car dans cette gamme de fréquences, les ondes électromagnétiques se propagent en ligne droite, et ne peuvent donc suivre la courbure de la Terre. Nous enregistrons donc du bruit (souffle). Par instants, des météorites traversent l'atmosphère, l'ionisent et ces segments de droite ionisés se comportent comme des antennes réémettrices. Un son musical est alors brièvement perçu.
Écoutez le fichier sonore radioFM.wav, puis tracez son sonagramme. Distinguez à l'oreille, puis sur le sonagramme, les brefs instants où de la musique est reçue. Les sonagrammes peuvent être transférés dans tout logiciel de dessin, par Copier | Coller.
// Note : Tracer un sonagramme consiste à prélever des tranches temporelles du son, puis à analyser les fréquences contenues dans chaque tranche. L'axe des x, est l'axe des dates successives des tranches sonores. Selon l'axe des ordonnées sont représentées les fréquences contenues dans les tranches. Les fréquences correspondant à de fortes amplitudes sonores sont en couleurs claires, les autres en couleurs sombres.
Notez que cette distinction son musical, bruit, comporte aussi des aspects culturels. Les instruments à percussion ont longtemps été bannis de la musique classique européenne, car considérés comme barbares. Au 19° siècle, la musique de Berlioz a fait scandale.

Sonagramme, passage de météorites.
Protocole : Fichier RadioFM.wav, amplification 45, point de départ 0, garder 1 point sur 2, FFT sur 1024 points, avance entre 2 FFT 128 points, fenêtre de Hamming, échelle linéaire.
| La4, flûte à bec
fenêtre de Blackman-Harris |
La4, flûte à bec
fenêtre rectangulaire |
La4, flûte traversière
Blackman-Harris |
 |
 |
 |
Voici 2 sonagrammes du La4 d'une flûte à bec, réalisés avec une fenêtre de Blackman-Harris et une fenêtre rectangulaire. Et 1 sonagramme du La4 d'une flûte traversière, réalisé avec une fenêtre de Blackman-Harris.
Vous remarquez les artefacts apportés par la fenêtre rectangulaire. La flûte à bec produit essentiellement des harmoniques de rang impair, la traversière tous les harmoniques. Notez que les images ci-dessus ont été obtenues avec une vieille version du logiciel WaveFFT.exe.
Protocole : Flûte à bec, La 4, fichier nommé par les élèves et par erreur FluteaBecLa3.wav, amplification 200, point de départ 0, garder 1 point sur 2, FFT sur 1024 points, avance entre 2 FFT 128 points, fenêtre de Blackman-Harris, ou fenêtre rectangulaire, échelle linéaire ou logarithmique.
Flûte traversière, La 4, fichier nommé FluteTraversièreLa4.wav, amplification 80, point de départ 0, garder 1 point sur 2, FFT sur 1024 points, avance entre 2 FFT 256 points, fenêtre de Blackman-Harris.
Spectres en fréquence
Comparez les spectres en fréquence de la note La3, jouée par un diapason, un piano ou un violon. Notez les fréquences du fondamental (appelé aussi premier harmonique) et des (autres) harmoniques.
Vous pouvez télé charger 3 copies d'écran, obtenues à l'aide du logiciel WaveFFT, disponible sur ce site :
La 3 d'un diapason,
la 3 d'un piano, la 3 d'un violon.
Chaque fichier a une taille d'environ 80 kilo octets.
| Nous constatons que 2 sons qui sont de même hauteur, ont la même fréquence fondamentale. |
Ces 2 sons ont donc la même "période", mais des évolutions
différentes dans chaque période.
// Note : Les sons produits par de "vrais" instruments, ne sont
souvent qu'approximativement périodiques.
| Les harmoniques sont différents. |
| Les transitoires d'attaque et d'extinction sont différents. |
Pour vous en convaincre, écoutez un son d'instrument qui a été simplement inversé temporellement, par exemple le fichier Do3inverse (disponible sur ce site, dans les sons de piano), qui est un Do3 de piano, dont les échantillons ont été retournés temporellement. Un son de piano inversé fait penser à un son d'accordéon. Pourtant, ces 2 sons comportent exactement les mêmes fréquences.
Vous pouvez effectuer ce retournement, avec un son de votre choix, par exemple à l'aide de l'excellent logiciel d'acquisition de sons, WaveStudio, livré avec les cartes son pour PC, Sound Blaster. Avec les anciennes cartes hélas, mais plus avec les récentes.
Vous n'aurez pas le temps de réaliser de travail en classe,
mais les plus motivés d'entre vous pourront l'effectuer chez eux.
Mesurez avec le maximum de précision les fréquences du fondamental
et du dixième harmonique du Do 3 d'un piano. Fichier Do3Long, FFT
sur 16 384 points, point de départ 1 600, garder 1 point sur 2.
La
fréquence du 10° harmonique suit-elle la loi énoncée
en cours ? Quelle peut en être la raison ?
// Réponse : Fondamental à 261,1
Hz, harmonique 10 (le 9° n'est pas visible) à 2664,3 Hz, donc
un peu trop aigü. C'est dû à la raideur des cordes du
piano.
Nous allons écouter et analyser des fragments sonores, enregistrés
sur l'ordinateur.
Il s'agit d'un extrait de Do3 de piano (Un enregistrement du piano
du professeur, malheureusement pas parfaitement accordé). La première
partie du son se nomme l'attaque. Le son est-il périodique lors
de l'attaque ?
Le son est-il rigoureusement périodique ? Est-il à
peu près périodique ?
Mesurez sa "période".
Pour cela, plusieurs méthodes sont possibles :
// Note : Il n'est pas prévu d'expliquer ici la théorie des transformations de Fourier. Si votre logiciel comporte le menu Démonstration, vous y trouverez les explications et formules mathématiques employées.
Quelle est la relation entre les fréquences de deux notes
séparées par une octave ?
Quelle est la fréquence du La3 ? Quelle doit-être celle
du La4 ?
Transférez dans Excel, le nom et la fréquence des
notes du Do3 au Do4.
Construisez une représentation graphique. La courbe obtenue
semble-t-elle régulière ?
Si non, pourquoi ?
Recommencez, en sautant une ligne pour chaque note manquante dans l'octave,
Do#, Ré#...
Choisissez un graphique formé de points.
Ajustez la série de points obtenus, par diverses fonctions.
A chaque fois, notez l'expression numérique de la fonction,
la valeur du coefficient de détermination. Notez aussi si la courbe
ajuste bien les points ou pas.
Quelle est la fonction qui ajuste le mieux les points (le coefficient
est le plus proche de 1) ?
Nous constatons que la fonction polynôme du second degré
ajuste très bien les points de mesure. Or cette fonction est représentée
par une parabole. Cela n'a pas de sens.
La fonction polynôme de degré 5 ajuste même parfaitement
les points. Cela a encore moins de sens.
// Notez que la représentation d'une fonction polynôme
de degré n peut passer exactement par n + 1 points donnés.
| Do 3 | 262,4 | 261,6 |
| Ré 3 | 293,1 | 293,7 |
| Mi 3 | 327,4 | 329,6 |
| Fa 3 | 348,9 | 349,2 |
| Sol 3 | 392,0 | 392,0 |
| La 3 | 439,3 | 440 |
| Si 3 | 493,1 | 493,9 |
| Do 4 | 525,6 | 523,3 |
Dans la gamme tempérée, en usage dans les pays occidentaux,
on passe d'une note à celle située un demi ton au-dessus,
en multipliant sa fréquence par la raison racine douzième
de 2, ou 2 1/12.
Ce choix permet
Page 73 et suivantes, exercices : 6 (audiogramme), 7, 8, 12 (difficile)
(niveau sonore), 10 (période, son pur), 11 (harmoniques), 13 (synthèse
de Fourier d'un créneau), 14 (harmoniques, FFT).
Ni Excel, ni Synchronie, ne savent lire les fichiers
Wave, pourtant bien pratiques. Le logiciel WaveFFT, disponible sur ce site,
peut lire de tels fichiers (ne soyez pas pressé), et les convertir
en un format texte, pour Mathematica ou Maple. Excel est capable de lire
au moins l'un des deux types. Une fois dans Excel, vous ferez Copier, puis
dans Synchronie, Tableur | Édition | Coller comme nouvelle variable.
Repérez le nom donné à la colonne de valeurs, repassez
dans le mode courbe, faites Paramètres | onglet Courbes | dans la
boîte de choix déroulante, choisir le nom correct | Fenêtre
-> 1 | OK.