Cours de première S, deuxième page
Page modifiée le 7 / 2 / 2007
Contenu : Forces, travail et énergie
: 6 Travail et puissance d'une force constante
; 7 énergie cinétique ; 8 énergie
potentielle
; 9 transferts d'énergie. Électrodynamique
: 10 Transferts d'énergie
dans un circuit électrique, générateurs et récepteurs
; 11 circuit électrique ; 12 champ
magnétique
; 13 Champ magnétique créé par un courant
; 14 forces électromagnétiques
Programme officiel
Le B.O. N°7, 31 AOÛT 2000
B - TRAVAIL MÉCANIQUE ET ÉNERGIE
Objectifs
Le but est d’introduire une grandeur fondamentale, l’énergie,
dont la conservation constitue une des lois les plus générales
de la physique et constitue le guide sous-jacent à la progression.
Différentes formes d’énergie sont introduites à
partir de la notion du travail d’une force, tout en montrant que selon
les situations, ces différentes formes sont susceptibles de se transformer
les unes dans les autres. L’objectif est ainsi de progresser vers l’idée
de conservation.
Enfin pour illustrer le fait que le travail n’est pas le seul mode
de transfert d’énergie, on termine cette introduction par quelques
considérations simples sur le transfert thermique, en évitant
la confusion entre chaleur et température.
| EXEMPLES D’ACTIVITÉS |
C O N T E N U S |
CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES |
Identifier les effets sur un solide de forces dont les points d’application
se déplacent dans le référentiel d’étude :
- modifications de la valeur de la vitesse d’un solide en chute libre,
d’un solide glissant sur un plan incliné, de la valeur de la vitesse
de rotation d’un solide autour d’un axe fixe, modifications de l’altitude,
de la température, de l’aspect...
Utiliser un tableur et un grapheur.
Étude quantitative des variations de la valeur de la vitesse
d’un corps dans différentes situations *
- chutes libres avec et sans vitesse initiale
(utilisation de capteurs chronocinés, de logiciels, de vidéos...)
;
- satellites en mouvement circulaire uniforme ;
- solide lancé sur une table...
Analyse du travail de la force de gravitation qui s’exerce sur
une comète;
conséquence sur sa vitesse.
Expérience de Joule ou équivalente.
Approche qualitative de la mise en contact de deux corps à des
températures différentes : évolution vers l’équilibre
thermique.
Analyse qualitative des transferts d’énergie se faisant sur un
système déterminé.
|
1 - Travail d’une force
1 . 1 Notion de travail d’une force
Effets possibles d’une force dont le point
d’application se déplace.
1. 2 Travail d’une force constante
WA B = F . A B = F.AB. cos a
Unité de travail : le joule (symbole: J).
Expression du travail du poids d’un corps. Travail moteur, travail
résistant.
1 . 3 Puissance du travail d’une ou plusieurs forces
2 - Le travail : un mode de transfert de l’énergie
2 . 1 Travail et énergie cinétique : Dans un référentiel
terrestre, étude expérimentale de la chute libre d’un corps
au voisinage de la Terre ; travail du poids :
WA B(P) = D[ (1/2) M VG2]
.
Interprétation énergétique ; définition
de
l’énergie cinétique d’un solide en translation.
Généralisation : pour un solide en translation soumis à
diverses forces : (1/2) M VB2 - (1/2) M VA2
= S WA B(Fe x t) .
2 . 2 Travail et énergie potentielle de pesanteur
Énergie potentielle d’un solide en interaction avec la
Terre ; Cas particulier des situations localisées au voisinage de
la Terre.
Relation Ep p = M g z .
Transformation d’énergie potentielle en énergie cinétique
dans le cas de la chute libre.
2 . 3 Travail et énergie interne
Quelques autres effets du travail reçu (déformations
élastiques, élévation de température, changements
d’état physico-chimiques). Notion d’énergie interne.
3 - Le transfert thermique
Un travail reçu peut produire une élévation de
température d’un corps. Une élévation identique de
température peut être obtenue par transfert d’énergie
sous une autre forme : le transfert thermique ; aspect microscopique.
Autre mode de transfert énergétique :
le rayonnement. |
Connaître quelques effets sur un solide de forces
dont le ou les points d’application se déplacent.
Exprimer et calculer le travail d’une force constante .
Savoir que le travail d’une force constante effectué entre deux
points A et B est indépendant du chemin parcouru.
Utiliser la relation P = W / Dt
Utiliser l’expression de l’énergie cinétique d’un solide
en translation.
Mettre en œuvre un dispositif décrit.
Utiliser le fait qu’entre deux positions, dans un référentiel
galiléen, la variation de l’énergie cinétique
d’un solide en translation est égale à la somme des travaux
des forces extérieures.
Utiliser l’expression de l’énergie potentielle de pesanteur
d’un solide au voisinage de la Terre.
Expliciter la transformation d’énergie potentielle en énergie
cinétique dans des cas simples.
Savoir que l’énergie reçue par travail peut aussi être
“stockée” par un corps dont certaines propriétés physiques
ou chimiques sont modifiées.
Savoir qu’à l’échelle macroscopique, un transfert
thermique se fait spontanément du système dont la température
est la plus élevée vers celui dont la température
est la plus basse.
Prévoir sur des exemples simples le sens d’un transfert thermique.
Savoir que le rayonnement est un mode de transfert de l’énergie.
|
La conclusion de l’analyse présentée
dans le chapitre s’exprimera sous la forme suivante :
À tout système dans un état donné, on peut
associer une grandeur appelée “énergie”. Si l’énergie
d’un système augmente ou diminue, c’est qu’il a reçu ou cédé
de l’énergie, que ce soit par travail, par transfert thermique ou
par rayonnement.
* Activités pouvant donner lieu à l’utilisation des technologies
de l’information et de la communication
Commentaires
Travail d’une force
Partant d’exemples concrets de la vie quotidienne, on constate que
des objets soumis à une force dont le point d’application se déplace
peuvent :
- être mis en mouvement (chariot, wagon, brique glissant sur
une table, etc.),
- changer d’altitude (bagage que l’on monte à l’étage),
- voir leur température s’élever,
- se déformer temporairement ou définitivement.
Dans tous ces cas, on dira que la force travaille.
On définit le travail WA B d’une force constante
F pour un déplacement A B de son point d’application par la relation
: WA B = F. AB = F.AB.cos a
Pour un solide en translation, tous les points du solide ont même
déplacement; le travail de forces réparties est alors identique
à celui de leur résultante.
Les forces de pesanteur (champ localement uniforme) sont équivalentes
à une force unique appliquée au centre d’inertie. Les altitudes
z étant mesurées sur un axe Oz vertical dirigé vers
le haut, on montrera que leur travail sur un solide s’exprime par WA
B = Mg (Z A - Z B ) lorsque le centre d’inertie
passe de l’altitude Z A à l’altitude Z B et
qu’il est indépendant du chemin suivi.
Travail et énergie cinétique
On part ici de situations concrètes permettant d’étudier
les effets d’une force extérieure sur la valeur de la vitesse du
centre d’inertie d’un solide en translation, en particulier l’influence
de la direction de la force par rapport à la direction du vecteur
vitesse (étude de la chute libre d’un solide sans vitesse initiale,
étude de la chute libre avec vitesse initiale vers le haut durant
la montée ou d’un mouvement de projectile, étude du mouvement
circulaire d’un satellite, étude d’un solide lancé et s’arrêtant
sur un plan horizontal, etc.).
L’idée est de chercher s’il existe une relation entre la valeur
de la vitesse du centre d’inertie du solide et le travail des forces extérieures.
Cette relation est d’abord introduite par le calcul du travail du poids
dans le cas de la chute libre d’un corps au voisinage de la Terre. On interprète
de façon énergétique cette relation de la façon
suivante : le travail du poids a servi à faire varier la vitesse
du solide. On définit l’énergie cinétique d’un solide
en translation par la relation 1 / 2. M VG 2 ; l’énergie
cinétique est donc une grandeur caractéristique de son état
de mouvement.
Cette relation est ensuite généralisée à
d’autres exemples simples, où d’autres forces que celle de pesanteur
agissent.
Pour un solide en translation, la somme des travaux des forces extérieures
S
WA B(Fe x t) est aussi égale au “travail”
de leur résultante (S Fe x t)
. A B, tous les points du solide ayant le même déplacement
A B que le centre d’inertie. Remarque: la relation D(1
/
2 . M VG 2 ) = 1 / 2 . M VB2
- 1 / 2 . M VA 2 = (S
Fe x t) . A B est valable en fait sans restriction quel que
soit le mouvement, même pour un système déformable
(elle est une conséquence du théorème du centre d’inertie).
Travail et énergie potentielle de pesanteur
Le choix fait a pour but d’éviter les changements du système
étudié lors de l’analyse énergétique de l’interaction
d’un corps avec la Terre :
le système est le solide soumis à une force extérieure
connue (à la surface de la Terre : le poids). C’est pour cela que
l’énergie potentielle d’interaction solide-Terre est désignée
dans la colonne centrale Contenus par “énergie potentielle d’un
solide en interaction avec la Terre”.
On introduit qualitativement la variation d’énergie potentielle
de pesanteur comme étant le travail qu’il faut fournir pour éloigner
un corps du centre de la Terre d’un point A à un point B, le corps
étant au repos en A et en B. Pour élever le centre d’inertie
de ce corps de l’altitude Z A à l’altitude Z B
il faut lui appliquer et faire travailler une force F (c’est la force exercée
par l’opérateur). L’application de la loi précédente
s’écrit alors :
1 / 2 . M VB 2 - 1 / 2
. M VA 2 = S WA B(Fe
x t) = WAB (P) + WAB (F) .
VA et VB étant nulles, on en déduit
que WAB (F) = - WAB (P) = Mg(Z B - Z A
) .
L’énergie potentielle de pesanteur est définie par la
grandeur Mgz , z étant l’altitude.
Pour illustrer la transformation d’énergie potentielle en énergie
cinétique, on pourra faire un retour sur la chute libre ou sur un
mouvement de projectile et constater que la somme 1 / 2 . M
VG2 + Mgz est constante. On fait remarquer la cohérence
du discours énergétique introduit dans la partie précédente,
à savoir que du travail pouvait accroître l’énergie
cinétique d’un corps. Ici il accroît son énergie potentielle,
qui elle-même peut ultérieurement se transformer en énergie
cinétique.
On aborde ainsi une première fois la conservation de l’énergie
sans pour autant l’évoquer de manière explicite aux élèves.
Autres effets du travail
L’idée directrice est qu’en plus de son énergie cinétique
et de son énergie potentielle d’interaction avec la Terre, un corps
peut aussi stocker de l’énergie qui se manifeste à l’échelle
macroscopique sous diverses formes plus ou moins indépendantes les
unes des autres (déformation élastique, variation de température
et/ou de pression, changement d’état physico-chimique...).
Par exemple le mouvement relatif de deux solides en contact, en présence
de forces de frottement, s’accompagne généralement d’une
élévation de température de chacun des solides.
Autres exemples : l’énergie stockée différemment
dans un ressort, un élastique, un gaz comprimé, un accumulateur,
qui peut , au moins en partie, être récupérée
en mettant par exemple des corps en mouvement (lanceur d’un flipper, arbalète,
carabine à ressort, moteurs à ressort, voiture électrique...)
Toutes ces formes d’énergie sont regroupées sous la dénomination
“énergie interne U”. Aucune expression de l’énergie interne
ne sera proposée.
Un autre mode de transfert d’énergie
: le transfert thermique
En apportant de l’énergie par travail mécanique ou électrique
(plus tard pour ce dernier point) on peut échauffer un corps, d’où
l’idée qu’en général à une élévation
de température correspond une énergie stockée plus
importante.
On s’appuie ensuite sur l’étude de situations simples dans lesquelles
un système voit son énergie évoluer (par exemple un
corps chaud qu’on laisse refroidir au contact de l’air atmosphérique
ou un corps froid placé au contact d’une source chaude). On définit
alors un deuxième mode de transfert d’énergie: le transfert
thermique (cette expression sera utilisée de préférence
au terme de chaleur pour éviter la confusion trop fréquente
entre chaleur et température).
On indique qu’à l’échelle macroscopique, ce transfert
d’énergie s’effectue spontanément du système dont
la température est la plus élevée vers celui dont
la température est la plus basse. On se limite dans cette première
approche au transfert thermique par conduction. Cette notion de transfert
thermique sera réinvestie dans l’enseignement de SVT.
Il a été vu en classe de seconde que la température
est la variable macroscopique rendant compte de l’agitation des molécules
d’un gaz. Le transfert thermique est un mode de transfert désordonné
qui s’interprète à l’échelle microscopique par des
transferts d’énergie lors d’interactions concernant des particules
situées à l’interface entre le système et son environnement.
Le transfert d’énergie par rayonnement ne fait ici l’objet que
d’une approche simple et qualitative à partir d’exemples courants
(soleil, lampe...)
Approche du principe de conservation de l’énergie.
On pourra conclure cette partie présentant le principe de conservation
de l’énergie sous la forme : à tout système dans un
état donné, on peut associer une grandeur appelée
“énergie”. Si l’énergie d’un système augmente ou diminue,
c’est qu’il a reçu ou cédé de l’énergie, que
ce soit sous la forme de travail, de transfert thermique ou de rayonnement.
Haut
de cette page 
Leçon 6 : Travail et puissance d'une
force constante
Sommaire : Travail personnel, travail d'une force,
travail du poids d'un corps, travail d'une force constante quel que soit
le trajet suivi par le corps, travail d'une force de frottement, puissance
d'une force.
6.0. Travail personnel
Vous avez à soulever (seul et sans l'aide d'un moteur) une
énorme pierre, pour la poser sur un mur.
Connaissez-vous des mécanismes permettant d'y parvenir ?
Aujourd'hui, vous pouvez louer pour cela un bulldozer. La force de
soulèvement exercée par le bulldozer sur la pierre est-elle
différente de celle que vous pouvez exercer à l'aide d'un
des mécanismes précédents ?
Quelle sera la vraie différence entre les deux méthodes
?
6.1. Travail d'une force
6.1.1. Paramètres dont dépend le travail
Envisagez les exemples suivants :
-
Vous poussez, sans succès, c'est à dire sans réussir
à le faire avancer, votre véhicule bloqué par un bourrelet
de neige. La valeur de la force exercée est de 200 N, la durée
de l'effort de 20 secondes.
-
Vous poussez votre véhicule. Le frein à main ayant été
légèrement serré, le véhicule ne prend quasiment
pas de vitesse, mais parcourt 5 mètres. La force exercée
vaut 200 N, la durée de l'effort est toujours de 20 s.
-
Vous procédez comme dans l'exemple 2, mais le frein étant
moins serré, une force de 100 N suffit.
-
Vous renouvelez l'exercice n° 2, avec une force de 200 N, mais déplacez
votre véhicule de 10 mètres, toujours à vitesse quasi
nulle.
-
Dans l'exercice n° 2, pendant que vous poussez, un ami essaie de soulever
le véhicule. Quel travail fournit-il ?
Comparez le travail effectué par la force appliquée au véhicule,
dans les différents cas.
Dans le premier cas, vous n'avez effectué aucun travail mécanique,
au sens du physicien. Même si vous êtes épuisé.
Il serait intéressant de savoir quelle énergie votre organisme
a dépensé en vain.
Dans le dernier cas, votre ami n'a effectué aucun travail non
plus.
Conclusion : Le travail d'une force dépend de :
-
La valeur de la force,
-
la longueur du déplacement,
-
l'angle entre les directions de la force et du déplacement.
6.1.2. Définition du travail d'une force constante
Le travail W d'une force constante 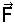 dont
le point d'application se déplace de A en B est numériquement
égal au produit scalaire du vecteur modélisant la force,
par le vecteur
dont
le point d'application se déplace de A en B est numériquement
égal au produit scalaire du vecteur modélisant la force,
par le vecteur 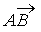 représentant
le déplacement :
représentant
le déplacement :
W = 
|
Cette expression peut aussi s'écrire W = F . AB . cosa,
où a est l'angle entre 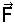 et
et 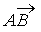 .
.
Le travail W se mesure en joule (symbole J), la valeur F de la force
en newton et le déplacement L ou AB en mètre.
// Note : Le symbole W a été choisi pour le travail,
à partir du mot anglais work. Il faut dire que le symbole T est
déjà lourdement mis à contribution (durée,
température, date, période). Ne confondez pas ce symbole
d'une grandeur physique avec le symbole de l'unité de puissance,
abordée au paragraphe 5.
6.1.3. Cas particuliers
Si la force est perpendiculaire au déplacement, son
travail est nul.
Si la force est de même direction et de même sens que le
déplacement, son travail est moteur (valeur positive) et
peut se simplifier en : W = F . L, où F est la valeur de la force
et L la longueur du déplacement.
Si la force est de même direction que le déplacement et
de sens contraire, son travail est résistant (valeur négative)
et peut se simplifier en : W = - F . L, où F est la valeur de la
force et L la longueur du déplacement.
6.1.4. Travail de plusieurs forces
Si plusieurs forces sont exercées sur un corps, et si toutes
les forces se déplacent selon le même vecteur (soit le corps
est ponctuel, soit il est animé d'un mouvement de translation),
deux méthodes sont possibles pour calculer leur travail total :
-
W =
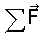 . L,
(note : L est un vecteur) ou
. L,
(note : L est un vecteur) ou
-
W = (
 ) . L,
ou encore
) . L,
ou encore
-
W = W1 + W2 + W3
Ce qui peut s'énoncer : Le travail total est égal au travail
de la somme des forces, ou bien, le travail total est égal à
la somme des travaux de chaque force.
Vérifiez que les propriétés du produit scalaire
conduisent bien au même résultat.
Notez que dans le premier cas, vous faites une somme vectorielle et
dans le deuxième une somme de nombres réels, plus facile.
6.2. Travail du poids d'un corps
Supposons qu'un corps se déplace dans une zone de dimension
raisonnable (quelques kilomètres).
Lorsque le centre de gravité du corps passe du point A d'altitude
zA au point B d'altitude zB, son poids 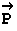 fournit
le travail :
fournit
le travail :
WA->B(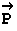 )
= m . g . ( zA - zB) )
= m . g . ( zA - zB)
|
Remarquez que ce travail ne dépend pas du trajet suivi.
6.3. Travail d'une force, constante quel que soit le trajet suivi par le
corps
Comme dans le cas précédent, ce travail ne dépend
que de la force et du vecteur déplacement de A, point initial, à
B, point final. Le trajet suivi entre A et B n'a pas d'importance.
6.4. Travail d'une force de frottement
Dans le cas où un solide glisse sur un support, il est commode
de décomposer l'action du support sur le solide en une composante
R normale au support, donc perpendiculaire au déplacement, dont
le travail est nul, et une force f de frottement, tangente au support,
dirigée vers l'arrière du mouvement, et qui fournit un travail
résistant - f L, où L est la longueur du déplacement.
6.5. Puissance d'une force
Cela nous ramène au travail
personnel du début de cette leçon.
La vraie différence entre le soulèvement d'une pierre
à l'aide d'un treuil ou d'un bulldozer n'est pas dans la valeur
de la force exercée, mais dans la rapidité de l'action. Insistons
: Le bulldozer n'est pas plus fort qu'un homme muni d'un treuil ; il est
plus rapide parce que plus puissant.
6.5.1. Définition
La puissance moyenne P d'une force est numériquement égale
au quotient du travail W fourni par cette force, par la durée T
nécessaire pour fournir ce travail.
La puissance P se mesure en watt (symbole W), W en joule et T en seconde.
6.5.2. Puissance d'une force et vitesse de déplacement de son point
d'application
Si le point d'application se déplace à la vitesse
v, pendant la durée T, il se déplace de v . T. La puissance
s'écrit donc P = F . v. Cette relation reste vraie même si
le vecteur vitesse v n'est pas constant, donc si v est le vecteur vitesse
instantanée du point d'application de la force.
6.5.3. Ordres de grandeur
Puissance
-
d'un laser du laboratoire de physique ou d'une diode laser du commerce
: 3 mW
-
d'une lampe : 60 W,
-
d'un homme dans un effort de longue haleine : 70 W,
-
d'un cheval (vapeur) : 736 W,
-
d'une plaque de cuisinière électrique, ou d'un radiateur
électrique : 1500 W,
-
d'un assez grand panneau solaire (1 mètre carré, coût
6000 F), en plein Soleil : 100 W,
-
d'une motrice de TGV : 6,4 MW
-
d'un réacteur nucléaire : 900 MW
6.5.4. Puissance de plusieurs forces
La puissance fournie par plusieurs forces est égale à
la somme des puissances fournies par chacune des forces, ou encore à
la puissance fournie par la somme (vectorielle) des forces.
Et ceci comme précédemment,
dans le cas où chaque force se déplace selon le même
vecteur.
6.6. Exercices
Page 106 et suivantes : Contrôler ses connaissances ; exercices
2, 5 (plan incliné, délicat), 7, 8, 10 (plan incliné),
14 (satellites).
6.7. Travail pratique
6.7.1. Matériel, fiche pour le préparateur
Salle informatique
Excel
Logiciel LireAvi ou équivalent
Fichiers 2balles.avi et vélo.avi
6.7.2. Fiche élève
Travail et énergie cinétique
Vous devrez comparer le travail des forces extérieures appliquées
à un solide à la variation d'énergie cinétique
du même solide, dans un référentiel galiléen.
1. Chute libre d'une balle de tennis
Ouvrez dans LireAvi le fichier 2balles.avi
Transférez les coordonnées successives du centre d'inertie
de la balle de tennis dans un tableur (éliminez la première
image).
Choisissez le référentiel.
Faites un bilan des forces appliquées à la balle. La
masse de celle-ci est de 58,1 g.
Calculez aux différentes positions successives le travail fourni
par ces forces.
Calculez l'énergie cinétique de la balle en ces différentes
positions.
Comparez.
2. Conséquences d'éventuelles erreurs
Un élève a mal lu son énoncé et a choisi
pour la balle de tennis une masse de 58,1 kg. Sa conclusion sera-t-elle
correcte malgré tout ?
Un autre a indiqué au logiciel LireAvi que la partie visible
de la règle est longue de 7 m au lieu de 70 cm. Sa conclusion sera-t-elle
correcte ?
3. Chute libre d'une balle de tennis
Ouvrez dans LireAvi le fichier vélo.avi
Transférez les coordonnées successives du centre d'inertie
de la balle de tennis dans un tableur (uniquement la première partie
du mouvement, avant que la balle ne touche le sol). Le diamètre
intérieur de la roue du VTT est de 55 cm.
Choisissez le référentiel.
Faites un bilan des forces appliquées à la balle.
Calculez aux différentes positions successives le travail fourni
par ces forces.
Calculez l'énergie cinétique de la balle en ces différentes
positions.
Comparez.
Remarque : L'énergie cinétique s'écrit
Ec = 1/2 . m . v2.
Le théorème de Pythagore permet de retrouver facilement
v2. En effet v2 = vHorizontale2
+ vVertivale2.
Or vHorizontale est constante dans ce mouvement ; elle est
égale à la vitesse du cycliste au moment où il a lâché
la balle.
Haut
de cette page 
Leçon 7 : Énergie cinétique
Sommaire : Travail personnel, vitesse d'un solide
tombant en chute libre, énergie cinétique d'un solide en
translation, théorème de l'énergie cinétique,
cas particuliers (mouvements de translation), le travail est un transfert
d'énergie.
// Nous n'envisagerons que des mouvements de translation.
7.0. Travail personnel
Vrai ou faux ?
Lorsqu'un véhicule automobile, roulant à 65 km . h-1,
heurte frontalement un obstacle indéformable, cela revient à
une chute de 17 mètres, du haut d'un immeuble de 5 étages.
La distance de freinage d'un véhicule, hors délai de réaction
du conducteur, est proportionnelle au carré de la vitesse. Si la
force de frottement (freinage) a même valeur que le poids du véhicule
(ce qui impose d'excellents pneumatiques et une route parfaitement sèche),
un véhicule lancé à 130 km . h-1 a besoin
de 67 mètres pour s'arrêter, alors qu'à 65 km . h-1
il lui suffirait de 4 fois moins, soit 17 mètres.
Lorsqu'une balle en plomb heurte un mur, elle fond.
Application : Des valeurs précédentes qui sont
toutes justes, déduisez la hauteur de l'immeuble dont devrait tomber
un véhicule automobile pour que le choc soit aussi violent que s'il
roulait à 130 km . h-1.
Réponse : 67 mètres, soit 24 étages. En ce cas,
il ne peut y avoir de survivant parmi les passagers.
7.1. Vitesse d'un solide tombant en chute libre
On dit qu'un solide tombe en chute libre, s'il n'est soumis qu'à
son poids. Les forces de frottement dans l'air doivent donc pour cela être
négligeables.
Des expériences montrent qu'au début de leur chute (s'ils
partent sans vitesse initiale) tous les solides sont en chute libre.
L'expérience montre que, si un solide tombe en chute libre, avec
une vitesse initiale nulle, la valeur v de sa vitesse est liée à
la hauteur de chute h par la relation :
avec v mesurée en mètres par seconde, g, intensité
de la pesanteur, g = 9,81 m . s-2 ou N . kg-1 et
h en mètres.
Remarquez que la masse du solide n'intervient pas dans cette relation
: Dans une chute libre, tous les solides ont le même mouvement. Nous
avons déjà dit que c'est vrai au tout début de leur
chute pour tous les solides. Ensuite, leur vitesse augmentant, les forces
de frottement deviennent plus ou moins vite non négligeables. Leur
forme et leur masse volumique va intervenir. Les corps les plus compacts
et lourds vont être pendant plus longtemps en chute libre.
Proposez une expérience permettant d'observer la chute libre
sur environ 1 mètre d'un bloc de plomb et d'une plume.
Réponse : Chute dans un tube vidé de son air, expérience
réalisée déjà par Newton.
7.2. Énergie cinétique d'un solide en translation
Lors d'une chute libre entre les points A et B, c'est le travail
du poids qui provoque l'augmentation de l'énergie cinétique.
Or :
WA->B(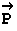 )
= m . g . h ou en tirant g . h de l'expression du paragraphe précédent
: g . h = v2 / 2
)
= m . g . h ou en tirant g . h de l'expression du paragraphe précédent
: g . h = v2 / 2
WA->B(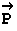 )
= 1/2 m [(vB)2 - (vA)2] et
)
= 1/2 m [(vB)2 - (vA)2] et
WA->B(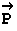 )
= m . g .(zA - zB). Donc nous pouvons donner la définition
de l'énergie cinétique (si l'identification terme à
terme ne vous convainc pas, prenez le cas particulier du solide tombant
en chute libre avec une vitesse initiale vA nulle).
)
= m . g .(zA - zB). Donc nous pouvons donner la définition
de l'énergie cinétique (si l'identification terme à
terme ne vous convainc pas, prenez le cas particulier du solide tombant
en chute libre avec une vitesse initiale vA nulle).
| Un solide de masse m, animé d'un mouvement de translation
de vitesse v, possède une énergie cinétique donnée
par la relation :
Ec = 1/2 m . v2
|
L'énergie cinétique se mesure en joule, m en kilogramme,
v en mètre par seconde.
Notez que l'énergie cinétique dépend du référentiel.
// Remarque : Nous avons trouvé l'expression
de l'énergie cinétique, à partir de résultats
expérimentaux ; en classe de terminale, vous disposerez des outils
physiques et mathématiques permettant la démonstration complète
de la relation.
7.3. Théorème de l'énergie cinétique
// Note : Apprenez ce théorème
parfaitement (par cœur) ; il vous servira souvent et vous devrez à
chaque fois rappeler son énoncé.
Il s'agit d'une généralisation du résultat précédent
: La force exercée sur le solide peut être autre que son poids
; il peut y avoir plusieurs forces.
|
Dans un référentiel galiléen, la variation
d'énergie cinétique d'un solide entre deux instants est égale
à la somme des travaux, entre ces deux instants, des forces appliquées
à ce solide.
|
Pour une force exercée :
Ec (B) - Ec (A) = WA->B (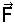 ) )
|
Pour plusieurs forces exercées :
Ec (B) - Ec (A) =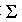 WA->B
(
WA->B
(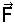 i
), ou encore :
i
), ou encore :
Ec (B) - Ec (A) = WA->B (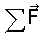 i
)
(uniquement s'il s'agit d'un mouvement de translation, car il faut que
les forces se déplacent selon le même vecteur).
i
)
(uniquement s'il s'agit d'un mouvement de translation, car il faut que
les forces se déplacent selon le même vecteur).
7.4. Cas particuliers (mouvements de translation)
7.4.1. Les forces effectuent sur le solide un travail moteur
W = > 0
> 0
Ce travail est positif, l'énergie cinétique de translation
augmente, la valeur de la vitesse du solide augmente.
7.4.2. Les forces effectuent sur le solide un travail résistant
W = < 0
< 0
Le travail est négatif, la valeur de la vitesse du solide diminue.
7.4.3. Les forces appliquées au solide effectuent un travail nul
W = = 0, donc la résultante
= 0, donc la résultante 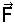 est perpendiculaire au déplacement.
est perpendiculaire au déplacement.
La valeur de la vitesse du solide reste constante.
Deux cas se présentent :
-
Si les forces se compensent, le vecteur vitesse du solide en translation
est constant ; le mouvement est rectiligne uniforme ; ceci est conforme
au principe de l'inertie.
-
Sinon, le vecteur somme des forces est perpendiculaire au déplacement
; la valeur de la vitesse est constante, mais le vecteur vitesse change
de direction.
7.5. Le travail est un transfert d'énergie
Lorsque un joueur lance un ballon, le travail moteur de la force
qu'il exerce sur la ballon augmente l'énergie cinétique de
celui-ci. Le travail de cette force a transféré de l'énergie
du joueur au ballon.
7.6. Exercices
Page 120 et suivantes, exercices 8, 13 (crash-test), 14, 16 (pendule,
difficile).
7.7. Travail pratique
7.7.1. Matériel, fiche pour le préparateur
Salle informatique
Excel
Logiciel LireAvi ou équivalent
Fichiers 2balles.avi et vélo.avi
7.7.2. Fiche élève
Énergies
Vous devrez comparer les différentes énergies, cinétique
et potentielle de pesanteur, de solides en chute libre ou non, dans un
référentiel galiléen.
1. Chute libre d'une balle de tennis
Ouvrez dans LireAvi le fichier 2balles.avi
Transférez les coordonnées successives du centre d'inertie
de la balle de tennis dans un tableur (éliminez la première
image).
Choisissez le référentiel.
Faites un bilan des forces appliquées à la balle. La
masse de celle-ci, directement donnée par une balance électronique,
est de 58,1 g (masse de l'air déplacé : 0,17 g)
Calculez aux différentes positions successives l'énergie
cinétique de la balle et son énergie potentielle de pesanteur.
Comparez ces énergies. Pour cela, il pourra être astucieux
d'en faire la somme.
2. Chute freinée d'une boule de polystyrène
Transférez les coordonnées successives du centre d'inertie
de la boule de polystyrène dans un tableur (éliminez la première
image).
Choisissez le référentiel.
Faites un bilan des forces appliquées à la balle. La
masse de celle-ci est de 5,59 g (masse de l'air déplacé :
0,22 g).
Calculez aux différentes positions successives l'énergie
cinétique de la balle et son énergie potentielle de pesanteur.
Comparez ces énergies.
Haut
de cette page 
Leçon 8 : Énergie potentielle
Sommaire : Travail personnel, énergie potentielle
gravitationnelle ou de pesanteur, énergie mécanique.
8.0. Travail personnel
Vous êtes le (riche) propriétaire d'un parc impressionnant
d'éoliennes produisant de l'énergie électrique. Mais
voilà, les éoliennes ne tournent que quand il y a du vent,
et il n'y a pas forcément de vent lorsque vous avez besoin d'électricité.
Proposez différentes façons de stocker cette énergie
pour qu'elle soit disponible au bon moment.
Quelques unes des réponses possibles
Si la puissance fournie est très faible, l'énergie
pourra être stockée dans des batteries d'accumulateurs. Problème
: les accumulateurs sont très coûteux, donc correspondent
à un important dégagement de gaz à effet de serre
lors de leur fabrication, et de plus le plomb ou le nickel qui les constituent
sont très polluants.
Dans le cas contraire, une solution est de pomper de l'eau et de remplir
un bassin situé en altitude, puis de récupérer l'énergie
potentielle de pesanteur ainsi stockée, au moment opportun,
en faisant tourner des turbines. Problème : Le coût de cette
solution (production de gaz à effet de serre lors de la fabrication
du ciment, des terrassements... ), l'impact sur le paysage, l'opposition
d'associations.
Boutade : Le plus simple est de vendre cette électricité
au prix fort à EDF qui se débrouillera avec. Vous ferez une
bonne affaire et en plus, vous aurez bonne conscience. Ce n'est pas simplement
une boutade, puisque c'est devenu depuis peu une réalité.
8.1. Énergie potentielle gravitationnelle, ou de pesanteur
8.1.1. Exemples
L'eau accumulée derrière un barrage d'altitude peut
faire tourner des turbines ; un poids d'horloge en descendant lentement
fournit au balancier l'énergie que celui-ci a perdu à cause
des frottements ; un mouton, lourde pièce métallique, est
soulevé par l'explosion d'un mélange air-essence, puis il
retombe et enfonce un pieu en béton dans le sol. Dans tous ces cas,
il est possible de dire que de l'énergie due à la pesanteur
a été accumulée.
Notez que dans le dernier exemple, cette énergie devient d'abord
énergie cinétique du mouton, avant de vaincre les forces
de frottement du pieu dans le sol.
Un corps situé en altitude possède de l'énergie
en réserve, appelée énergie potentielle gravitationnelle.
Un ressort, un arc, tendus, possèdent aussi de l'énergie
en réserve, appelée énergie potentielle élastique.
8.1.2. Expression de l'énergie potentielle de pesanteur
Imaginons un solide de masse m dont le centre de gravité
G est soulevé très lentement d'une hauteur h. Si le référentiel
terrestre est doté d'un axe vertical, orienté vers le haut,
permettant de repérer les altitudes z (ou cotes) de G, si le point
de départ est A et le point d'arrivée B, la hauteur h s'écrit
: h = zA - zB.
Pour soulever le solide dans ces conditions, il suffit de lui appliquer
une force directement opposée à son poids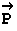 .
Le travail fourni au solide par la force est donc l'opposé du travail
fourni par
.
Le travail fourni au solide par la force est donc l'opposé du travail
fourni par 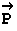 ,
soit m . g (zB - zA). Ce travail est l'énergie
potentielle de pesanteur accumulée. En choisissant une origine,
à notre convenance, pour l'axe des z, mais en n'oubliant pas de
préciser quel est notre choix, et en décidant qu'à
l'altitude ou cote z = 0, l'énergie potentielle de pesanteur du
solide est nulle, la relation précédente devient :
,
soit m . g (zB - zA). Ce travail est l'énergie
potentielle de pesanteur accumulée. En choisissant une origine,
à notre convenance, pour l'axe des z, mais en n'oubliant pas de
préciser quel est notre choix, et en décidant qu'à
l'altitude ou cote z = 0, l'énergie potentielle de pesanteur du
solide est nulle, la relation précédente devient :
Avec EP, énergie potentielle de pesanteur exprimée
en joule, m, masse du solide en kilogramme, g intensité de la pesanteur
en N . kg-1 (g = 9,81 kg-1) et z, altitude du centre
de gravité en mètre, donc avec un axe des cotes orienté
vers le haut.
// Note : L'origine des cotes z peut être choisie où
vous le souhaitez, donc, de préférence, de manière
à simplifier les calculs. Mais il ne faut jamais oublier de dire
quel a été votre choix.
Comment retrouver cette relation, sans erreur sur les signes
?
Si vous n'y prenez garde, vous risquez de confondre l'expression précédente
de l'énergie potentielle de pesanteur, avec celle donnant le travail
du poids ; par ailleurs, dans certains problèmes, les axes verticaux
sont orientés vers le bas, donc z devient - z. Pour éviter
les erreurs, une méthode consiste à imaginer un solide qui
prend de l'altitude. S'il part de z = 0, z devient positif pour un axe
orienté vers le haut, négatif dans le cas contraire. Dans
les deux cas, son énergie potentielle de pesanteur augmente et passe
de 0 à une valeur positive. Le travail du poids est négatif
par contre. Donc écrivez l'expression puis attribuez-lui le signe
convenable.
8.2. Énergie mécanique
Revenons sur l'étude du mouvement du centre de gravité
d'un solide en chute libre. Nous avons trouvé expérimentalement
la loi donnant la vitesse instantanée v atteinte par son centre
de gravité, en fonction de la hauteur de chute: v2 =
2 . g . h. ceci nous a permis de trouver la définition de l'énergie
cinétique de translation.
Imaginons maintenant que nous ayons démontré (ce sera
fait en classe de terminale) l'expression de l'énergie cinétique.
Appliquons nos nouvelles connaissances à l'étude de ce problème
: Au point de départ, le solide a une énergie cinétique
Ec nulle, il a une énergie potentielle de pesanteur EP
de valeur m . g . h et éventuellement une énergie K sous
d'autres formes inconnues. A l'arrivée, son énergie potentielle
de pesanteur est nulle, son énergie cinétique Ec
vaut 1/2 m . v2 et K est toujours inconnue, mais n'a pas changé
(le solide ne s'est pas déformé, échauffé...
). Si ce dernier point vous pose problème, imaginez l'état
du solide, une fraction de seconde avant qu'il touche le sol, à
l'altitude 0.
Comme la chute a été libre, il n'y a pas eu de perte d'énergie
par frottement. Nous pouvons donc écrire :
Énergie initiale = énergie finale, ou
ECi + EPi + K = ECf + EPf
+ K, ou encore,
0 + m g h = 1 / 2 m v2, ou finalement :
v2 = 2 . g . h.
Si le solide glisse sans frottement ( pas de perte d'énergie)
sur une piste de forme quelconque et s'il n'y a pas de frottements dans
l'air, la méthode reste valable. S'il y a frottement, tout se complique,
mais des hypothèses simplificatrices permettent peut-être
de calculer grossièrement les pertes d'énergie, et d'appliquer
encore cette méthode qui est donc extrêmement puissante.
Notez bien que dans cette méthode, le poids du solide n'est pas
évoqué car son travail est déjà compris dans
l'opposé de la variation d'énergie potentielle de pesanteur.
Ne le comptez pas 2 fois !
La somme EC + EP est appelée énergie
mécanique Em. Elle joue un rôle important en mécanique,
car elle permet de résoudre des problèmes de façon
efficace. C'est une intégrale première du mouvement.
8.3. Exercices
Exercice 1
Votre consommation familiale d'énergie électrique
est de 45 millions de joules chaque jour (12,6 kW h). Vous produisez cette
énergie à l'aide d'une éolienne et souhaitez stocker
une semaine d'énergie, par mesure de précaution.
Vous décidez de réaliser un bassin rempli d'eau. Ce bassin
a une surface au sol carrée et une profondeur constante de 5 mètres
(pour simplifier les calculs). Lorsque l'eau restitue son énergie
potentielle de pesanteur, elle descend de 10 mètres. Quelle doit
être la dimension d'un côté du bassin ?
Réponse : La masse m d'eau est telle que
m . g . h = 7 x 45000000 J.
Avec g = 10 N/kg et h = 10 m, la masse d'eau est m = 3150000
kg. Le volume d'eau est de 3150 m3. Le bassin a un côté de
25 m.
Ces calculs supposent qu'il n'y a pas de perte d'énergie.
Vraisemblablement, le bassin devra être 2 fois plus grand.
Exercices du livre :
Page 134 et suivantes, exercices 7, 8, 9, 16.
Haut de
cette page 
Leçon 9 : Transferts d'énergie
Sommaire : Énergie interne, travail d'une
force, transfert thermique, transfert d'énergie par rayonnement,
l'énergie d'un système.
9.1. Énergie interne
Tout système possède une énergie microscopique,
appelée énergie interne U, somme
-
de l'énergie cinétique microscopique d'agitation désordonnée
des particules constituant le système,
-
de l'énergie potentielle d'interaction de ces particules et
-
d'autres formes d'énergie, chimique, nucléaire...
Cette énergie interne peut être modifiée de diverses
manières.
9.2. Travail d'une force
Le travail d'une force peut modifier l'énergie cinétique
macroscopique d'un système (exemple : une fusée accélère
sous l'effet de la poussée des réacteurs, elle gagne de l'énergie
cinétique) ; il peut modifier l'énergie potentielle macroscopique
d'un système (exemple : Une cage d'ascenseur s'élève
sous l'effet de la traction d'un câble; elle gagne de l'énergie
potentielle de pesanteur).
Mais le travail d'une force peut avoir des effets au niveau microscopique,
donc de l'énergie interne d'un système :
-
Il peut déformer un corps. Exemple, un ressort de suspension qui
se comprime. Il ne faudra pas compter 2 fois cette énergie (énergie
potentielle élastique OU énergie d'interaction microscopique),
-
il peut échauffer un corps. Exemples, disques de freins, allumage
d'un feu en frottant deux solides,
-
il peut faire changer d'état un corps. Exemple, fusion d'une balle
en plomb lorsqu'elle heurte un obstacle.
9.3. Transfert thermique
9.3.1. Définition
Il y a transfert thermique, lorsque deux corps de températures
différentes sont en contact.
9.3.2. Propriété
Un transfert thermique Q s'effectue toujours du corps chaud vers
le corps froid.
9.3.3. Conduction
Exemple : Vous chauffez de l'eau dans une casserole métallique,
sur une plaque électrique. De l'énergie est transférée
à l'eau, dont l'énergie interne augmente. Il n'y a pas de
déplacement de matière.
Ne confondez pas : La plaque électrique fournit de l'énergie
à la casserole ; on dit aussi qu'elle lui fournit de la chaleur.
L'agitation des molécules d'eau augmente, donc la température
de l'eau augmente.
La conduction est un mode de transfert thermique qui s'effectue sans
transport de matière.
Exemples : Est-il plus agréable de remuer son café
brûlant avec une petite cuillère en acier inoxydable, ou avec
une cuillère en argent ?
Un acteur célèbre a (paraît-il) fait installer
chez lui des lunettes de WC en or massif. Expliquez pourquoi vous ne souhaitez
pas qu'il vous invite.
Trêve de plaisanterie. On se brûle effectivement avec une
petite cuillère en argent.
9.3.4. Convection
Dans un système de chauffage central, l'eau chaude ayant
tendance à monter, l'eau froide à descendre, la seule mise
en marche de la chaudière suffit à chauffer un appartement
ou une maison, par convection naturelle. Souvent, un circulateur (pompe)
accélère la circulation naturelle de l'eau.
La convection est un mode de transfert thermique qui s'effectue avec
transport de matière.
9.3.5. Transfert thermique par rayonnement
Le transfert d'énergie par ondes électromagnétiques
est appelé rayonnement.
Tout corps émet un tel rayonnement.
Un être vivant à corps chaud émet un rayonnement
infra rouge, détectable par certains serpents et les caméras
infra rouge.
Un morceau de métal à haute température émet
un rayonnement visible, rouge ou même blanc.
Un métal à très haute température (filament
de tungstène d'une lampe quartz halogène) émet un
rayonnement visible blanc et de l'ultra violet. Il faut filtrer ce rayonnement
pour qu'il ne soit pas nocif.
9.3.6. Calcul d'un transfert thermique
Un transfert thermique peut provoquer une variation de température,
ou un changement d'état.
Dans le premier cas, Q = m . c .(qf
-
qi),
où Q est le transfert thermique en joule, m, la masse du corps en
kilogramme, c, la capacité thermique massique du corps en J.kg-1.°C-1
et
qf et qi
les températures finale et initiale du corps.
Pour l'eau, c = 4180 J.kg-1.°C-1 ,
pour le fer c = 450 J.kg-1.°C-1 .
Dans le deuxième cas, Q = m . L, avec L chaleur latente
massique de changement d'état, en J.kg-1 .
Pour l'eau solide -> liquide, à 0 °C, L = 335 . 103
J.kg-1. Pour l'eau liquide -> vapeur, à 100 °C, sous
une pression de 1 bar, L = 2261 . 103 J.kg-1. Pour
le fer solide -> liquide, à 1535 °C, L = 270 . 103
J.kg-1.
9.4. L'énergie d'un système
On appelle système isolé, un système qui n'échange
pas d'énergie avec l'extérieur.
L'énergie d'un système isolé est constante.
Les physiciens admettent le principe de conservation de l'énergie.
9.5. Exercices
Page 148 et suivantes, exercices 4 (très complet), 6 (bouteille
thermos - ajouter : un radiateur chromé est-il un bon radiateur
?), 12, 14 (capacité thermique d'un calorimètre).
9.6. Travail pratique, capacité thermique d'un calorimètre
9.6.1. Matériel, fiche pour le préparateur
Au bureau :
Bouilloire (sinon, plaques chauffantes),
réserve d'eau distillée.
Pour 9 groupes d'élèves :
1 calorimètre,
1 thermomètre,
1 balance électronique,
2 béchers de 150 mL
// Note : Les thermomètres à thermocouples sont très
satisfaisants pour ce travail pratique, car ils réagissent très
vite et permettent de limiter de ce fait les pertes thermiques. La précision
obtenue est excellente.
9.6.2. Fiche élève
Travail pratique : Mesure de la capacité thermique d'un calorimètre
1. Mesure de la capacité thermique K
Introduisez 150 mL d'eau froide dans le calorimètre. Il n'est
pas nécessaire de mettre exactement 150 mL, mais vous devez mesurer
avec précision la quantité réellement mise. A l'équilibre
thermique, mesurez la température de l'eau.
Ajoutez maintenant 200 mL d'eau chaude dont vous aurez mesuré
la température.
Agitez, mesurez rapidement la température du mélange.
Calculez la quantité de chaleur Q1 reçue par
l'eau froide.
Calculez la quantité de chaleur Q2 cédée
par l'eau chaude.
Calculez la quantité de chaleur Q'1 reçue
par le calorimètre et ses accessoires.
Q'1 est proportionnelle à l'augmentation de température
du calorimètre, Q'1 = K (qFinale
- qInitiale). K est la capacité
thermique du calorimètre. Calculez K.
2. Utilisation de la valeur mesurée de K pour prédire la
température d'un mélange
Recommencez l'expérience, avec 200 mL d'eau froide et 150
mL d'eau chaude. En employant la valeur de K trouvée précédemment,
calculez la température finale qui devrait être atteinte et
comparez-la à la température finale effectivement mesurée.
9.7. Travail pratique, conversion de travail mécanique en chaleur
9.7.1. Matériel, fiche pour le préparateur
Note pour le professeur :
Les vieux appareils de Joule sont livrés avec des thermomètres
à mercure. Vous devez les remplacer par des thermomètres
à alcool, ou, plus précis, par un thermomètre à
sonde à thermocouple. Dans ce dernier cas, fabriquez une rondelle
en caoutchouc pour boucher le trou réservé au thermomètre.
Le professeur plongera dans l'eau la sonde à thermocouple, au début,
puis à la fin de l'expérience. Nous avons constaté
que, bien que plein, le cylindre ne se vide pas lorsqu'on enlève
le bouchon pour effectuer la mesure.
Au bureau :
Réserve d'eau distillée.
Un thermomètre à thermocouple.
Pour 9 groupes d'élèves :
Appareil de Joule,
accessoires et fixation de l'appareil,
masse de 5 kg,
pied à coulisse,
balance au 1/10 g,
thermomètre à alcool, si pas de thermomètre à
thermocouple.
9.7.2. Fiche élève
Travail pratique : Conversion de travail mécanique en chaleur
Attention : En aucun cas, ne mettez
un pied sous la masse de 5 kg qui peut se décrocher. Éventuellement,
placez au-dessous de cette masse votre sac de classe (sans votre calculatrice).
1. Travail de réflexion
Par frottement de la tresse en cuivre sur le cylindre en cuivre,
vous allez convertir du travail mécanique en chaleur. Comment calculer
la valeur du travail, comment mesurer la quantité de chaleur ? Quelles
sont les grandeurs que vous devrez mesurer ?
2. Mesure
Mesurez la masse du cylindre, remplissez-le d'eau et mesurez la masse d'eau
introduite.
Enroulez la tresse autour du cylindre, accrochez la masse de 5 kg,
faites vérifier le montage par le professeur.
Mesurez la température initiale.
Effectuez 750 tours de manivelle et mesurez la température finale.
3. Calculs
Calculez le travail de la force de frottement.
Calculez la quantité de chaleur reçue.
Comparez ces deux valeurs.
Données : La capacité calorifique molaire du cuivre est
de 24,5 J . mol-1 ; la masse molaire du cuivre est de 63,2 g
. mol-1.
Presque tous les solides ont une capacité calorifique molaire
égale à 3 R, R étant la constante des gaz parfaits,
figurant dans la relation PV = nRT.
4. Résultats, discussion
La masse du cylindre est de 138,6 g, la masse de la partie de la
tresse frottant sur le cylindre est d'environ 25 g, la masse d'eau introduite
est de 80,2 g. La température initiale est de 19,3 °C, la température
finale de 29,6 °C. Le diamètre extérieur du cylindre
en cuivre est de 4,78 cm. La masse suspendue à la tresse mesure
5 kg. Nous avons effectué 500 tours.
La valeur de la force de frottement est égale au poids de la
masse de 5 kg. Soit 5 x 9,81 = 49,05 N. La distance parcourue par le point
d'application de cette force est de 500 x 2 p
0,0478 / 2 = 75,08 m. Le travail mécanique fourni par la force de
frottement est de 49,05 x 75,08 = W = 3 683 J.
L'énergie transférée sert à échauffer
une partie de la tresse, le cylindre (en entier ?) et l'eau.
La quantité de chaleur reçue est :
(80,2 x 4,18 + (138,6 + 25) x 24,5/63,5)(29,6 - 19,3) = (335,2 + 63,1)
x 10,3 = Q = 4 102 J.
L'écart relatif est de (4102 - 3683) / 3683 = 11 %.
Nous avons négligé les pertes thermiques, mais avons
supposé que toute la masse du cylindre s'échauffait. Il suffit
de poser la main sur le montage, à la fin de l'expérience,
pour constater qu'il n'en est rien. Si on effectue 1000 tours de manivelle,
les pertes thermiques l'emportent, Q < W. D'où la proposition
d'effectuer 750 tours de manivelle, ce qui est une petite tricherie. Mieux
vaudrait augmenter la force de frottement, augmenter la masse d'eau, en
employant une masse de cuivre minimale. Il faudrait donc augmenter le diamètre
du cylindre en cuivre. On pourrait aussi commencer avec de l'eau à
5°C au-dessous de la température ambiante.
Haut de
cette page 
Programme officiel
III - Électrodynamique
(durée indicative 15 heures, 5 TP)
Objectifs
Dans une première partie, on montre comment se transforme
l’énergie dans un circuit électrique en soulignant l’importance
de l’effet Joule, autant dans ses applications que dans ses inconvénients.
A cette occasion l’élève va réinvestir les connaissances
sur l’introduction à l’énergie.
L’approche énergétique est privilégiée,
mais c’est aussi l’occasion de s’approprier certaines lois de l’électrocinétique.
La seconde partie comporte l’étude des forces magnétiques
sur les courants dont le rôle pratique est considérable; pour
la première fois, une action à distance est décrite
localement à l’aide d’un intermédiaire, un champ vectoriel:
le champ magnétique; les caractéristiques de la force de
Laplace sont précisées et l’utilisation de ces forces à
la conversion d’énergie électrique en énergie mécanique
permet d’enrichir les bilans abordés en mécanique.
A - CIRCUIT ÉLECTRIQUE EN COURANT CONTINU
| EXEMPLES D’ACTIVITÉS |
C O N T E N U S |
CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES |
Interpréter en termes de transferts
d’énergie qu’une lampe brille, qu’une résistance s’échauffe,
qu’un moteur tourne.
Mesures de tensions et d’intensités dans un circuit série
dans le but de calculer des grandeurs énergétiques.
Mesure du potentiel électrique de différents points
d’un circuit par rapport à celui d’un point choisi comme référence
;
tracé d’un diagramme des potentiels le long d’un circuit.
Inventorier quelques manifestations de l’effet Joule dans la vie courante.
Analyser l’influence de l’agencement des composants sur l’énergie
transférée par le générateur au reste du circuit.
Justification de l’utilisation de hautes tensions pour le transport
de l’énergie électrique.
|
1 - Transferts d’énergie au niveau d’un générateur
et d’un récepteur.
1 . 1 Énergie électrique We reçue par
un récepteur, traversé par le courant d’intensité
I, pendant Dt :
We = (VA- VB) I Dt
avec UA B= (VA- VB) >0
Puissance électrique du transfert : P = UAB
.I .
1 . 2 Effet Joule : applications
1 . 3 Énergie électrique transférée du
générateur au reste du circuit pendant la
durée D t : We = (VP-
VN) I Dt
( VP- VN) = UP N désigne la
différence de potentiel ou tension entre les bornes positive et
négative du générateur et I l’intensité du
courant qui le traverse.
Puissance électrique du transfert : P=UP N I
1 . 4 Bilan du transfert d’énergie pendant la durée D
t
Un récepteur absorbe une énergie électrique
UA B.I. Dt , en “dissipe” une partie
r.I2. Dt et convertit le reste sous
une autre forme (mécanique, chimique).
Un générateur transforme partiellement une forme d’énergie
(mécanique, chimique) E.I.Dt en énergie
électrique disponible UP N. I .Dt.
Le complément r.I2.Dt
est “dissipé” sous forme thermique par effet Joule.
2. Comportement global d’un circuit
2 . 1 Distribution de l’énergie électrique :
pendant la durée Dt :
We (générateur) = S We(récepteur)
Justification énergétique des lois d’additivité
des tensions et des intensités (loi des nœuds).
2 . 2 Étude des paramètres influant sur l’énergie
transférée par le générateur au reste d’un
circuit résistif :
- Influence de la force électromotrice E
- Influence des résistances et de leurs associations
- Relation I = E / Req
- Puissance maximale disponible aux bornes d’un générateur,
tolérée par un récepteur. |
Utiliser le principe de conservation de l’énergie pour faire
un bilan qualitatif au niveau d’un récepteur.
Mesurer une différence de potentiel.
Mesurer l’intensité d’un courant.
Réaliser un circuit d'après un schéma conventionnel
et dessiner le schéma d’un circuit réalisé.
Savoir que l’effet Joule est un effet thermique associé
au passage du courant dans un conducteur.
Représenter sur un schéma une tension par une flèche.
Savoir que, dans un circuit où il n’y a qu’un générateur,
le potentiel électrique est une grandeur qui décroît
de la borne positive vers la borne négative.
Savoir que la grandeur “puissance électrique” permet d’évaluer
la rapidité d’un transfert d’énergie.
Utiliser l’additivité des résistances en série
et des conductances en parallèle.
Faire des prévisions quantitatives lors de la réalisation
ou de la modification du circuit à partir de la relation I = E /
Req.
|
Commentaires
Lors de l’étude des transferts d’énergie concernant
un récepteur en régime permanent, l’approche du principe
de conservation de l’énergie vue à la fin de la mécanique
va permettre d’introduire simplement le fait que de l’énergie a
nécessairement été transférée du générateur
au récepteur. On utilise alors l’expression “d’énergie électrique
transférée”, notée We, de préférence
à l’expression de “travail électrique” d’usage moins courant.
Pour les bilans, on utilise les conventions “récepteur” d’une
part et “générateur” d’autre part. Les tensions sont automatiquement
algébrisées car elles se présentent comme des différences
de potentiel ; comme seuls des circuits simples, parcourus par des courants
continus, sont ici...
Accès à la partie
B.
Haut
de cette page 
Leçon 10 : Transferts d'énergie
dans un circuit électrique, générateurs et récepteurs
10.1. Énergie électrique reçue par un récepteur
Réalisons un circuit électrique comportant un générateur
et en série, une cuve à électrolyse, un moteur et
une lampe à incandescence.
Lorsque le circuit est fermé, l'énergie produite par
le générateur, énergie électrique transférée,
est convertie en
-
énergie chimique,
-
travail mécanique,
-
chaleur dans le filament de la lampe.
La puissance électrique reçue par un dipôle récepteur
de bornes A et B, traversé par un courant d'intensité I,
circulant de A vers B, à l'intérieur du récepteur,
est :
Si le dipôle est un récepteur, P, UAB (et I) sont
des grandeurs positives, P est la puissance transférée au
récepteur.
Cette relation devient :
Où W ou We est l'énergie électrique transférée,
reçue si le dipôle est un récepteur, pendant la durée
Dt.
P se mesure en watt (W), U en volt (V), I en ampère (A), t en
seconde et W en joule (J). Une énergie se mesure aussi en kilowattheure,
énergie fournie par un générateur de 1000 W, fonctionnant
pendant 1 heure. 1 kWh = 3 600 000 J.
10.2. Effet Joule
Lorsqu'un courant circule dans un circuit, du fait de la résistance
de celui-ci, l'énergie électrique transférée
est partiellement ou totalement transformée en chaleur. C'est l'effet
Joule (Angleterre, 1860). Cet effet est utilisé par les appareils
électriques chauffants et dans les lampes à incandescence.
Dans les autres cas, il conduit à des pertes d'énergie et
à des échauffements indésirables du matériel
électrique.
De la loi d'Ohm pour un conducteur ohmique, U = R . I, et de la relation
P = U . I, nous déduisons pour la puissance reçue les lois
P = R . I2 ou P = U2 / R. Cette puissance
est appelée puissance Joule. U en volt, R en ohm (W),
I en ampère, P en watt.
10.3. Quelques récepteurs, modélisation
10.3.1. Conducteur ohmique ou résistance
// Le mot résistor vient de l'Anglais.
L'intensité qui traverse un tel dipôle est proportionnelle
à la tension entre ses bornes, c'est la loi d'Ohm.
// Naturellement, la proportionnalité a des limites. La température
du conducteur ohmique ne doit pas s'élever.
10.3.2. Électrolyseur
La tension U entre les bornes d'un électrolyseur est donnée
(approximativement) par la relation
U = E' + r . I, où E' est la force contre-électromotrice
et r la résistance interne.
La puissance reçue par l'électrolyseur traversé
par l'intensité I est donnée par P = E' . I + r . I2.
Le premier terme est la puissance transférée convertie
en puissance chimique, le deuxième correspond à la puissance
transférée transformée en chaleur par effet Joule.
P en watt, U et E' en volt, r en ohm, I en ampère.
10.4. Énergie électrique fournie par un générateur
La puissance électrique fournie par un dipôle générateur
de bornes P et N, traversé par un courant d'intensité I,
circulant de P vers N, à l'extérieur du générateur
est :
10.5. Quelques générateurs, modélisation
10.5.1. Source idéale de tension
La tension délivrée ne dépend pas de l'intensité
débitée (dans des limites techniques). UPN = E.
Exemple : Alimentations Jeulin -15V, +15V. Sorties de puissance d'un
amplificateur haute fidélité (mais ici en tension alternative).
10.5.2. Pile et batterie d'accumulateurs
UPN = E - r . I
E est la force électromotrice en volt, r est la résistance
interne en ohm.
r vaut environ 1 W pour une pile et 0,01
W
pour un accumulateur au plomb.
Schéma équivalent : générateur idéal
de tension en série avec un conducteur ohmique.
10.6. Exercices
Pages 168 et suivantes, exercices 4 (différents dipôles
et convention d'orientation), 5 (pile), 9 (intensité et nombre d'électrons),
11 (puissance admissible par un conducteur ohmique), 13 (électrolyse
de l'aluminium), 18 (facultatif, décharge d'une batterie d'automobile,
quand les phares restent allumés).
10.7. Travail pratique
10.7.1. Matériel, fiche pour le préparateur
Au bureau :
3 litres de solution d'acide sulfurique de concentration environ 0,1
mol . L-1.
Pour 9 groupes d'élèves :
1 cuve à électrolyse, avec des électrodes en graphite,
éprouvette graduée de 25 mL, en verre,
1 pied, 1 noix et 1 pince pour tenir l'éprouvette,
fils,
1 voltmètre, 1 ampèremètre,
1 chronomètre,
Générateur à tension variable, descendant à
0 V, petit ELC jaune,
gants, lunettes de sécurité.
10.7.2. Fiche élève
Travail pratique : Étude d'un électrolyseur
Nous nous proposons d'étudier la caractéristique intensité
- tension et d'effectuer un bilan énergétique, pour un électrolyseur.
Celui-ci contient une solution d'acide sulfurique dans l'eau, mais la transformation
chimique observée consiste uniquement en une décomposition
de l'eau, l'acide sulfurique apportant les porteurs de charge nécessaires
au passage du courant. Quelles règles de sécurité
êtes-vous tenus de suivre ?
1. Caractéristique intensité - tension
Réalisez le montage. Appelez le professeur pour vérification.
Tracez la courbe intensité-tension de l'électrolyseur.
Prenez garde à ne pas détruire l'ampèremètre.
Au dessous de quelle valeur de tension l'électrolyse n'a-t-elle
pas lieu ? Comment s'appelle cette valeur ?
2. Bilan énergétique
Alimentez l'électrolyseur sous une tension de 3 V.
A l'instant 0, placez l'éprouvette graduée au-dessus
de l'électrode où se produit le dégagement gazeux
le plus important. Si vous ne pouvez déterminer visuellement de
quelle électrode il s'agit, cherchez à partir des données
de l'énoncé et de vos connaissances, le signe de cette électrode.
L'éprouvette doit-elle initialement être remplie d'eau
ou de solution acide ? Pourquoi ?
Mesurez l'intensité traversant le circuit.
Notez le temps t nécessaire pour
recueillir 10 cm3 de dioxygène.
Calculez l'énergie électrique transférée
au récepteur, pendant la durée t.
A partir de la courbe intensité-tension de l'électrolyseur,
calculez l'énergie électrique transférée au
récepteur, convertie en énergie chimique.
Calculez la quantité d'eau transformée en dioxygène
et dihydrogène pendant la durée t.
La transformation d'une mole d'eau correspond à une énergie
chimique de 2,8 . 105 J.
Comparez ces valeurs.
Quelle est l'énergie perdue par effet Joule ? E' et r de l'électrolyseur
mesurées au paragraphe 1 sont-elles modifiées par l'installation
de l'éprouvette ? Et si oui, dans quel sens ?
Haut de
cette page 
Leçon 11 : Circuit électrique
11.1. Énergie électrique transférée dans un
circuit
Les transferts dépendent du type de montage, série
ou parallèle.
La loi d'additivité des tensions pour un circuit série
peut s'écrire : UAB + UBC = UAC.
Qui donne UAB + UBC + UCA = UAA
= 0.
La conservation de la charge électrique conduit à la
loi des nœuds : S
IArrivant =
S
IPartant.
La somme des intensités qui arrivent à un nœud est égale
à la somme des intensités qui en repartent.
11.2. Étude prévisionnelle d'un circuit électrique
11.2.1. Association en série de conducteurs ohmiques
L'association en série de plusieurs conducteurs ohmiques
de résistances Ri est équivalente à un
conducteur ohmique de résistance Re = S
Ri . R se mesure en ohm, W.
11.2.2. Association en dérivation de conducteurs ohmiques
L'association en parallèle de plusieurs conducteurs ohmiques
de conductances Gi est équivalente à un conducteur
ohmique de conductance Ge = S Gi
.
G se mesure en siemens, S.
11.2.3. Intensité du courant électrique dans un circuit série
I = (E - E') / S Ri
11.3. Limites techniques de fonctionnement
Un générateur ne peut fournir une puissance supérieure
à un certain maximum. Parfois, il est possible de dépasser
certaines limites, mais pendant un temps très court.
De même un conducteur ohmique s'échauffe en fonctionnement.
Les conducteurs ohmiques sont vendus dans le commerce avec une indication
de leur puissance admissible.
Un échauffement exagéré peut provoquer la panne
d'un circuit électronique.
11.4. Exercices
Pages 181 et suivantes, exercices 8 (association de résistances),
9, 13 (sécurité avec les batteries d'accumulateur), 15 (bilan
de puissances), 16 (limites d'un montage).
11.5. Travail pratique
11.5.1. Matériel, fiche pour le préparateur
Au bureau :
Tiroirs de résistances diverses.
Pour 9 groupes d'élèves :
Diodes électroluminescentes rouges et vertes.
Boîte de résistances, type A.O.I.P.
Plaque à bornes.
Fils de couleur.
2 multimètres.
Alimentation Jeulin -15V, +15V.
1 oscilloscope numérique.
1 générateur basse fréquence.
3 prises BNC.
11.5.2. Fiche élève
// Réponse à la question 1 : R, 2R, 3R, 4R,
R/2, R/3, R/4, 3R/2, 5R/2, 4R/3, 5R/3, 3R/4, 3R/5, R (mais avec une puissance
admissible 4 fois plus importante, exemple de branchement d'un haut-parleur
de messages vocaux trop bruyant).
Réponse à la question 2 : En série, une résistance
suffit ; en parallèle, il faut protéger chaque DEL indépendamment.
Travail pratique : Circuits électriques
1. Associations de conducteurs ohmiques
Vous disposez de quatre conducteurs ohmiques identiques, de résistance
R. Proposez toutes les associations possibles, en calculant la résistance
équivalente obtenue. Effectuez les montages, vérifiez à
l'ohmmètre. Indiquez les montages qui vous paraissent intéressants
et dites pourquoi.
2. Diodes électroluminescentes
Tracez les caractéristiques intensité-tension d'une
diode verte et d'une diode rouge. Ne dépassez pas une intensité
de 10 mA.
Vous disposez d'une alimentation stabilisée délivrant
une tension de +5V. Branchez ces 2 diodes en série de manière
à respecter l'intensité maximale admissible, 10 mA. Notez
vos calculs et faites vérifier le montage par le professeur.
Branchez ces 2 diodes en parallèle de manière à
respecter l'intensité maximale admissible, 10 mA. Notez vos calculs
et faites vérifier le montage par le professeur.
3. Utilisation d'un oscilloscope numérique
Réalisez un montage série comportant une diode électroluminescente
et un conducteur ohmique, alimenté par la tension sinusoïdale
délivrée par un générateur basse fréquence.
Raccordez l'oscilloscope pour visualiser sur la voie 1 une tension proportionnelle
à l'intensité du courant traversant le circuit, et sur la
voie 2, la tension totale délivrée par le générateur
basse fréquence, ou mieux, la tension aux bornes de la diode.
Vous choisirez une fréquence de 1000 Hz et une amplitude de
2,5 V pour la tension sinusoïdale.
Représentez sur votre compte-rendu les courbes obtenues. Interprétez
ces courbes.
Haut de
cette page 
Programme
officiel de physique de première S. III Électrodynamique
B. Magnétisme, forces
électromagnétiques
EXEMPLES D'ACTIVITÉS
Étude documentaire sur l'histoire du magnétisme et de
l'électromagnétisme*.
Expérience de l'aimant brisé.
Comparaison de deux champs magnétiques.
Mise en œuvre d'expériences montrant les caractéristiques
du champ magnétique crée par :
- un courant rectiligne ;
- une bobine ou un solénoïde.
Comparaison du champ externe d'un solénoïde et celui d'un
barreau aimanté.
Mise en évidence du champ magnétique terrestre.
Utiliser la loi de Laplace pour interpréter qualitativement
des expériences telles que :
- barre mobile sur rails,
- action entre courants parallèles,
- mouvement d'une bobine au voisinage d'un aimant.
Mise en évidence du principe de fonctionnement d'un haut-parleur
électrodynamique, d'un moteur à courant continu. Observer
le fonctionnement en microphone d'un HP électrodynamique.
CONTENUS
1. Champ magnétique
Action d'un aimant, d'un courant continu, sur une très courte
aiguille aimantée. Vecteur champ magnétique 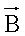 :
direction, sens, valeur et unité. Exemples de lignes de champ magnétique
; champ magnétique uniforme.
:
direction, sens, valeur et unité. Exemples de lignes de champ magnétique
; champ magnétique uniforme.
Superposition de deux champs magnétiques (addition vectorielle)
2. Champ magnétique créé par un courant Proportionnalité
de la valeur du champ Ê et de l'intensité du courant en l'absence
de milieux magnétiques.
Champ magnétique crée par : un courant rectiligne, un
solénoïde.
3. Forces électromagnétiques
Loi de Laplace ; direction, sens, valeur de la force : F=IlBsina.
4. Couplage électromécanique
Conversion d'énergie électrique en énergie mécanique.
Rôle moteur des forces de Laplace.
Observation de l'effet réciproque associé au mouvement
d'un circuit dans un champ magnétique : conversion d'énergie
mécanique en énergie électrique.
CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES
Une petite aiguille aimantée permet d'obtenir la direction et
le sens du champ magnétique dans une petite région de l'espace.
Les caractéristiques du vecteur champ magnétique. Réaliser
des spectres magnétiques.
Utiliser une sonde à effet Hall.
Les lignes de champ magnétique se referment sur elles-mêmes.
Connaître la topographie du champ magnétique créé
par : un courant rectiligne, un solénoïde.
Savoir que la valeur de 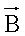 dépend
de la géométrie du courant, de son intensité ainsi
que du point de mesure. Appliquer la loi de Laplace pour évaluer
la force qui s'exerce sur une portion rectiligne de circuit.
dépend
de la géométrie du courant, de son intensité ainsi
que du point de mesure. Appliquer la loi de Laplace pour évaluer
la force qui s'exerce sur une portion rectiligne de circuit.
Sur un schéma de principe donné, représenter la
force de Laplace qui explicite le fonctionnement:
- d'un haut-parleur électrodynamique ;
- d'un moteur à courant continu.
Connaître les ordres de grandeur de la puissance des moteurs
électriques usuels.
Leçon 12 : Champ magnétique
12.1. Notion de champ magnétique
Au voisinage de la Terre, une aiguille aimantée, mobile autour
d'un axe vertical, ou boussole, s'oriente toujours dans la même direction
et le même sens. Les forces qui font tourner l'aiguille ont une origine
magnétique. On appelle pôle Nord de l'aiguille aimantée,
le pôle qui pointe vers un pôle magnétique de la Terre.
Ce pôle magnétique, proche du nord géographique, est
appelé à tort nord magnétique, car nous verrons qu'il
s'agit d'un Sud magnétique. L'autre pôle de l'aiguille est
appelé pôle Sud. La Terre crée un champ magnétique.
Un aimant aussi crée dans l'espace qui l'entoure un champ magnétique.
Si on approche deux aimants, leurs pôles de même nom
se repoussent, leurs pôles de nom contraire s'attirent.
12.2. Le vecteur champ magnétique
Un champ magnétique est caractérisé en chaque
point par un vecteur champ magnétique
-
qui a pour direction celle de l'aiguille aimantée placée
en ce point,
-
qui a pour sens celui de l'axe sud-nord de l'aiguille aimantée,
-
qui a une valeur B mesurée en tesla (symbole T).
Quelques ordres de grandeur : Champ magnétique terrestre 50 mT,
bobine supraconductrice d'une IRM 1 T.
Superposition de champs magnétiques : Ils s'ajoutent comme des
vecteurs.
12.3. Spectre magnétique
Des particules de limaille de fer répandues au voisinage
d'un aimant s'orientent dans l'espace, en dessinant des lignes. C'est un
spectre magnétique. Les lignes sont appelées lignes de champ.
Le vecteur champ magnétique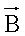 ,
leur est tangent en chaque point. Les lignes sont orientées dans
le sens de
,
leur est tangent en chaque point. Les lignes sont orientées dans
le sens de 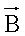 .
Ces lignes sortent du pôle Nord d'un aimant et convergent vers le
pôle Sud.
.
Ces lignes sortent du pôle Nord d'un aimant et convergent vers le
pôle Sud.
12.4. Champ magnétique uniforme
Entre les deux branches d'un aimant en U, les lignes de champ sont
parallèles. On peut montrer que dans cette région, le vecteur 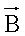 est
le même en tout point.
est
le même en tout point.
Dans un champ uniforme, le vecteur est le même en tous les points
; les lignes de champ sont des droites parallèles.
12.5. Champ magnétique terrestre
Pour tout retenir : Un pôle Nord attire un pôle Sud
Les lignes de champ sont orientées dans le sens Sud - Nord de la boussole qui explore le champ.
Située près du pôle Nord d'un aimant droit, la boussole lui présente
donc son pôle Sud. Donc, les lignes de champ sortent par le pôle Nord
de l'aimant droit et y rentrent par son pôle Sud.
Le pôle Nord de la boussole pointe vers le Nord magnétique terrestre.
Celui-ci est proche du pôle Nord géographique. ATTENTION donc, le Nord
magnétique terrestre n'est pas un pôle Nord d'aimant droit.
On peut donc considérer que le champ géomagnétique est semblable au
champ créé par un aimant droit, mais celui-ci serait inversé : Le pôle
Nord de l'aimant coïnciderait avec le pôle Sud magnétique terrestre.
En fait, cet aimant droit fait un angle de 11° par rapport à l'axe de
rotation de la Terre. Le Nord magnétique est proche du Nord
géographique, mais ne coïncide pas avec lui.
Le champ magnétique terrestre s'est inversé de nombreuses fois au cours du temps. La
trajectoire du pôle Nord magnétique terrestre n'est pas la même vue de
l'Europe, de l'Amérique du Nord ou de l'Inde. Ceci confirme l'hypothèse
de la tectonique des plaques.
12.6. Exercices
Pages 198 et suivantes, contrôler ses connaissances plus exercices
7 (lignes de champ), 13 (superposition de champs).
12.7. Travail pratique
12.7.1. Matériel, fiche pour le préparateur
Au bureau :
Aimants droits et autres aimants, boussoles et barreaux aimantés.
Pour 9 groupes d'élèves :
Boussole des tangentes
1 ampèremètre.
Alimentation.
12.7.2. Fiche élève
Travail pratique : Champ magnétique
1. Les champs magnétiques s'ajoutent vectoriellement
Placez au voisinage l'un de l'autre deux aimants droits et une boussole,
pour montrer que les champs magnétiques s'ajoutent vectoriellement.
Montrez votre installation au professeur.
2. Mesure du champ magnétique terrestre par la boussole des tangentes
Haut de cette
page 
Leçon 13 : Champ magnétique
créé par un courant
13.1. Un courant électrique crée un champ magnétique
Le physicien danois Oersted découvre cette propriété
en 1819, par hasard, pendant qu'il donne un cours de physique.
Tout circuit électrique parcouru par un courant crée
un champ magnétique. La valeur du champ en un point est proportionnelle
à l'intensité du courant, sauf en présence de matériaux
ferromagnétiques.
13.2. Champ magnétique créé par différents
circuits électriques
13.2.1. Courant rectiligne
Les lignes de champ sont des cercles centrés sur le fil.
Le vecteur champ magnétique 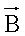 créé
en un point M est :
créé
en un point M est :
-
perpendiculaire au plan déterminé par le fil et le point
M ;
-
de sens donné par le bonhomme d'Ampère, ou la règle
des 3 doigts de la main droite.
Le bonhomme d'Ampère est couché sur le fil, le courant le
traverse en entrant par les pieds, il regarde le point M, il tend le bras
gauche qui donne le sens du vecteur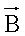 .
.
// S'il est foudroyé par la tête, il tend le bras droit
!
13.2.2. Bobine
Les lignes de champ sont similaires à celles produites par
un aimant droit. La règle du tire-bouchon donne le sens du champ
magnétique. Si on tourne le tire-bouchon comme tourne le courant
dans la bobine, le tire-bouchon avance dans le sens (Sud Nord) des lignes
de champ.
// Règle inconnue des pays anglo-saxons.
13.3. Champ magnétique créé par un solénoïde
Un solénoïde est une bobine droite, avec des enroulements
régulièrement répartis.
A l'intérieur d'un solénoïde long, le champ magnétique
est uniforme, dirigé selon l'axe du solénoïde.
A l'intérieur d'un solénoïde long, de longueur L,
comportant N spires, parcouru par un courant d'intensité I, le champ
magnétique vaut
m0 est la perméabilité
magnétique du vide et vaut par définition 4p
. 10-7 u. S.I.
Application : Solénoïde supraconducteur employé
dans les appareils d'imagerie par résonance magnétique nucléaire.
13.4. Électroaimants
Pour réaliser des champs intenses, de plusieurs teslas, on
emploie des bobines supraconductrices parcourues par des courants très
intenses (20 000 A), ou on introduit à l'intérieur d'une
bobine classique un matériau ferromagnétique (fer doux) qui
augmente la valeur du champ environ 1000 fois, mais de manière non
linéaire. On a réalisé un électroaimant.
13.5. Exercices
Page 198 et suivantes, exercices 10 (solénoïde), 11
(solénoïde, étalonnage du teslamètre), 14 (fils
parallèles), 19 (bobines de Helmholtz).
13.6. Travail pratique
13.6.1. Matériel, fiche pour le préparateur
Au bureau :
Solénoïde Jeulin de démonstration,
fils,
ampèremètre,
générateur puissant descendant à 0,
teslamètre et son voltmètre éventuel.
Alimentation Pierron, jaune et bleue,
différents circuits électriques,
limaille de fer,
feuilles de papier pour verser la limaille.
13.6.2. Fiche élève
Travail pratique : Étude du champ magnétique créé
par un solénoïde long
1. Le 0 du teslamètre doit être ajusté. Pourquoi ?
2. Relation entre la valeur du champ magnétique et l'intensité
du courant traversant le solénoïde.
3. Relation entre la valeur du champ magnétique et le nombre de
spires du solénoïde.
4. Relation entre la valeur du champ magnétique et la longueur du
solénoïde.
5. Relation entre la valeur du champ magnétique et le diamètre
du solénoïde.
6. Conclusion.
7. Critiquez la façon dont nous avons mesuré la perméabilité
magnétique du vide, m0.
Haut
de cette page 
leçon 14 : Forces électromagnétiques
14.1. Loi de Laplace
Expériences :
-
Bobine mobile placée au voisinage d'un aimant droit (champ magnétique
non uniforme).
-
Rails de Laplace.
-
Interaction entre deux fils parcourus par des courants de même sens
ou de sens contraire.
Un circuit électrique placé dans un champ magnétique
subit des forces électromagnétiques.
Force de Laplace : Une portion de fil rectiligne de longueur L, parcourue
par un courant d'intensité I et placée dans un champ magnétique 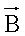 uniforme
est soumise à une force électromagnétique
uniforme
est soumise à une force électromagnétique
-
de direction perpendiculaire au plan déterminé par le fil
rectiligne et le vecteur champ
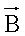 ,
,
-
de sens donné par le bonhomme d'Ampère,
-
de valeur F = B . I . L . sina, où a
est l'angle formé par le fil et le vecteur
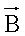 .
.
Le bonhomme d'Ampère est couché selon le fil, le courant
électrique le traverse par les pieds, le vecteur 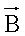 est
planté dans son dos (ou il regarde dans le sens de
est
planté dans son dos (ou il regarde dans le sens de 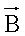 ),
la force de Laplace est vers sa gauche.
),
la force de Laplace est vers sa gauche.
14.2. Application : Le haut-parleur électrodynamique
Il comporte un aimant. dans l'entrefer de celui-ci est placée
une bobine mobile qui entraîne une membrane qui met en mouvement
l'air à son contact.
Le haut-parleur électrodynamique convertit une partie de l'énergie
électrique reçue en énergie mécanique. Il est
réversible : S'il reçoit de l'énergie mécanique,
il la convertit en énergie électrique ; il se comporte alors
comme un microphone.
14.3. Application : Le relais électromagnétique
Un petit électroaimant alimenté en basse tension (6
ou 12 V) actionne un interrupteur mécanique auquel est relié
un circuit électrique en moyenne tension.
14.4. Application : Le moteur électrique
Un des nombreux modèles comporte un rotor, bobine traversée
par un courant électrique, tournant dans l'entrefer d'un aimant
fixe, stator. Lorsque la bobine pénètre dans une zone où
le champ magnétique change de sens, on change aussi le sens du courant
dans la bobine, pour qu'elle poursuive sa rotation.
14.5. L'alternateur
C'est l'application réciproque. La variation du champ magnétique
qui baigne une bobine produit l'apparition aux bornes de celle-ci d'une
tension électrique induite. C'est le phénomène d'induction
électromagnétique.
L'alternateur convertit l'énergie mécanique en énergie
électrique.
14.6. Exercices
Page 214 et suivantes, exercices 4 (direction des forces de Laplace),
8, 15 (haut-parleur), 16 (moteur électrique).
14.7. Travail pratique
14.7.1. Matériel, fiche pour le préparateur
Pour 9 groupes d'élèves :
Haut-parleur
fils,
multimètre,
générateur ELC jaune, descendant à 0,
boîte de masses marquées,
générateur basse fréquence,
prise BNC, rhéostat.
14.7.2. Fiche élève
Travail pratique : Étude d'un haut-parleur électrodynamique
Le but de ce travail pratique est de déterminer quelques
caractéristiques d'un petit haut-parleur.
Ce haut-parleur ne peut pas dissiper une puissance électrique
supérieure à 5 watts. Mesurez sa résistance (nous
supposerons qu'elle est égale à son impédance que
vous trouverez inscrite sur le haut-parleur). Calculez l'intensité
maximale que peut supporter la bobine du haut-parleur.
Vous ne devrez jamais dépasser cette intensité.
Branchez en série avec le haut-parleur un rhéostat de
protection.
Faites vérifier votre montage par le professeur.
Mesurez la force F exercée sur la membrane du haut-parleur par
la bobine, pour 5 valeurs d'intensité I, de 0 A jusqu'à 70
% de l'intensité maximale.
Représentez graphiquement la loi reliant I à F.
Raccordez le haut-parleur au générateur basse fréquence
et déterminez grossièrement la bande passante en fréquence
du haut-parleur.
Haut de
cette page 