Étude des sons et des vibrations, transformées de Fourier, fenêtres, sonagrammes

Page modifiée le 16 mai 2008. NOUVEAU : Améliorations importantes de WaveFFT, version 21 . 4, FFT sur 2 millions de points, filtrage de fréquences par F11, création de fichiers Wave superposition d'un nombre illimité de sinusoïdes par F12.

Logiciels, page 2, sommaire : Un logiciel cours sur la FFT , le cours livré avec ce logiciel, des fichiers de sons au format Wave, pour vos travaux pratiques (MPI, spécialité physique de terminale S).

Descriptif rapide :

2 logiciels, dont 1 obsolète, sont disponibles :

1°Un logiciel cours sur la FFT. Il comporte un cours interactif (si celui-ci pose problème, voir le 2° et le cours ne sera pas interactif) et permet l'étude des séries et des intégrales numériques de Fourier, avec de nombreuses fenêtres.
Il simule, il traite les fichiers sons au format Wave, il ne pilote plus les cartes Candibus ; il accepte les autres données par Copier | Coller. Il réalise des sonagrammes et peut échanger des données avec les tableurs, les logiciels de calcul formel Mathematica et Maple, ainsi que des images de sonagrammes avec tout logiciel de dessin.
Compatible Win 95, Win 98, Win Millénium. Compatibilité testée avec Win XP y compris Professionnel (en cas de problème créé par le réseau - fausse division par 0 -, se connecter en mode administrateur).

2° Dans le cas où le logiciel ne peut lancer le navigateur incorporé, le texte de l'aide, au format HTML, pourra être consulté, de manière non interactive, avec Netscape Navigator, Opera, Mozilla ou IE.

Le logiciel après décompression est nommé waveFFT.exe, avec son aide au format Html, dans le sous-dossier waveFFT \ Html. C'est la version récente, entièrement gratuite,

Et l'ancêtre :

3°Vibr.exe, c'est la version ancienne, maintenant obsolète (qui ne peut pas lire tous les fichiers Wave, notamment ceux comportant un Copyright, qui affiche trop sommairement les résultats de la FFT... ).

Haut de la page

Logiciel cours sur la FFT, waveFFT_z_.exe (les _ correspondent à des numéros de versions), donne après décompression waveFFT.exe : description, extrait du cours et de l'aide associés

waveFFT_z_.exe est bien plus performant que son ancêtre Vibr.exe :

• il comporte une partie simulation :

simulation de somme de sinusoïdes (5 au maximum), de triangles, créneaux,

Nouveau : création de fichiers Wave simulés par addition d'un nombre illimité de sinusoïdes,


• simulations de distorsions diverses, appliquées aux sommes de sinusoïdes.

• et une partie traitement de mesures. Il lit les fichiers Wave 8 ou 16 bits (mono ou stéréo, mais sur 1 seul canal à la fois). Il  peut importer une colonne de mesures depuis un tableur, ce qui permet d'exploiter les mesures de cartes d'acquisition.

Il peut appliquer à ces valeurs des décompositions en série de Fourier, avec possibilité de reconstruction graphique en ne retenant que les premiers termes (jusqu'à 50 termes), ou de reconstruction d'un fichier wave qui pourra être écouté pour comparaison à l'original. Ces calculs de séries de Fourier permettent une mesure précise de la fréquence (ce qui n'est pas toujours le cas des logiciels concurents). Les résultats de ces calculs, fréquences et amplitudes des harmoniques, sont transférables dans Excel, Calc ou tout autre tableur par simple Copier | Coller.
• Il peut aussi appliquer sur un nombre maximal - Nouveau - de 2 millions de points (2 097 152 exactement), une transformée de Fourier (intégrale) numérique ou FFT. Celle-ci est rapide si le nombre de points retenu est une puissance de 2 ; autrement, au-dessous de 4 096 points, le calcul est possible, mais plus long. De nombreuses fenêtres, elles-mêmes visualisées, peuvent être appliquées (Rectangulaire, Hamming, Blackman, Hanning ou von Hann, Triangulaire, Bartlett, Bartlett - Hann, Blackman - Harris, Gauss, Nuttall, Flat Top ou Flattop, exponentielle, Kaiser - Bessel, Chebyshev, Kpark, Rife-Vincent à 2, 3, 4 ou 5 termes).
• Les résultats de ces calculs de FFT, fréquences et modules, ou fréquences et parties imaginaires et réelles, sont transférables dans Excel, Calc ou tout autre tableur par simple Copier | Coller.
• Il peut diminuer la résolution de l'échantillonnage d'un fichier Wave, de 16 jusqu'à 2 bits, ainsi que sa fréquence d'échantillonnage.
• Nouveau : Il permet enfin le filtrage de Fourier, jusqu'à 50 bandes de fréquences à la fois, avec visualistion du spectre filtré et possibilité de créer un fichier Wave filtré. Le nombre de points doit être une puissance de 2, jusqu'à 2 097 152 points.

De plus, il peut créer, à partir d'un fichier .wave (mono ou stéréo, 8 ou 16 bits), un fichier .txt lisible (le code nécessaire est fourni dans l'aide en ligne ainsi que plus loin sur cette page) par Mathematica ou Maple. Si le Wave est stéréo, il est décomposé en deux fichiers G et D, comportant les entiers mesurés sur les canaux Gauche et Droit. La fréquence d'échantillonnage qui s'affiche doit être transférée "à la main" dans Mathematicaou Maple. En effet, Mathematica (version 3) n'est pas capable de lire un fichier Wave sur 16 bits, ce qui est regrettable (il s'agit d'une "petite" méchanceté de Microsoft - une de plus - que j'ai dû contourner moi-même pour créer WaveFFT qui lit directement les Wave sans passer par Bill)

Lors de la comparaison (graphique et auditive) entre le signal original et la reconstitution de sa série de Fourier,

• vous pouvez choisir le nombre des premiers harmoniques retenus (maximum 50) trouvés par analyse de Fourier. En ce cas, il veille à commencer et terminer les fichiers sonores Wave reconstitués sur des tensions nulles, ce qui permet une écoute en boucle parfaite, à supposer que votre lecteur soit rapide, ce qui était le cas d'anciennes versions de MediaPlayer, mais pas celui des nouveaux lecteurs gadgets de Windows. Notez que les nouvelles versions se contentent de lancer les anciennes (qui sont donc toujours présentes dans Windows), en les habillant de gadgets et en les ralentissant. Rechercher les versions anciennes plus rapides, par exemple dans "C:\Program Files\Windows Media Player\mplayer2.exe" et placez en un raccourci sur le bureau. Mediaplayer peut lire un fichier en boucle, de façon parfaite et vous pouvez en lancer plusieurs versions en simultané, avec des sons différents.
• vous pouvez ajouter aux sons précédents des effets de vibrato ou de trémolo ;

Ce logiciel est capable de tracer des sonagrammes, en 32 niveaux de noir et blanc, ou en 32 couleurs,  personnalisables et sauvegardables. Pour chaque sonagramme,  vous pouvez :

• Choisir le nombre de points de chaque FFT, puissance de 2, jusqu'à 4096,
• choisir le fenêtrage des FFT, choisir l'échelle, linéaire ou logarithmique,
• choisir, au cas où vous calculez une FFT sur de nombreux points, la zone du spectre représentée, Basse, Bas médium, Haut médium, ou Haute,
• choisir de sauter ou pas des points lors des FFT, pour améliorer la résolution en fréquence,
• choisir la résolution temporelle en fixant le nombre d'échantillons sonores d'avance entre 2 FFT successives.
• Copier le sonagramme obtenu, puis le Coller dans un logiciel de dessin.
• Enregistrer le sonagramme sous forme de bitmap.

Ce logiciel permet aussi de lire les fichiers au format texte .Txt, ou texte enrichi, .Rtf (réalisables à l'aide de Notepad, WordPad, Write, Word, ClarisWorks...), ce qui permet d'y ajouter facilement des fiches de travaux pratiques (non interactives).

Ce logiciel vous rendra de grands services car il

• convient au programme de spécialité physique de terminale S (spectres sonores, sonagrammes),
• peut être employé en travaux pratiques de Mesures Physiques et Informatique (étude de l'échantillonnage, des sons),
• convient à de nombreux sujets de Travaux Personnels Encadrés de terminale S, de TIPE de l'enseignement supérieur,
• être employé de manière plus générale pour étudier les sons ou les vibrations.
• Plusieurs entreprises françaises l'utilisent pour accorder des instruments, étudier le rebond de tables de billard...

Si vous avez rédigé un superbe TP (le texte non formaté et les paramètres choisis suffisent) associé à ce logiciel, n'hésitez-pas à nous le communiquer ; nous l'ajouterons (avec vos références) aux fichiers Html. N'hésitez-pas non plus à nous faire part de vos suggestions.
 
 

Logiciels Freeware (graticiels). WaveFFT22z0.exe. La toute dernière version 22.0. FFT jusqu'à 2 097 152 points, filtrage de Fourier. waveFFT21z4.exe La version précédente. FFT jusqu'à 2 097 152 points, filtrage de Fourier. waveFFTl19z6.exe La dernière version, light, allégée de son navigateur qui cause parfois des erreurs OLE, avec Wave test   Anciennes versions : waveFFT19z1.exe Une précédente version waveFFTl19z1.exe Une précédente version, light, allégée de son navigateur qui cause parfois des erreurs OLE

 

Modifié à de nombreuses reprises, pour satisfaire des besoins divers (TPE, cours de spécialité physique, Olympiades de Physique, TIPE...), ce logiciel manquait d'ergonomie. Il a été entièrement réécrit, pour être plus rapide, plus simple d'emploi et compatible avec Win XP. Il ne pilote plus les cartes Candibus. Si vous y découvrez un bug, merci de le signaler à l'auteur.

Après décompression, l'exécutable rangé dans C:\Program Files\PhyJi\Physique, se nomme waveFFT et le cours est rangé dans le sous-dossier C:\Program Files\PhyJi\Physique\waveFFT\HTML.

Haut de la page

Plus d'informations, aperçu du cours

Fichiers sonores :

Pour travailler immédiatement avec ces deux versions, voici quelques dossiers contenant des fichiers .Wave, livrés chacun avec un petit texte explicatif, au format .txt, lisible par tout traitement de texte, et directement par ce logiciel de traitement du son et des vibrations.

Des enregistrements du piano personnel de l'auteur, malheureusement accordé depuis plus d'un an ; le la3 du diapason de notre laboratoire ; quelques sons de percussion, issus de la banque de sons d'une carte Sound Blaster ; dossier de 3,7 Mo de divers instruments joués par des élèves (ce sont eux qui ont accordé leur intrument et ont proposé le nom des notes), flûte à bec, flûte traversière, hautbois, violon, harmonica, didgeridoo (instrument des Aborigènes d'Australie, construit ici avec un tube en PVC), guitare sèche, guitare électrique, basse électrique, voix chantée (garçon en pleine mue !). Des erreurs se sont glissées dans le nom des notes donnés par les élèves ; ce travail pratique (avec corrigé), vous propose de retrouver ces erreurs.

Nouveau : Quelques enregistrements complémentaires qui se rangeront automatiquement dans le dossier des précédents : Une boîte à musique tenue à la main (et quasiment inaudible) et posée sur une caisse de résonance (table en bois = table d'harmonie ou adaptateur d'impédance, plutôt que caisse de résonance), grenouille en bois de Guadeloupe, tenue à la main ou posée sur une caisse de résonance (curieusement, c'est tenue dans la main qu'elle émet le son le plus fort et réaliste). Un travail pratique de filtrage de fréquences, livré avec le texte du TP, le fichier son original et deux fichiers filtrés en guise de corrigé. Il s'agit d'éliminer le bruit d'une mobylette qui masque le chant d'un merle. Si on élimine le chant du merle, on entend la mobylette et des grillons que le chant du merle masquait.

2 enregistrements (biseau de flûte et flûte) pour étudier la production d'un son (Programme de spécialité physique de terminale S).

Un enregistrement permettant de détecter le passage de météorites, réalisé de la manière suivante : Un récepteur FM, muni d'une antenne directive, est accordé sur un émetteur trop lointain pour être reçu, on n'enregistre donc que du bruit. Lorsque des météorites pénètrent dans l'atmosphère, celle-ci est ionisée et se comporte alors comme une antenne relais. Des bribes de musique sont enregistrées, au-milieu d'un bruit de fond. Ce son peut être écouté ; un sonagramme permet de distinguer le bruit de la musique. Ce projet a été approfondi, avec les collègues de sciences de la vie et de la Terre, voir le chapitre Olympiades de la physique.

Nous vous conseillons de décompresser ces fichiers, sans changer le chemin proposé ; ainsi tout sera rangé au bon endroit.

Voici un exemple de fenêtre Windows personnalisée obtenue :

 
 

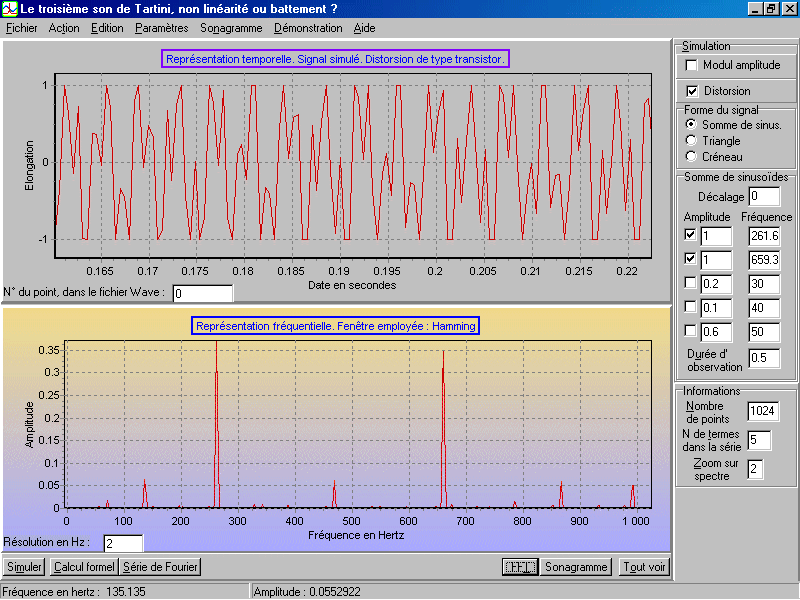
Vibr.exe L'ancêtre Maintenant totalement obsolète, remplacé par waveFFT.exe	Étude des vibrations avec une carte son, traitement des fichiers .Wav, FFT (sur un nombre quelconque raisonnable de points), transfert dans Excel, Maple, Mathematica, freeware. Livré avec son aide en ligne (ne vous inquiétez-pas du message d'erreur) comportant des idées de travaux pratiques. Attention, pas parfait ce logiciel, car réalisé pour une Olympiade de Physique, donc dans le but de traiter un problème limité. Il ne peut pas lire les fichiers Wave comportant un Copyright.	Traite les fichiers .Wav donnés par les cartes son des ordinateurs (8 ou 16 bits), élimine à la demande un certain nombre de points, calcule et trace leur spectre de Fourier et transfère toutes les valeurs numériques dans Excel, Mathematica et Maple. Vous trouverez toutes informations à son sujet dans le chapitre Olympiades, page 1. Si vous programmez en Delphi, vous pouvez ne charger que son code source (pas parfait, mais commenté, qui vous appoertera des informations sur le traitement de fichiers Wave, la FFT).
	Chargement Vibr.exe  Voyez plutôt waveFFT.exe	vibrcode.exe, code source Delphi de Vibr.exe

Haut de la page
 

Voici un extrait du cours associé au logiciel WaveFFT.exe.

Le cours est composé de trois pages.

La première page s'appuie sur des simulations ; elle aborde la série et l'intégrale de Fourier.

La deuxième pousse l'étude un peu plus loin, entre autres sur les artefacts apportés par les approximations numériques, lors d'une transformation de Fourier de type FFT.

La troisième donne quelques informations sur les relations mathématiques employées pour calculer les séries et intégrales de Fourier de manière formelle, ainsi que sur les calculs numériques approchés appliqués lorsque la tension à transformer est mesurée à des intervalles de temps réguliers (échantillonnée) et donc donnée sous forme d'un tableau de valeurs numériques.

L'aide et le cours joints au logiciel sont au format Html, employés pour construire des sites Internet. Vous pouvez y adjoindre des démonstrations ou travaux pratiques personnalisés. Pour cela l'aide comporte une page de modèles avec des boutons Html, déclenchant diverses actions, accompagnés de leur mode d'emploi.

Haut de cette page
 
 

Quelques points mathématiques.

Petit cours sur la transformation de Fourier, à l'usage du physicien débutant et de quelques autres.

Sommaire : Développement d'une fonction périodique en série de Fourier ; développement d'une fonction non périodique en intégrale de Fourier ; transformation de Fourier (numérique) rapide, ou FFT ; transformation numérique, quand est-elle rapide ? ; transférer des fichiers sonores Wave dans Mathematica et Maple.

Fenêtrages

1.1. Conditions que doit remplir la fonction f(t)

1.2. Écriture de la fonction f(t)

1.3. Calcul des coefficients a_i et b_i

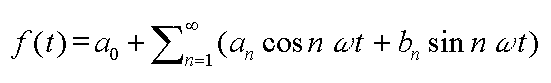
le premier terme, a₀ est donné par :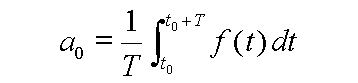 

les suivants par 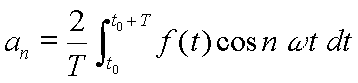 et

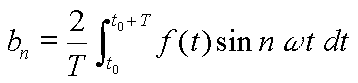
Si la fonction f(t) est paire, les coefficients b_n des sinus sont nuls, puisque la fonction cosinus est paire, la fonction sinus impaire.
 

Sinus et cosinus de même pulsation peuvent être regroupés sous forme d'un sinus (ou d'un cosinus) comportant en plus un terme de phase.

1.4. Exemple, développement en série de Fourier d'une fonction créneaux de fréquence f et d'amplitude U

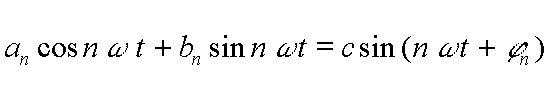
On peut démontrer, par calcul formel, que cette fonction (moyennant certaines restrictions dues au fait qu'elle est discontinue) peut s'écrire comme la somme de termes de fréquences f, 3 f, 5 f, 7 f... (les harmoniques de rang pair sont absents, ou d'amplitude nulle, ce qui ne doit pas être confondu avec la parité ou non parité éventuelle de la fonction). Les amplitudes de ces harmoniques sont Y = 4 U / Pi, Y / 3, Y / 5, Y / 7...

Haut de la partie mathématiques

1.5. Calculs effectués par ce logiciel

Le logiciel associé à ce cours calcule la fréquence, l'amplitude c_n et le terme de phase de chaque terme en sinus de la série de Fourier. Le carré de cette amplitude c_n est égal à la somme des carrés de a_n et b_n.
 

 Le premier terme de la série, a₀ correspond à la moyenne de la fonction f(t) sur une période (ou sur une durée infinie). Pour le physicien, ce terme correspond au décalage du zéro.

c₁ est l'amplitude du premier harmonique, ou fondamental, de fréquence 1 / T. c_n est l'amplitude du n^ème harmonique, de fréquence n / T.

Les calculs se font (sommairement) de la manière suivante : recherche de la période, intégration selon les relations précédentes, de manière numérique, donc approchée, en employant la méthode de Simpson. D'autres algorithmes seraient possibles.
 

La série peut aussi s'écrire, en employant les exponentielles complexes.
 
 
 

2 Développement d'une fonction non périodique en intégrale de Fourier

Une fonction non périodique (cela conviendrait aussi pour un fonction périodique) f  de carré sommable est égale à l'intégrale d'une fonction sinusoïdale qui peut s'écrire :

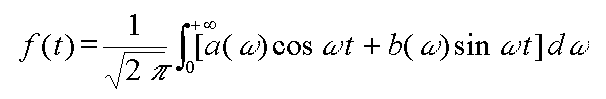
Là encore, il est possible de regrouper cosinus et sinus.
En employant les exponentielles complexes, l'expression devient :

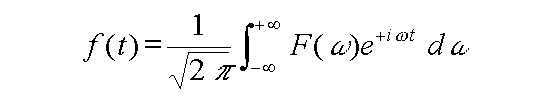
La fonction F(w) se calcule de la manière suivante :

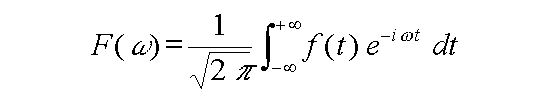
On notera la symétrie des calculs permettant de passer de f(t) à F(w). La deuxième est la transformée de Fourier de la première ; la première est la transformée inverse de la seconde.

Selon les branches de la physique, électronique, optique... et pour des raisons de commodité, des définitions différentes peuvent être adoptées. Cela revient à calculer de manière différente l'amplitude de la transformée de Fourier, ou à faire 'tourner à l'envers, +i devenant -i' le système oscillant considéré, ce qui n'a souvent aucune importance.

Le lecteur souhaitant approfondir cette question pourra effectuer des recherches sur les mots clés suivants : formule de Parceval, Parceval Plancherel.

Haut de la partie mathématiques
 
 

3 Transformation de Fourier (numérique) rapide, ou FFT

Souvent, le physicien ne dispose pas d'une fonction mathématique permettant une intégration par calcul formel, mais d'une série de mesures effectuées à des intervalles de temps réguliers. De plus, la durée de la mesure ne s'étend pas de zéro à l'infini.

Il lui faudra alors procéder à un calcul numérique (donc approché), sur une durée, donc un nombre de points de mesure finis. C'est un peu comme s'il observait un paysage infini, à travers une fenêtre finie. La formule de calcul est :
 

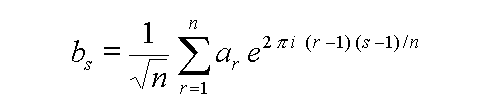
Cette formule peut différer d'un logiciel de mathématique à un autre. On ne peut affirmer que le résultat obtenu à l'aide de cette relation soit exact, mais dans tous les cas, la transformation inverse redonne la série de mesures d'origine.

Des artefacts se produisent, d'une part à cause des 'trous' existant entre deux points de mesure (risque de repliement de spectre) et d'autre part à cause de la durée finie de la mesure (effet de fenêtre).
Le lecteur souhaitant approfondir cette question pourra effectuer des recherches sur les mots clés suivants : FFT, fenêtrage, Hamming, Hanning, rectangulaire, flat top...

La fenêtre rectangulaire (mesures traitées par FFT, sans modification) est réputée idéale pour l'analyse des transitoires, la fenêtre de Hanning pour la résolution de fréquence, la fenêtre Flat Top pour la précision de l'amplitude.
 
 
 
 

4 Transformation numérique, quand est-elle rapide ?

La relation précédente montre que le calcul de chaque points du spectre en fréquence nécessite de multiplier chaque valeur mesurée par un sinus et un cosinus. Ainsi, 1000 points de mesure donnent un spectre comportant 1000 points, soit deux millions de calculs trigonométriques. La durée de calcul devient vite rédhibitoire, surtout pour une FFT en deux dimensions.
 

Lorsque le nombre de mesures est une puissance de 2 (128, 256, 512, 1024... ), des astuces de calcul permettent, par une sorte de 'mixage' dans le tableau de valeurs de limiter le nombre de calculs, donc la durée d'obtention du résultat.

En informatique (coprocesseur mathématique pour PC), l'emploi de la fonction SinCos, qui calcule simultanément sinus et cosinus d'un angle permet de gagner 30 % en vitesse de calcul.

Haut de la partie mathématiques
 
 

5 Transférer des fichiers sonores Wave dans Mathematica et Maple

5.1. Mathematica

Voici un exemple de programme permettant de récupérer le fichier tmp0, ou tmp1, ou tmp2... dans Mathematica. Ce fichier a été enregistré, à partir du logiciel lié à ce cours, dans un format texte, d'extension .txt. La fréquence d'échantillonnage est entrée 'à la main' dans Mathematica. Le logiciel lié à ce cours permet aussi de sauvegarder des couples date, tension, mais après lecture dans Mathematica, il faudra les séparer. Vous pourriez utilement consulter l'ouvrage "Problèmes pour physiciens, résolus avec Mathematica et Maple", aux éditions Ellipses, écrit par l'auteur de ce logiciel.
 

ClearAll["Global`*"];
adresse="C:\\Mesdoc\\Olympiades\\Sons\\tmp0";

 Employez des doubles barres de fraction inversées \\, car en Mathematica, comme dans le langage C, \ suivie d'une lettre peut être le code d'une instruction.

L'adresse du fichier doit être donnée 'à la main'. Soyez très attentifs à l'orthographe.

suite =  ReadList[adresse, Number];
nPoints=Length[suite]
suiteCourte = Drop[suite,Ceiling[0.1 nPoints]];
suiteCourte = Drop[suiteCourte,-Ceiling[0.85 nPoints]];
ListPlot[suite, PlotJoined->True, PlotRange->All];
ListPlot[suiteCourte, PlotJoined->True, PlotRange->All];
(* ListPlot[suite, PlotJoined->True, PlotRange->{All,{-32768,+32767}}]; *)

amplitude=Abs[Fourier[suite]];
freqEchant=11025 ;nPointsSpectre=Ceiling[nPoints/2]
liste=Table[{((i-1)freqEchant)/Length[suite],amplitude[[i]]},{i,
      nPointsSpectre}];

ListPlot[liste, PlotJoined->True, PlotRange->All, ImageSize->{500,300}];
 

listeCourte= Drop[liste,-Ceiling[0.9  nPointsSpectre]];
listeCourte= Drop[listeCourte,Ceiling[0.  nPointsSpectre]];
Length[listeCourte]
ListPlot[listeCourte, PlotJoined->True, PlotRange->All, ImageSize->{500,300}];

Drop permet de tronquer les listes.
Les points virgules évitent l'affichage des longues listes.
 
 

5.2. Maple

Pour Maple, les différentes mesures sont séparées par des retours chariot #10.

Voici le code Maple, permettant de traiter une liste de mesures .Wav, converties par le logiciel 'Vibrations' ou le logiciel associé à ce cours : Vous pourrez ainsi représenter graphiquement l'évolution de la tension au cours du temps, et tracer son spectre de Fourier, par F.F.T.

> restart;
> Adresse:=`C:/Tempo/Tmp1` :

Ceci initialise Maple, auquel, nous donnons ensuite l'adresse du fichier de nombres créé par notre logiciel 'Vibrations'.
Vibrations range le fichier converti, sous le nom tmp1, tmp2 ... dans le dossier contenant les fichiers sons .Wav à convertir.

Notez les accents graves, obtenus avec les touches Alt Gr et 7 pressées simultanément, suivies d'un appui sur la barre
d'espacement, ainsi que les barres de division.

> longueurFichier:=filepos(Adresse,infinity);

                        longueurFichier := 579

Ceci nous donne la taille en octets du fichier, mais place le pointeur en fin dudit fichier. Nous initialisons à nouveau :

> restart;Adresse:=`C:/Tempo/Tmp1` : frequenceEchant := 25 :
> tableauMesures:=array(1..256) :
> for i from 1 to 256 do nombreLu:=readline(Adresse) ; tableauMesures[i]:=[i/frequenceEchant,op(sscanf(nombreLu,`%f`))] :
od:

Nous donnons à Maple, la fréquence d'échantillonnage, 25 Hz, 'à la main', car le fichier ne contient que les mesures.

> listeCouplesLue:=convert(tableauMesures, `list`):
> plot(listeCouplesLue):

Remarquer les nécessités de conversion de types, en Maple. (Pour Mathematica, tout est liste).

Passons maintenant à la transformation de Fourier. Maple propose une transformation numérique, rapide, ou FFT, uniquement
pour un nombre de points de mesure qui soit une puissance de 2. Mathematica effectue des FFT, sur un nombre quelconque
de points. Notre logiciel 'Vibrations' effectue des FFT sur un nombre de points, puissance de 2 ; mais il accepte aussi de

calculer une transformée numérique de Fourier sur un nombre quelconque de points (pas trop grand). En ce cas, il adopte une
méthode de calcul 'lente'.

Nous devons fournir à Maple l'exposant du nombre 2, ici 8 pour une FFT sur 256 points. Nous devons lui donner deux
tableaux de nombres, l'un contenant les valeurs imaginaires de nos mesures, ici des 0, l'autre, les valeurs réelles, c'est à dire nos
mesures. Compte tenu du fait que, plus haut, nous avons créé une liste de couples lue, formée des dates de mesure (calculées)

et des tensions mesurées, nous devons récupérer à chaque fois, le deuxième terme de chaque couple.

> exposant := 8 : longueur := 2^exposant :
> listeImaginaires := array([seq(0, i=1..longueur)]) :
> listeReels := array([seq(listeCouplesLue[i,2], i=1..longueur)]) :
> readlib(FFT) :
> FFT(exposant, listeReels, listeImaginaires) :

Nous chargeons une librairie FFT, et effectuons la transformation rapide. Les : évitent l'affichage de toutes les valeurs. Lorsque

nous souhaitons les voir pour tester notre code, la ligne doit se terminer par un ;.
A ce stade, Maple a rangé dans nos deux tableaux initiaux, les parties imaginaires et réelles obtenues par FFT.
Nous formons un tableau comportant les fréquences successives correspondant aux points du spectre, puis construisons un
tableau de couples (fréquence, module de la FFT). Il ne nous reste plus qu'à tracer le spectre.

> dureeEnregistrement := longueur/frequenceEchant :
> listeFrequences := array([seq((i-1)/dureeEnregistrement, i=1..longueur)]) :

> tableauSpectre := NULL :
> for k from 1 to longueur/2 do tableauSpectre := tableauSpectre, [listeFrequences[k], sqrt(listeReels[k]^2 +
listeImaginaires[k]^2)] : od :
> plot([tableauSpectre]) ;

Haut de la partie mathématiques

Haut de cette page
 

Fenêtrage dans une FFT

Index : Fenêtres rectangulaire, Flat Top ou Flattop, Blackman, Gauss, Nuttall,triangulaire, Tukey, Hamming, von Hann ou Hanning, Bartlett, Bartlett-Hann, Blackman-Harris, Bohman ; exponentielle, Kaiser, Chebyshev ou Tchebitchev ou Dolph-Chebyshev, influence de la fenêtre sur la résolution en fréquence, sur les artefacts et la résolution en amplitude ;

Remarque importante : Ce document a été réalisé en partant de diverses sources, notices de constructeurs, de fabricants de systèmes d'acquisition et de traitement des données, cours universitaires. Il nous a fallu jongler entre les diverses notations ; nous espérons y être parvenu. Cependant, des erreurs ont pu s'y glisser ; veuillez avoir l'obligeance de nous les signaler.

La FFT (Fast Fourier Transform) est une approximation numérique de l'intégrale de Fourier, approximation pour deux raisons : La fonction à transformer n'est pas connue sur l'intervalle ]- µ, + µ[ et d'autre part, elle n'est connue qu'en certains points, correspondants aux dates de mesure. Elle peut être rendue plus rapide si le nombre n de points de mesure est une puissance du nombre 2. Certains logiciels, tel Mathematica, sont capables de décomposer le nombre n en un produit de facteurs premiers, pour accélérer les calculs, lorsque n n'est pas puissance de 2.

Les coefficients numériques appliqués lors d'une FFT peuvent varier d'une application à l'autre, Mathematica, Maple, MatLab, selon que l'on considère des amplitudes ou des puissances. Nous nous sommes inspirés de Mathematica, mais avons dû modifier nos coefficients, pour obtenir des résultats plus réalistes.

Mais calculer sur un nombre fini n de points plutôt que de moins l'infini à plus l'infini, revient à appliquer une fenêtre, sur la suite supposée infinie de mesures. Ce fenêtrage modifie le spectre en fréquence obtenu.

La fenêtre la plus simple est appelée fenêtre rectangulaire.

Fenêtre rectangulaire

Elle consiste à garder les n points de mesure inchangés, et donc à considérer qu'en dehors, les mesures sont nulles. Cela revient à multiplier un hypothétique tableau infini de mesures par le coefficient w[k], avec :

w[k] = 0 si k < 0 ou k > n - 1 et

w[k] = 1 si k appartient à l'intervalle [0, n - 1]

Ici, nous supposons que les n points de mesure vont de k = 0 à k = n - 1.

Cette fenêtre rectangulaire est utilisée pour l'étude des signaux transitoires (signaux dont la durée est limitée), dont la durée est inférieure à celle de la fenêtre. Elle est aussi employée pour la recherche d'ordres, avec une fréquence d'échantillonnage proportionnelle à la vitesse de rotation des machines tournantes, ainsi que pour l'analyse de systèmes par l'étude de réponses à des excitations pseudo aléatoires. Elle peut servir à la séparation de 2 sons de fréquences proches, mais d'amplitude voisine.

Veuillez noter que pour procéder à une expérimentation par simulation, il faut choisir diverses fréquences pour les signaux sinusoïdaux. En effet, supposons que pour les paramètres choisis, le logiciel wavefft_z_.exe donnant WaveFFT.exe, indique une résolution de FFT de 0,2 Hz. Si vous choisissez un signal simulé à 10 Hzou 10,2 Hz, la FFT avec fenêtre rectangulaire semblera parfaite ; mais si vous prenez 10,1Hz, vous obtiendrez un résultat nettement moins bon. Donc, soit vous connaissez parfaitement la fréquence du signal à acquérir, et à condition de synchroniser l'acquisition à ce signal, la FFT avec fenêtre rectangulaire conviendra parfaitement, soit vous n'êtes pas dans ce cas et d'autres fenêtres seront alors préférables.

Aller à l'ensemble des fenêtres

Haut de la page

Fenêtre Flat Top ou Flattop

Veuillez noter que Flat Top est un terme générique ; il existe différents types de Flat Top, avec des coefficients différents.
Cette fenêtre donne une moins bonne résolution réelle en fréquence que la fenêtre de Hanning ; par contre, elle permet une mesure précise de l'amplitude d'un signal sinusoïdal, même si la fréquence de celui-ci se trouve entre 2 valeurs des fréquences obtenues dans le spectre de Fourier, par FFT. Elle est employée dans l'étalonnage des transducteurs, pour augmenter la précision de la mesure d'amplitude.

Pour cette fenêtre, le coefficient w est calculé ainsi :

w[k] = a₀ - a₁ cos(2 pk / n) - a₂ cos(4 p k / n), avec

k appartenant à l'intervalle [0, n] avec :

a0  = 0,2810638602 ; a1 = 0,5208971735 ; a2  = 0,1980389663.

Fenêtre de Blackman

Pour cette fenêtre, le coefficient w est calculé ainsi :

ce qui donne une fenêtre :

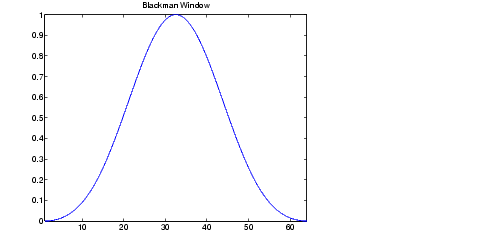
Aller à l'ensemble des fenêtres

Fenêtre de Gauss

Pour cette fenêtre, le coefficient w est calculé ainsi :

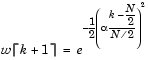
(Notez une erreur dans cette relation ; l'argument de l'exponentielle doit être négatif)

où  et . a est la réciproque de la déviation standard.

ce qui donne une fenêtre :

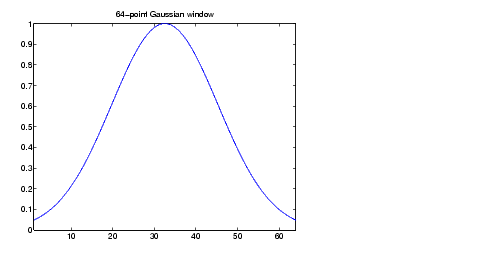
La largeur de la fenêtre est en raison inverse de la valeur de a.
Notez que l'intégrale de Fourier d'une gaussienne est une gaussienne. Les valeurs habituelles pour a sont 2,5 ou 3.

Fenêtre de Nuttall

Pour cette fenêtre, le coefficient w est calculé ainsi :

avec et

a₀ = 0,3635819 ; a₁ = 0,4891775 ; a₂ = 0,1365995 ; a₃ = 0,0106411.

ce qui donne une fenêtre :

Cette fenêtre minimise une fenêtre de Blackman-Harris à 4 termes. C'est à dire que le maximum des lobes latéraux est minimisé. Les coefficients sont différents de ceux de la fenêtre de Blackman-Harris.

Voici représentée la différence, inférieure à 0,01, entre ces deux fenêtres :

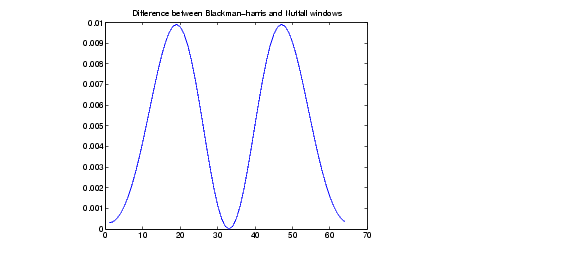
Aller à l'ensemble des fenêtres

Haut de la page

Fenêtre triangulaire

Pour cette fenêtre, le coefficient w est calculé ainsi :
Pour n impair :

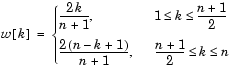
pour n pair :

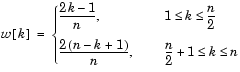
Elle est très similaire à la fenêtre de Bartlett, bien que contrairement à celle-ci, elle ne se termine pas par des termes égaux à 0.
 

Fenêtre de Tukey

Pour cette fenêtre, le coefficient w est calculé ainsi :

ce qui donne une fenêtre :

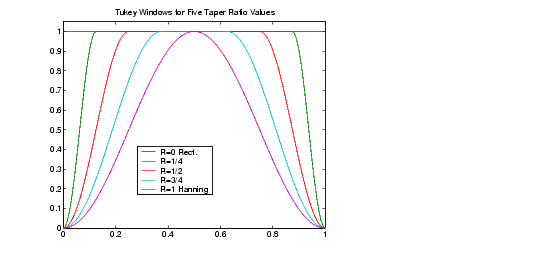
a est le rapport donnant la partie constante, défini entre 0 et 1. Si a est inférieur ou égal à 0, il s'agit d'une fenêtre rectangulaire ; s'il est supérieur ou égal à 1, d'une fenêtre de Hann.

Veuillez noter que le logiciel wavefft_z_.exe donnant WaveFFT.exe, emploie une autre formule, pour parvenir à la bonne fenêtre.

Aller à l'ensemble des fenêtres

Fenêtre de Hamming

Pour cette fenêtre, le coefficient w est calculé ainsi :

ce qui donne une fenêtre :
 

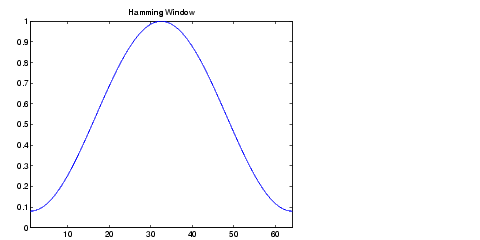
Elle est dérivée de la fenêtre de Hanning, mais ne s'annule pas sur les bords.

Fenêtre de von Hann, ou Hanning

La fenêtre de Hanning est favorable à la résolution de fréquence. Elle est employée pour l'étude des transitoires dont la durée est supérieure à la longueur de fenêtre ; pour l'analyse de systèmes par l'étude de réponses à des excitations aléatoires, ainsi que pour des usages généraux.
Pour cette fenêtre, le coefficient w est calculé ainsi :

ce qui donne une fenêtre :

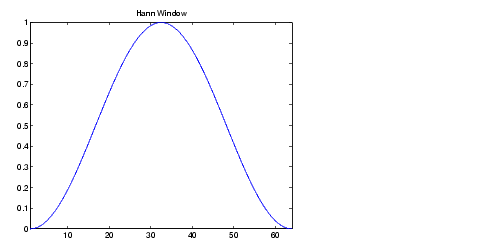
Aller à l'ensemble des fenêtres

Haut de la page

Fenêtre de Bartlett

Pour cette fenêtre, le coefficient w est calculé ainsi :

pour n impair :

pour n pair :

ce qui donne une fenêtre :

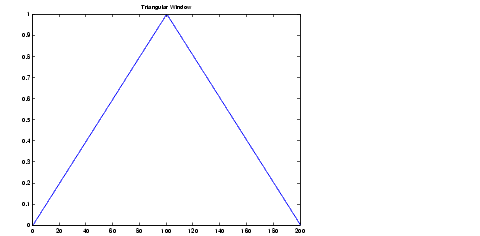
La fenêtre de Bartlett est très similaire à une fenêtre triangulaire ; par contre, elle se termine toujours par 0.
 

Fenêtre de Bartlett-Hann

Pour cette fenêtre, le coefficient w est calculé ainsi :

pour 
 

Fenêtre de Blackman-Harris

Pour cette fenêtre, le coefficient w est calculé ainsi :

avec : a₀ = 0,35875 ; a₁ = 0,48829 ; a₂ = 0,14128 ; a₃ = 0,01168.

ce qui donne une fenêtre :
 

Aller à l'ensemble des fenêtres

Fenêtre de Bohman

Pour cette fenêtre, le coefficient w est calculé ainsi :

où 

Cette fenêtre est une convolution de 2 lobes cosinusoïdaux de demi durée. Dans le domaine temporel, c'est le produit d'une fenêtre triangulaire et d'une fonction cosinusoïdale d'une seule période, avec addition d'un terme destiné à annuler la dérivée première aux bornes. Cette fenêtre décroît comme 1 / w⁴.

Fenêtre exponentielle

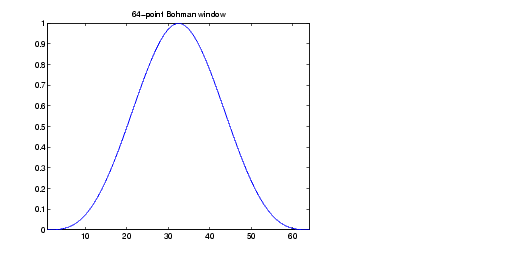
Pour cette fenêtre, le coefficient w est calculé ainsi :

w[k] = Exp ^{(k Ln(f) ) (n - 1))} avec k appartenant à l'intervalle [0, n - 1],

où f est la valeur finale de la fenêtre comprise entre 0 et 1.

Cette fenêtre est employée pour l'analyse des signaux transitoires dont la durée est supérieure à celle de la fenêtre. Elle peut être employée pour les signaux à décroissance exponentielle, comme les réponses de structures peu amorties excitées par un choc.

Aller à l'ensemble des fenêtres

Haut de la page

Fenêtre de Kaiser, ou Kaiser-Bessel

Cette fenêtre, ajustable, est employée pour la séparation de 2 sons de fréquences proches, mais d'amplitude très différente.
Pour cette fenêtre, le coefficient w est calculé ainsi :

Soit I₀ (x) la fonction de Bessel modifiée, d'ordre zéro.

I₀ (x) peut être approchée en retenant un nombre fini de termes dans la série infinie suivante :

I₀ (x) = 1 + S_i^µ₌₁  [(x / 2)ⁱ / i !]²

Supposons que nous souhaitions fixer l'atténuation relative du second lobe de diffraction, par rapport au lobe central, à la valeur A_SL, c'est à dire que dans une échelle logarithmique, où l'axe des ordonnées est gradué selon 20 Log |amplitude|, l'amplitude du premier lobe latéral soit inférieure de A_SL dB par rapport à celle du lobe principal.

Nous pouvons alors calculer un coefficient b de la manière suivante :

si A_SL < 13,26, alors b = 0 ;

si13,26 < A_SL < 60, alors b = 0,76609 (A_SL - 13,26)^0,4 + 0,09834 (A_SL - 13,26);

si A_SL > 60, alors b = 0,12438 (A_SL + 6,3) ;

et alors, avec a = (n - 1 ) / 2, pour k appartenant à l'intervalle [0, n - 1],

w[k] = I₀ [b (1 - [(k - a) / a]²)^1/2] / I₀ (b) et w[k] = 0 en dehors de cet intervalle.

Voici la fenêtre correspondant à un coefficient de 25 :

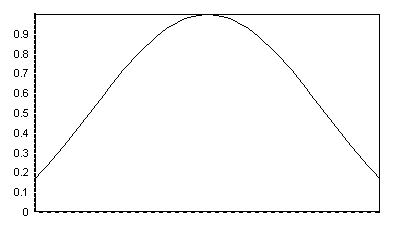
et voici celle correspondant à un coefficient de 250 :

Fenêtre de Chebyshev ou Tchebitchev, ou Dolph-Chebyshev

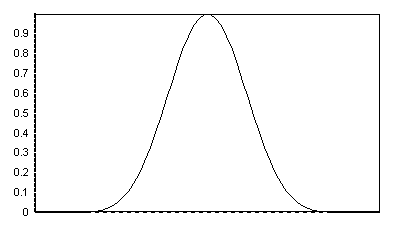
La transcription du nom étant phonétique, plusieurs orthographes sont possibles.

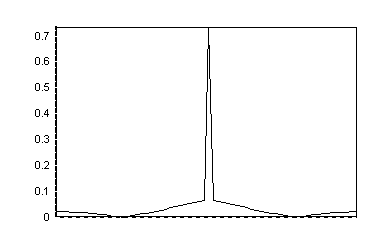
Pour cette fenêtre, le coefficient w est calculé ainsi :

w[k] = FFT^-1 [Cos(n Cos^-1[a Cos(p k / n)]) / CosH(n CosH^-1(a))],

où a = CosH ( CosH^-1(10) / n), avec

k appartenant à l'intervalle [0, n - 1].

Voici une telle fenêtre, tracée sur 64 points ; plus le nombre de points est élevé, plus le pic central est étroit.

Aller à l'ensemble des fenêtres

Influence de la fenêtre sur la résolution réelle en fréquence

Supposons que nous avons réalisé 1024 mesures, à une fréquence d'échantillonnage de 44100 Hz. La FFT sur 1024 points donne un spectre en fréquence qui s'étend de 0 à 44100 Hz. la deuxième moitié, symétrique de la première est sans intérêt. Le spectre utile s'étale donc de 0 à 22050 Hz. La résolution Df estimée en fréquence est donc de 44100 / 1024 ou 22050 / 512, soit 43 Hz entre deux points successifs du graphique. La durée T de mesure est de 1024 x 1 / 44100 = 0,023 seconde. Ces calculs montrent que Df = 1 / T.

Si nous sautons 1 point sur 2 dans le fichier, il faudra mesurer 2096 points, pendant donc 0,046 seconde. Le spectre complet en fréquence s'étendra de 0 à 22050, sur 1024 points ; Df vaudra 21,5 Hz.
 

Mais la résolution réelle en fréquence est toujours inférieure à la résolution ainsi calculée. Les fenêtres classées par ordre de résolution réelle décroissante sont :
Hamming, Hann, Blackman, Gauss 3.0, Kaiser-Bessel, FlatTop,

en excluant Rectangulaire et Bartlett, à cause de leurs défauts.
 

Exemples d'artefacts liés au type de fenêtre choisi

Fabriquons un signal artificiel en ajoutant 11 sinusoïdes de même amplitude, aux fréquences suivantes :

Observons le spectre de Fourier obtenu sans fenêtrage (fenêtre rectangulaire), en échelle logarithmique :
 

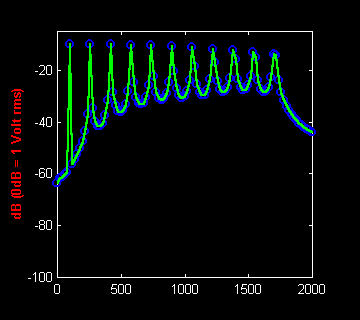
Le voici avec une fenêtre de Hanning :

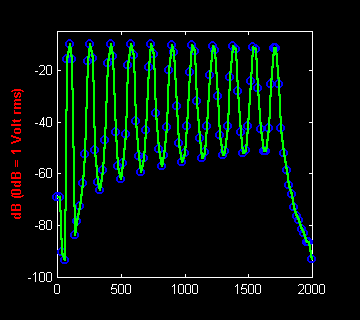
Et maintenant avec une fenêtre Flat Top.

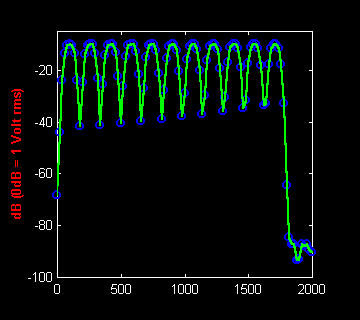
Le résultat est meilleur en ce qui concerne l'amplitude, mais les 'pics' sont étalés ; la résolution réelle en fréquence est moins bonne.

Aller à l'ensemble des fenêtres

Haut de la page

autres fenêtres :

Force, Saramaki-Rajan, Blackman exact, Poisson, Riez, Riemann, de La Vallé-Poussin, Hanning-Poisson,
Cauchy, Barcillon-Temes...