Il s’agit de mesurer un ordre de grandeur de la constante de gravitation
universelle, en moins d’une minute et dans les conditions d’une présentation
publique, avec un montage réalisable à l’aide de matériaux
et de matériel courants dans tout laboratoire de physique d’un lycée.
Ce mémoire, la description complète du montage avec ses
astuces de réglage et le code source, turbo Pascal pour Delphi 4
et 5, du logiciel pilotant l’expérience sont disponibles sur le
site http : // perso. wanadoo. fr / jussiaux. software /
Nous avons décidé de mesurer la constante de gravitation
universelle, par un montage inspiré de celui de Cavendish, mais
capable de donner un ordre de grandeur en moins d’une minute, grâce
à l’ajout d’un système d’asservissement piloté par
électronique, servant à la fois à mesurer un déplacement,
à stabiliser la partie mobile, et à diminuer la période
d’oscillation du pendule de torsion, puisque la durée de mesure
est proportionnelle à celle-ci.
Ce que nous n’avions pas mesuré, c’était la difficulté
de l’entreprise !
Malgré des dizaines de modifications destinées à optimiser le montage, nous verrons que, lors de l’approche des deux masses extérieures de 20 kg, les masses de plomb de 1,05 kg du pendule de torsion ne se déplacent que de 0,1 micron, valeur que nous devons mesurer dans les conditions d’une présentation publique, alors que le sol ne devrait pas s’incliner de plus de 2,5.10-7 radians, soit 0,05 seconde d’arc, soit encore ne pas s’enfoncer de plus de 1 micron.
Pour commencer, nous nous sommes inspirés du montage de Cavendish
commercialisé par la firme Leybold, qui est optimisé et donne
de bons résultats, mais nécessite deux heures de manipulation.
Ceci nous a entraînés sur une fausse piste. La méthode
classique nécessite pour être optimale que les masses mobiles
soient les plus faibles possibles, alors qu’il s’avère qu’ici au
contraire elles doivent avoir une valeur importante.
Ainsi, pendant des mois, nous avons mesuré des artefacts. L’heure
de la présentation publique approchant, nous avons suivi, sans grand
enthousiasme, les conseils de notre professeur : mettre au point une manipulation
plus classique, pour ne pas arriver les mains vides devant le jury. Mais
nous avons aussi décidé de modifier de fond en comble notre
montage de mesure de G, en augmentant très fortement la valeur des
masses mobiles, bien que persuadés que l’asservissement ne
parviendrait plus à jouer son rôle, ce qui fut le cas, nous
obligeant à modifier fondamentalement la partie mécanique,
pour faciliter la tache de l’asservissement.
Les nouvelles mesures nous ont semblé n’être que du bruit,
mais en rédigeant notre premier mémoire, l’idée nous
est venue de tracer dans Excel une droite de régression entre les
points de mesure. Mathématiquement, il s’agissait d’une erreur ;
malgré tout, à notre grande surprise, une légère
bosse nous est apparue sur la courbe tension fonction de la date, au bon
endroit, et de la hauteur attendue. Nous avons donc renouvelé les
expériences, amélioré encore le montage.
La présentation aux épreuves régionales a été un test de notre travail en temps réel : le jury ne disposait que d’un vague mémoire (et nous le prions à nouveau de bien vouloir nous en excuser), nous savions que l’asservisseur fonctionnait, puisqu’il était parvenu à stabiliser le pendule de torsion, alors qu’une entreprise était en train de casser au marteau piqueur la dalle de béton de la salle voisine ( ! ! ! ), mais nous ne savions pas quelle serait l’influence d’une assistance nombreuse : Le montage a fonctionné. Nous avons donc décidé de poursuivre nos mesures et améliorations, car nous pensons qu’il peut donner de meilleurs résultats encore. Ce compte rendu tient compte de nos observations expérimentales, et tel fait qui nous paraît relativement évident aujourd’hui ne l’était absolument pas au début de nos expériences.
Retour en haut de cette page
Nous envisageons de publier le descriptif complet du montage (taille
et matière du support, aimant, bobine, fil de torsion, astuces de
réglage ... ) sur un ou plusieurs sites Internet, ainsi que le code
source du logiciel d’exploitation des mesures. Consultez http ://perso.wanadoo.fr/jussiaux.software/
Nous avons choisi de construire notre montage avec des moyens courants,
dont dispose tout laboratoire de physique d’un lycée, sans avoir
recours à des pièces coûteuses ; le fil de torsion
est du fil de pêche, tenu par un noeud de pêcheur, l’outil
le plus sophistiqué est une perceuse sur support. Une réalisation
plus sophistiquée donnerait certainement des résultats plus
précis.
Figure 1 : (Voir aussi la figure 6 pour l’installation du système
d’asservissement).
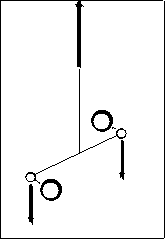Le
montage de Cavendish est, en apparence, très simple : L’action de
gravitation sur une masse m, de toute masse M d’encombrement et valeur
raisonnables étant négligeable devant l’action de la masse
terrestre, il suffit d’employer deux masses m qui s’équilibrent
sous l’effet de l’attraction terrestre, l’action d’une ou deux masses M
s’exerçant selon une direction horizontale, perpendiculaire à
l’effet de la Terre.
Le pendule de torsion ainsi constitué doit tourner d’un
(très petit) angle sous l’effet de M. Cet angle est mesuré
en comparant les deux positions moyennes autour desquelles le pendule de
torsion oscille, d’abord sans masse M, puis avec, car il est impossible
d’attendre que le pendule cesse d’osciller (temps très long, vibrations
parasites, déformation du fil de torsion, excitation provoquée
par l’approche des masses extérieures).
Le problème de cette manipulation est qu’elle est très
longue : L’oscillation du pendule de torsion a une période de l’ordre
de 10 minutes, dans le montage de la firme Leybold, et si on souhaite examiner
les caractéristiques d’une douzaine de périodes, 6 avant
de placer M, 6 après, il faut 2 heures pour une mesure de la constante
de gravitation.
Nous avons eu connaissance, par notre conseiller scientifique, Daniel
Van Labeke, professeur à l’Université de Besançon,
d’une réalisation d’un groupe de professeurs américains,
dont il était dit qu’elle fonctionnait, mais dont les données
essentielles n’étaient pas publiées. Qu’importe ! Il n’est
pas nécessaire de trop espérer pour entreprendre.
Nous décidons de doter le montage d’un système d’asservissement
électronique : La période T0 asservissement des oscillations
de torsion du pendule sera ramenée à une dizaine de secondes,
pour réduire le temps de manipulation : la mesure de la moyenne
de la tension de sortie de l’asservisseur sur une période avant
l’approche des masses M, puis sur la période suivante après
approche des masses M, nous donnera le déplacement des masses mobiles,
ce qui devrait nous permettre d’accéder en moins d’une minute à
la constante de gravitation. En effet, le théorème de superposition,
applicable ici, à partir du moment où toutes les relations
entre grandeurs sont linéaires (ce qui donc nécessite entre
autre que les amplificateurs intégrés linéaires ne
soient pas saturés) montre que si l’approche des masses extérieures
M se fait de manière quasi instantanée, à un instant
t, de t à t + T0 asservissement le pendule oscille autour
de sa nouvelle position moyenne. C’est ce que montre l’enregistrement figurant
sur le catalogue Leybold, et c’est ce que semblent montrer nos enregistrements
réalisés avec les dernières versions de notre circuit
électronique, dont la constante de temps a été réduite
à 1 seconde. Ces raisonnements supposent que l’amortissement du
système est faible. Nous avons donc, par tâtonnement, doté
l’asservisseur d’un faible amortissement, ce que confirment nos enregistrements
(figure 3).
Retour en haut de cette page
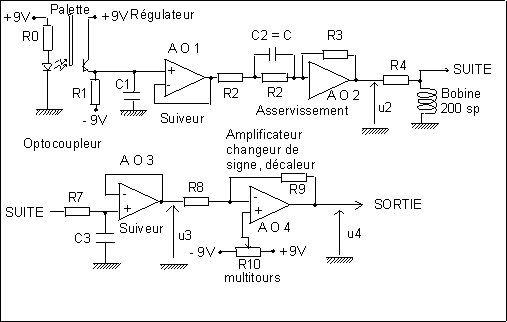
Par la suite W signifiera ohm, et m micro !
R0 = 2 200, puis 1 500 W, R1 = 147 kW, C1 = 10 nF, R2 =
100 kW, C2 = C = 2 mF, R3 = 1 MW, R7 = 10, puis 4,7, puis 1 MW, C3 = 1
mF, R8 = 10 kW, R9 = 100 kW, R10 = 47 kW, R4 = 470, puis 1470, puis 5 200
W.
Dans l’espoir de diminuer les parasites, nous avions employé des piles électriques pour réaliser l’alimentation + 9V, - 9V, mais la tension qu’elles délivrent varie au cours du temps provoquant une dérive des mesures ; nous avons donc installé des régulateurs + 9V et - 9V, alimentés pour l’instant en + 15V et - 15V.
Une palette (voir figure 6) fixée sur le bras mobile portant
les deux masses m, s’engage entre la photodiode et le phototransistor d’un
optocoupleur appelé aussi fourche optique. Son déplacement
provoque une variation de la quantité de lumière parvenant
au phototransistor, de l’intensité débitée par le
phototransistor dans la résistance R1 et donc de la tension appliquée
sur l’entrée non inverseuse de l’amplificateur n° 1 monté
en suiveur. Un condensateur C1 est destiné à éliminer
les parasites à haute fréquence. La valeur de R1 (147 kW)
est choisie pour que le mouvement complet de la palette (déplacement
de 1 mm), provoque une grande excursion de tension, entre - 9V et + 5V.
Cette tension est comparée à 0V.
Dans un premier temps, nous l’avions comparée à une valeur
positive, dans le but de n’employer que des tensions positives, pour simplifier
le montage, mais nous avons découvert que la comparaison à
0V diminuait de façon importante les parasites.
La capacité du condensateur C1 doit être la plus grande
possible, pour éliminer les parasites à haute fréquence,
mais sans aller jusqu'à une instabilité du montage d’asservissement.
25 nF rompent la stabilité, nous avons donc choisi 10 nF.
C’est le montage permettant l’asservissement. S’il ne comportait
pas le condensateur C2 ou C, la tension de sortie, donc l’intensité
dans la bobine de 200 spires serait proportionnelle (en fait, fonction
affine) au déplacement de la palette dans l’optocoupleur, du moins
lorsque la palette se trouve au milieu du faisceau infra rouge de 1 mm
de diamètre, partant de la diode électroluminescente vers
le phototransistor (zone où nous verrons que la réponse est
linéaire). Engagé partiellement dans la bobine, se trouve
un petit aimant droit, provenant d’une aiguille aimantée cassée,
fixé au bras mobile portant les deux masses m. Les déplacements
du bras mobile étant de très faible amplitude (beaucoup moins
que 1 mm, une fois le bras mobile sous contrôle de l’asservisseur,
de l’ordre de 8 microns, pour une variation de 5 V de la tension de sortie
du quatrième amplificateur ), la force électromagnétique
agissant sur l’aimant, toujours au même point dans la bobine, est
proportionnelle à l’intensité traversant la bobine, donc
au déplacement de la palette, autour de sa position d’équilibre.
Par contre, il n’est pas possible de calculer la valeur de cette force
pour une intensité connue, ce qui fait qu’il ne nous est pas possible
de déterminer à priori quelle intensité, et donc quelles
valeurs de résistances permettront d’atteindre la période
sous asservissement de 10 secondes que nous souhaitons. Cela complique
considérablement la recherche des valeurs optimales pour les montages
électrique et mécanique.
Notons que si le montage est déplacé, ou si le plancher
de la salle s’incline, cette valeur change, le bras mobile ayant tendance
à entrer ou sortir de l’asservisseur.
Il suffit de brancher la bobine dans le sens convenable, pour que cette
force devienne une force de rappel, provoquant une oscillation du bras
mobile, comme sous l’effet d’un « fil de torsion électronique
».
Mais cela ne suffit pas, car il faut aussi amortir le mouvement. Pour
cela, il faut créer une force proportionnelle à la vitesse
du bras, dérivée de sa position par rapport au temps, et
de sens opposé. C’est le rôle du condensateur C2 ou C. La
tension de sortie de l’AIL n° 2, u2, est égale à - R3.i,
où i est l’intensité traversant l’association de R2 et C
en parallèle. En appelant u1 la tension de sortie de l’AIL n°
1, i = u1/R2 + C du1/dt. La tension u2 est donc bien somme de termes proportionnels
au déplacement du centre de gravité de la masse m et à
sa vitesse, avec les mêmes signes.
A la date où ce rapport est rédigé, C vaut 2 mF.
Cette valeur produit des oscillations faiblement amorties (voir enregistrement
figure 3). Il faudrait l’augmenter pour accroître l’amortissement.
Mais si les oscillations sont pseudo sinusoïdales, peu amorties, le
calcul de la valeur moyenne de la tension sur une période donnera
un résultat proche de la tension moyenne que nous cherchons.
R4 est au début choisie égale à sa plus petite
valeur, 470 W ; en effet, la résistance de la bobine est négligeable
et ainsi, pour une tension de sortie de l’amplificateur 2 de 9 V, l’intensité
est de 20 mA, ce qui évite l’intervention du disjoncteur interne
à l’amplificateur, donc les non linéarités (ces valeurs
dépendent des amplificateurs choisis ; le TL 084 ne peut pas débiter
20 mA, mais 4 mA).
Le montage R7, C3 branché sur un montage suiveur permet d’obtenir
une valeur moyenne de la tension, c’est à dire le décalage
de la tension moyenne dû à l’approche des masses M, sans être
trop gêné par les oscillations de la tension dues aux oscillations
du bras mobile. En fait, pour que cela soit vrai, il faudrait que la constante
de temps R7 x C3 soit nettement supérieure à la période
d’oscillation de torsion qui vaut environ 10 secondes (les autres oscillations
parasites ont une période plus courte). Ce montage n’est pas un
intégrateur à amplificateur intégré linéaire,
dont nous savons qu’il provoque des dérives qui ici fausseraient
totalement les mesures.
Mais nous avons choisi une valeur beaucoup plus faible de la constante
de temps, pour accélérer la mesure. En ce cas, l’ensemble
R7 C3 se comporte comme un filtre passe-bas destiné à limiter
l’amplitude des oscillations, puisque c’est la valeur moyenne qui nous
intéresse. Dans un premier temps, nous avions choisi une constante
de temps de 10 secondes, nous sommes passés à 5 puis à
1 seconde.
Il s’agit d’un montage amplificateur changeur de signe, de gain
10, prévu au départ pour diminuer la valeur des masses M,
afin de rendre le montage facile à transporter, ce qui n’est plus
le cas aujourd’hui. Mais qui de toutes façons s’avère nécessaire
compte tenu de la faible sensibilité (2,5 mV) de notre vieux système
d’acquisition, à base de carte Candibus et surtout de sa sensibilité
aux parasites (50 mV crête à crête pour un signal de
0 V). Pour tenter de limiter les parasites, la tension u4 est aussi changée
de signe. La carte reçoit donc u4 sur son entrée 1 et - u4
sur l’entrée 2, le système de mesure calculant u4 -(-u4)
= 2 u4, gain 2. Cela s’avère assez efficace. De plus nous calculons
la moyenne d’un grand nombre de mesures (environ 157 000).
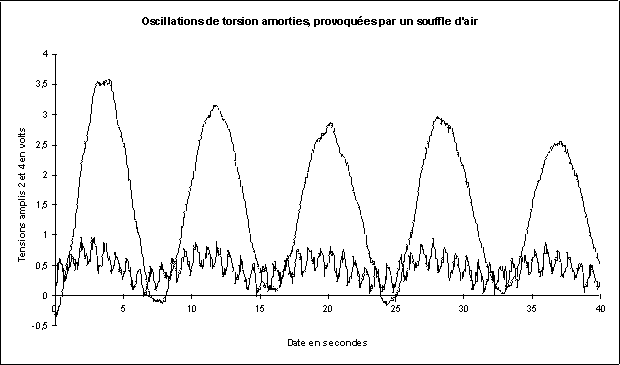
Le pendule de torsion est lancé par un léger souffle
d’air, créé à l’aide d’une soufflette de photographe
destinée à nettoyer les objectifs. La courbe du bas représente
la tension de sortie du deuxième amplificateur. On y observe les
oscillations du pendule de torsion, de période voisine de 8 secondes,
sur lesquelles se superposent les oscillations latérales de période
0,83 seconde.
La tension de sortie du quatrième amplificateur montre le gain
de 10 x obtenu pour la fréquence nulle et les basses fréquences,
et l’atténuation des oscillations plus rapides. Le montage est légèrement
amorti, comme souhaité. La constante de temps R7 C3 vaut ici 1 seconde.
Figure 3
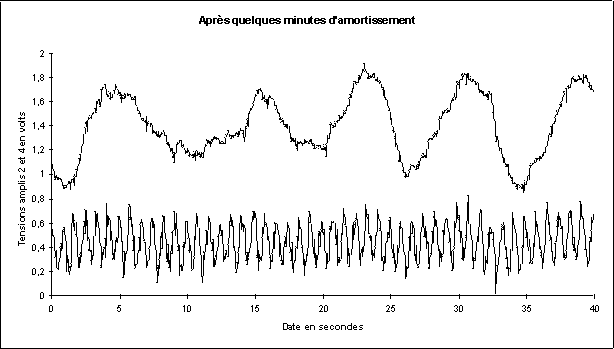
Même enregistrement, quelques minutes plus tard : Les oscillations latérales sont toujours là, les oscillations de torsion sont plus faibles, mais fortement perturbées, sans doute par des vibrations parasites.
Figure 4
Etude des dérives de la tension de sortie de l’amplificateur
n° 4, avec son changeur de signe, sur une longue durée.
Chaque point correspond à la valeur moyenne obtenue en effectuant
15 700 mesures par seconde pendant 40 secondes. L’axe des ordonnées
correspond à une variation de 3,5 V. Figure 5
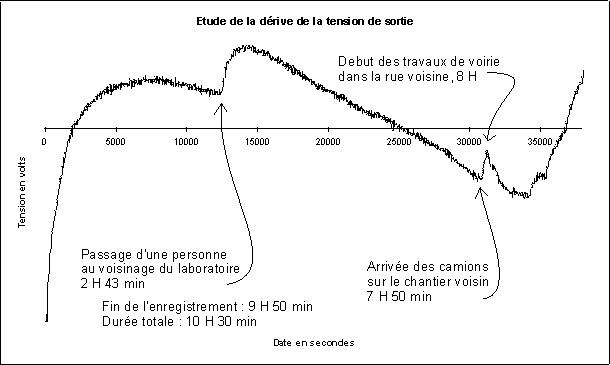
La dérive est essentiellement due à une déformation
progressive du fil de torsion (fil de pêche en Nylon). Elle est beaucoup
moins rapide ici (3,5 V en 10 heures) que sur la figure 8 (2 V en 5 minutes),
parce que le fil est sous tension depuis plusieurs jours.
Retour en haut de cette page
Nous décidons de commencer avec des masses voisines de celles
utilisées par Leybold, voire un peu plus faibles, car nous faisons
preuve d’une foi qui s’avérera excessive dans les vertus de l’électronique,
et pourquoi ne pas employer les masses marquées en laiton disponibles
au laboratoire ?
Nous commençons avec deux masses m = 50 g et une masse
M = 800 g.
Figure 6:
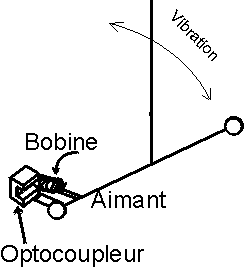Mais pendant plusieurs
mois et malgré plusieurs dizaines de modifications de notre montage,
nous ne parvenons pas à observer quelque chose de crédible.
Au début, la tension de sortie du montage électronique
présentait une allure curieuse, hachée, et parfois, le montage
émettait un sifflement. Les oscillations avaient une fréquence
de 14, ou 1 000 Hz. Nous avons fini par découvrir que le bras mobile
oscillait de manière tout à fait imprévue, selon le
schéma ci contre.
Un spécialiste en asservissements, Monsieur Fischer, du lycée
Jules Haag, nous apporte l’information suivante : ‘Souvent, dans les systèmes
asservis, les problèmes proviennent de la partie mécanique’.
Nous modifions le montage mécanique et le schéma électronique
de départ (la figure 2 donne le montage actuel).
Figure 7 :
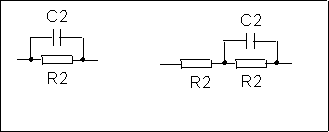Le
premier montage était celui de gauche sur la figure ci contre ;
il donne bien le résultat attendu, intensité de sortie de
l’amplificateur 2 somme d’un terme proportionnel au déplacement
de la palette liée au bras mobile et d’un terme proportionnel à
la vitesse de la palette, avec des coefficients de même signe, qui
sont rendus négatifs en choisissant le sens de branchement de la
bobine. Par contre, l’impédance du condensateur tendant vers 0 en
haute fréquence, celles-ci sont fortement amplifiées, ce
qui n’est pas bon. Le montage de droite est bien meilleur : il donne bien
la forme d’intensité attendue, le gain en basses fréquences
est deux fois plus faible en valeur absolue(R3/2R2 au lieu de R3/R2), mais
le gain en hautes fréquences est limité à deux fois
le gain en basses fréquences, au lieu de tendre vers l’infini (R3/R2,
puisque C2 court-circuite la deuxième résistance R2).
La vibration à 1 000 Hz disparaît, mais pas celle à
14 Hz.
Nous décidons donc de refaire toute l’installation mécanique,
pour empêcher cette vibration : nous ajoutons une grosse masse, puis
un deuxième fil tendu, au dessous du bras mobile.
Et puis un jour, nous obtenons la variation tant attendue de la tension
de sortie, à l’approche d’une masse extérieure.
Hélas, nous ne parvenons pas à reproduire le phénomène.
Mais Bruno a remarqué qu’au moment où le montage a semblé
fonctionner, les parasites électriques avaient disparu.
Nous entreprenons la chasse aux parasites, remplaçant notre
alimentation électronique par un jeu de piles électriques,
allant même jusqu'à blinder totalement le montage, ce qui
n’est guère pratique, car les réglages deviennent très
pénibles, étant donné qu’on ne peut plus voir si la
palette fixée au bras mobile s’engage correctement dans l’optocoupleur,
ou si elle vient frotter ou butter contre celui ci.
Cela ne suffit pas.
Nous constatons d’autres effets indésirables : vibrations du
plancher de notre salle de travail, influence de la lumière extérieure.
Nous fermons la boîte contenant le bras mobile.
Nous trouvons un local en sous-sol, moins sujet aux vibrations, mais
qui ne peut nous être attribué qu’une fois chaque semaine.
Le pendule de torsion sorti d’un placard demande au moins quinze minutes
pour être pris sous le contrôle de l’asservissement, temps
que nous employons à descendre notre ordinateur de mesure depuis
le laboratoire de physique.
Un jour enfin, la tension de sortie réagit de façon répétitive.
Mais pas du tout avec la même valeur absolue, selon que la masse
extérieure M (masse marquée en laiton de 1 kilogramme) est
approchée d’un côté ou de l’autre ; en fait beaucoup
trop d’un côté et pas du tout de l’autre.
Nous finissons par trouver l’explication : les masses marquées
en laiton sont lestées et doivent contenir un matériau magnétique
qui réagit avec l’aimant de l’asservissement. Un bloc de plomb de
même masse ne produit aucun effet mesurable.
Et puis la tension de sortie dérive rapidement ; le mauvais
réglage du potentiomètre ajustable multitours en est l’une
des causes : il est en butée et sa résistance varie très
vite et pas dans le sens prévu, mais ce n’est pas la seule cause.
Un jour, nous observons même une belle oscillation sinusoïdale
de période 10 secondes, comme nous l’espérions, mais elle
ne se reproduit plus jamais :
Retour en haut de cette page
La date de la présentation de notre travail approchant de
manière inéluctable, nous tenons un conseil :
Le professeur nous incite à changer de sujet, quitte à
terminer celui-ci l’année prochaine. Nous préférons
nettement poursuivre. Nous prenons les décisions suivantes :
Premièrement, nous lançons un deuxième sujet que
nous sommes certains de maîtriser, il s’agit d’une manipulation de
pHmétrie.
Deuxièmement, nous modifions totalement le montage de mesure
de la constante de gravitation, dans l’espoir de le rendre plus sensible,
mais en craignant que l’asservissement ne parvienne plus à prendre
le contrôle du bras mobile. Pour cela, nous augmentons fortement
les valeurs des masses employées, ce qui nous fait nous écarter
en partie de notre objectif d’un montage facilement transportable. Les
masses mobiles deviennent 21 fois plus importantes (1 050 g), la masse
extérieure est remplacée par deux masses plus grosses (20
kilogrammes chacune, gain de 50 fois) et l’électronique est modifiée
(La résistance R4 passe de 470 à 1 470 , soit un gain de
3 fois), pour que l’asservissement soit moins « raide ». Nous
trouvons du plomb de récupération et le chalumeau pour le
fondre chez un artisan plombier qui met bien du temps à retrouver
sa louche à fondre le plomb, car les soudures au plomb se font heureusement
rares. Les masses M sont formées par deux demi sphères (»)
coulées dans la louche du plombier remplie à ras bord, les
masses m sont coulées dans un moule en plâtre où des
lampes d’éclairage sphériques ont laissé leur empreinte.
Mais cela impose de refaire la partie mécanique du montage,
car les masses m sont beaucoup plus grosses. Le fil de Nylon de diamètre
12/100 de mm est remplacé par du 35/100.
Nous constatons alors que lorsque les masses m sont suspendues, le
fil de Nylon s’allonge fortement (environ 2 cm et ce n’est pas nouveau),
mais aussi qu’il a tendance à se vriller de plusieurs tours. Le
système d’asservissement qui a 63 fois (m x 21 et R4 x 3) plus de
mal à prendre le contrôle du bras mobile n’y parvient plus
et c’était là notre crainte. Nous devons ajouter un système
en haut du boîtier, permettant de compenser le vrillage du fil de
suspension.
Lorsqu’enfin le bras est sous contrôle, nous observons une dérive
rapide et inéluctable de la tension de sortie. Elle persiste après
que le potentiomètre soit mieux réglé. Cette dérive
ralentit beaucoup si le montage reste plusieurs jours en service (20 fois
moins vite, au bout d’une semaine), sans être déplacé.
Il arrive qu’elle change de sens entre deux séances de mesure :
le fil de Nylon doit se déformer en permanence. Nous renforçons
la rigidité du boîtier supportant le montage. Nous recherchons
un autre matériau pour le fil. Un prothésiste dentaire nous
propose du fil d’argent (il nous semble que c’était l’un des matériaux
employés par Cavendish) et réalise lui-même un test
: le fil de 0,1 mm de diamètre casse sous une charge de 2 kilogrammes
; et il ne dispose par ailleurs que d’un fil de 0,5 mm de diamètre.
Il dispose aussi de fil de bronze (le montage Leybold emploie un ruban
de bronze), mais de trop gros diamètre. Depuis, nous en avons trouvé
d’autres.
Dans un premier temps, nous décidons de garder le fil Nylon,
et de le laisser s’allonger aussi longtemps que possible, ce qui n’est
pas simple puisque nous devons libérer notre local en sous-sol à
chaque fois et qu’il nous faudra transporter notre montage jusqu’au lieu
du concours.
En transférant les résultats de mesure dans Excel, il
semble malgré tout possible de les exploiter.
Retour en haut de cette page
La courbe suivante,
figure 9, est notre premier enregistrement qui peut-être contient
quelque chose de significatif : C’était le seul disponible lors
de la rédaction du mémoire pour le concours régional,
et à vrai dire, c’est en rédigeant ce mémoire que
nous avons découvert sur la courbe une petite bosse intéressante.
Cette bosse est mesurée par rapport à la droite obtenue par
régression linéaire sur tous les points de mesure ; il s’agit
d’une erreur mathématique, mais elle nous a permis de déceler
(peut être) un phénomène physique intéressant.
La méthode expérimentale employée est la suivante
:
A l’oscilloscope, nous suivons la tension de sortie de l ‘amplificateur
n° 2, alimentant la bobine ; nous réglons la torsion du fil
de Nylon pour que la palette fixée au bras mobile portant les deux
masses m vienne se placer au milieu du faisceau lumineux de l’optocoupleur.
Après une phase d’oscillations de trop grande amplitude (quelques
millimètres) pendant laquelle la tension évolue en créneaux
et qui dure environ un quart d’heure, l’asservissement prend le contrôle
du pendule de torsion. Nous voyons des oscillations amorties de pseudo
période voisine de 10 secondes, auxquelles se superposent des oscillations
de période 1,28 seconde qui se révèlent correspondre
à un balancement latéral du pendule, balancement qui n’est
pas amorti par l’asservissement, quoique la forme de l’extrémité
de la palette entrant dans l’optocoupleur ait de l’importance, provoquant
un couplage entre ces deux oscillations.
Nous effectuons 15 700 mesures par seconde, pendant une période
complète d’oscillation de torsion (10,3 s cette fois ci) et en calculons
la moyenne.
Nous observons sur notre enregistrement, figure 9,de la tension moyenne
de sortie de l’amplificateur n° 4 :
§ une rapide dérive, de 2V en 4 min 30 s (le fil
n’est pas sous tension depuis longtemps), qui nous oblige à retoucher
souvent le réglage du potentiomètre ajustable multitours
R10, ce qui à chaque fois perturbe le montage pendant plusieurs
minutes,
§ des fluctuations importantes dont nous ignorons pour l’instant
la cause (sans doute des vibrations parasites) et un décalage d’environ
2 mm soit 51 mV (à ± 25 mV ! ) qui correspond à l’approche
d’une seule masse M extérieure de 20 kg, à environ 15 cm
de m, de centre de gravité à centre de gravité, avec
un décalage dans le temps d’environ 20 secondes, ce qui peut s’expliquer
par la présence du filtre R7 C3 dont la constante de temps est,
pour cette première mesure, de 10 secondes. Nous n’avons approché
qu’une seule masse M par commodité, mais l’idée est mauvaise,
car elle rompt la symétrie du montage et produit aussi une translation
du bras mobile.
Figure 9 :
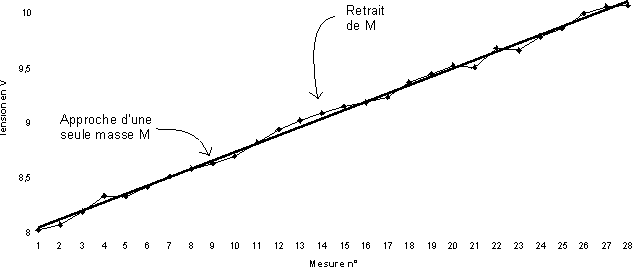
Approche d’une masse M extérieure au point 9, retrait au point
14. Une mesure de tension moyenne sur une période (10,3 s) de sortie
de l’amplificateur n° 4, toutes les 10,3 + 0,5 seconde (les 0,5 s sont
destinées à l’affichage des résultats). Constante
de temps R7 C3, 10 secondes, pas d’amplificateur changeur de signe, pour
cette première mesure.
Retour en haut de cette page
Pour mesurer la tension de sortie, le plus simple serait d’employer
un voltmètre sur un calibre continu. Mais alors, il faut que le
montage électronique fasse la moyenne de cette tension de sortie
sur une durée très supérieure à la période
d’oscillation sous asservissement, qui est de 10 secondes environ.
Il nous a semblé qu’une autre technique serait plus rapide :
faire un grand nombre de mesures durant une période entière
exactement, et en faire la moyenne mathématiquement.
Pour cela, nous avons mobilisé nos connaissances acquises en
option informatique de classe de terminale et en IESP.
Notre professeur avait rédigé l’année dernière
une bibliothèque Delphi, destinée à piloter les cartes
d’acquisition Candibus (elle est disponible sur son site, http :
// perso.wanadoo.fr / jussiaux.software /).
Dès lors, la rédaction de notre programme a été
très rapide, puisque nous disposions des fonctions et procédures
toutes prêtes d’acquisition d’une série de mesures, d’acquisition
d’une valeur moyenne, de transfert dans Excel ...
Le logiciel effectue 15 700 mesures par seconde (il ne peut pas travailler
à n’importe quelle fréquence) sur une durée réglable
autour de 10 secondes, effectue u(entrée 1) - u(entrée 2),
en donne la moyenne, trace le graphe des mesures successives et transfère
le tout dans Excel. Il calcule aussi, par régression linéaire
(les formules de calcul ont été trouvées dans le mode
d’emploi d’une calculatrice Casio) la droite moyenne selon laquelle dérive
la tension (en utilisant les premiers et derniers groupes de points mesurés
en l’absence des masses M), le décalage par rapport à cette
droite de la tension moyenne obtenue lorsqu’on approche les masses M d’un
côté puis de l’autre, et en déduit la valeur de la
constante de gravitation universelle mesurée.
Lorsqu’une mesure est en cours, par contre, l’usage de la souris est
impossible.
Le code source est disponible sur http : // perso.wanadoo.fr
/ jussiaux.software /.
Retour en haut de cette page
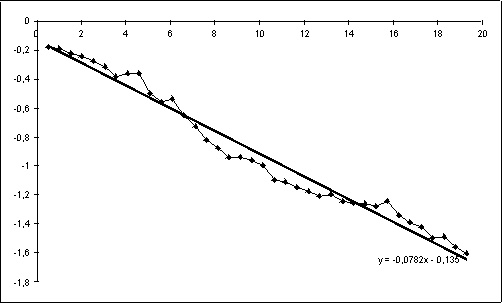
Aujourd’hui, la dérive a changé de sens. La constante
de temps R7 C3 a été ramenée à 5 secondes.
Nous avons approché les deux masses M d’abord d’un côté,
posées sur deux planches à dessin reposant sur des piles
de livres, mais pas assez près car Bruno, ayant très peur
de l’intoxication au plomb, avait entouré sa boule dans du papier
qui risquait de toucher le bâti du montage. Puis de l’autre, enfin,
comme la première fois. Il semble que quelque chose de cohérent
se passe, le montage réagit très vite, et dans le sens attendu,
à l’approche des boules et de ceux qui les portent, mais nous sommes
devenus méfiants ; il s’agit peut-être d’un déplacement
d’air, ou d’un basculement du sol, lors du déplacement des masses.
Il faudrait un support rotatif pour les deux boules M, comme dans le montage
de Cavendish, mais l’acier nous est interdit.
Nous réalisons un support en bois qui éclate au premier
essai.
Nous découvrons un bogue dans notre programme : les temps sur
l’axe des abscisses sont fantaisistes.
Deuxième mesure :
Bruno et Jean-Philippe sont décidés à approcher
les masses M au plus près (0,5 à 1 cm du bâti).
Figure 11 :
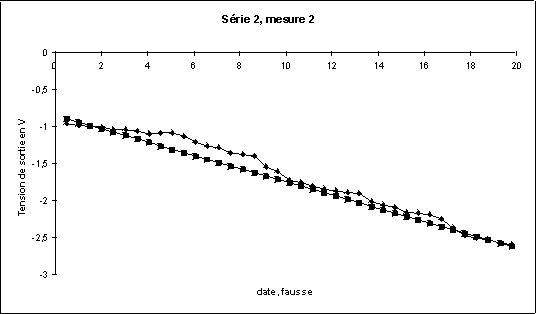
Masses M éloignées, puis d’un côté à
13,8 cm de centre de gravité à centre de gravité,
puis de l’autre à 13,8 cm, puis de l’autre à 13,8 cm, puis
éloignées. La droite de régression est calculée
à partir des points obtenus lorsque les deux masses M étaient
éloignées.
Troisième mesure, figure 12 :
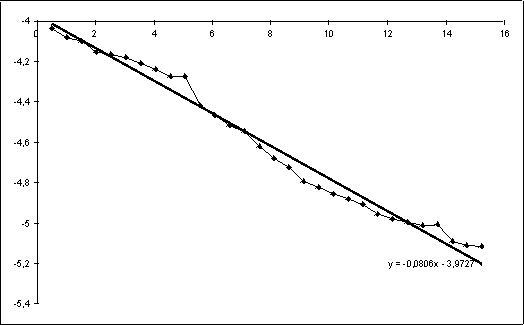
Masses M éloignées, puis d’un côté
à 13,8 cm, puis de l’autre à 13,8 cm, puis de l’autre et
... La courbe se déforme : Les dérives ont amené la
carte Candibus à sa tension minimale admissible ... et la séance
est terminée, nous devons ranger tout le matériel ... Il
semble cependant que les masses M ne soient pas bien alignées avec
les masses m, et le boîtier étant fermé à cause
des courants d’air et de la lumière parasite, cela est difficile
à vérifier.
Retour en haut de cette page
Comme il a été dit plus haut, il n’est pas possible
de mesurer directement la force (très faible) exercée sur
le petit aimant par la bobine de 200 spires, parcourue par une intensité
connue. On pourrait envisager un montage délicat, où les
intensités seraient augmentées dans un rapport important
(1 000 fois plus), puisque la force est proportionnelle à l’intensité,
mais le résultat ne serait valable que pour une seule position relative
de l’aimant et de la bobine.
Donc les mesures de valeurs de forces ou de la constante de gravitation
seront indirectes.
De plus, nous avons remarqué que d’une séance à
l’autre, la période du bras mobile portant les masses m, lorsqu’il
est sous contrôle de l’asservissement, varie de façon assez
importante : 10,3 s la première fois, 8,63 puis 9,8 puis 9,35
s la dernière fois. La variation se produit même au cours
d’un amortissement : 9,8 puis 9,35 s une minute et demi après.
En fait, c’est celle-ci qui nous intéresse, mais elle n’est
pas mesurable directement ici, car trop faible.
L’approche des deux masses M extérieures crée un couple
de forces sur le bras mobile qui tourne d’un angle a, mesuré généralement
par des moyens optiques, ou à l’aide de cellules photoélectriques,
comme dans le montage proposé par la firme Leybold.
La connaissance de C et a permet de calculer la valeur du couple de
forces, d’en déduire la valeur d’une force, et connaissant les distances
entre centres de gravité, d’en tirer la valeur de la constante de
gravitation universelle.
La méthode est directe, mais demande 2 heures pour une mesure.
Le début de la manipulation est le même, calcul de
J, mesure de T0, ici avec du fil de pêche de 35/100 mm, d’environ
2 min 17 s, à ± 10 s (le résultat pourrait être
plus précis, mais les débattements des masses m dans leur
boîtier est de très faible amplitude. Si on les sort, il y
a risque de changer la longueur du fil en Nylon, de plus la partie inférieure
du fil intervient aussi dans la valeur de T0). Nous obtenons la constante
de torsion C du fil.
Nous mettons en service l’asservissement et notons la valeur moyenne
de la tension de sortie de l’amplificateur n° 2. Nous tournons le support
supérieur du fil d’un angle a et mesurons la nouvelle valeur moyenne
de cette tension. De C et a, nous déduisons la valeur de la
force supplémentaire créée par l’asservissement, correspondant
à la variation des tensions moyennes mesurées.
Toute variation de tension moyenne de sortie de l’amplificateur n°
2, ou du n° 4, permettra de calculer la valeur de force correspondante.
A cette occasion, il nous est apparu un défaut de réalisation
de notre montage : le support du fil Nylon n’étant pas centré
correctement, une rotation produit aussi un déplacement de la palette
dans l’optocoupleur. Les résultats obtenus ne sont donc qu’indicatifs.
Application numérique :
Calcul du moment d’inertie J du bras mobile portant les deux masses
m, par rapport à un axe D passant par le fil de suspension :
Moment d’inertie d’une sphère de plomb de diamètre 6,2
cm et de masse 1 050 g par rapport à un axe passant par son centre
de gravité :
J1 = 2/5 (1,05 . (0,062/2)2, donc J1 = 4,04 .10-4 kg.m2,
moment d’inertie d’une masse ponctuelle de 1 050 g, placée au
centre de gravité d’une masse m, par rapport à l’axe de rotation
(distance D, centre de gravité de m = 8,3 cm) :
J2 = m.R2, ou J2 = 1,05.0,0832, donc J2 = 7,23.10-3 kg.m2
J = 2.(J1 + J2), d’où J = 0,0153 kg.m2.
De la relation T0 = 2 Pi (J / C)1/2, nous tirons C
= J (2 Pi /T0)2 , avec T0 = 137 s,
donc C = 0,0153.(2.pi/137)2, ou C = 3,21 . 10-5
N.m.rad-1,
pour du fil de pêche de 35/100 de mm, long d’une trentaine de centimètres.
A titre de comparaison, le ruban de torsion Leybold a une constante
de torsion de 8,5 . 10-9 Nm.rad-1, soit 4 000 fois
moins pour des masses 70 fois plus légères (en supposant
que leur fil a la même résistance par unité de section
que le nôtre, il est 4 0002/3 = 250 fois moins solide)
; le montage Leybold est 60 fois plus sensible que le nôtre, ce qui
est obtenu par la diminution des masses m, mais notre objectif est différent.
Tournons le support supérieur d’un angle a, en déplaçant
l’extrémité d’un rayon de 70 mm, de 3 mm. (Il aurait fallu
aussi tourner la partie inférieure du fil, ce que ne permet pas
notre montage).
a vaut 3/70 = 0,0429 rad , et la palette et le bras mobile ne bougent
quasiment pas.
La tension moyenne de sortie de l’amplificateur n°2 varie de 1,9
V ; celle du quatrième amplificateur de 1,9 x 10 = 19 V. Des mesures
ultérieures ont montré que cette valeur peut fluctuer beaucoup,
à cause d’un mauvais centrage du fil de suspension en Nylon.
Cette variation de 19 V correspond à une variation du couple
appliqué par le fil de torsion au bras mobile de M = C.a, ou M =
3,21 . 10-5 x 0,0429 = 1,38 . 10-6 N.m.
Lors de la première expérience semblant significative,
lors de l’approche d’une seule masse extérieure M, nous décelons
un décalage de la courbe de 2 mm, par rapport à la droite
moyenne, soit une variation de tension moyenne de 51 mV (avec une énorme
incertitude relative). Notons que ces 51 mV sont voisins du bruit de la
carte d’acquisition Candibus employée.
Le couple créé par l’approche d’une seule masse M de
20 kg, à 15 cm d’une des deux masses m (de centre de gravité
à centre de gravité) est d’environ :
1,38 . 10-6 x 0,051 /19, soit 3,70 . 10-9
N.m.
La force détectée vaut donc 3,70.10-9/0,083,
soit 4,46.10-8 N (le poids d’une gouttelette d’eau de 1/10 de
mm de rayon).
Mais le problème est plus compliqué, car la masse
M attire chacune des deux masses m. Figures 13 et 14.
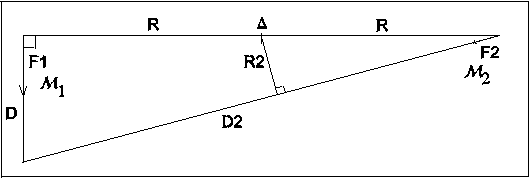
La force mesurée vaut donc 4,46.10-8 /0,70 =6,37.10-8
N, avec une très grande incertitude relative.
Pour voir si nous sommes enfin « dans le vrai », calculons
cette force, selon la loi de Newton :
F = 6,67.10-11 . (20 x 1,05)/0,152 , soit F = 6,2.10-8
N.
Nous ne nous faisons pas d’illusions sur la précision de nos
mesures, mais nous savons maintenant que nous sommes dans le bon ordre
de grandeur, ou encore, nous avons mesuré une constante de gravitation
de
7.10-11 Nm2kg.
Elle consiste à calculer le moment d’inertie J du bras mobile,
comme précédemment.
La mesure de la période d’oscillation du bras, lorsque celui-ci
est sous le contrôle de l’asservisseur, permet de trouver une constante
Casservissement analogue à une constante de torsion C.
Une variation de la tension de sortie moyenne de l’amplificateur n°
4 correspond à un déplacement de la palette dans l’optocoupleur
; ce déplacement correspond à une rotation d’un angle a du
bras mobile, qui nous permet, connaissant Casservissement, de déduire
le moment du couple de forces d’asservissement, lui-même égal
en valeur absolue au couple des forces de gravitation appliqué aux
masses m ; donc nous pouvons trouver la valeur des forces de gravitation.
Pour cela, il nous faut mesurer la variation de la tension de sortie
de l’amplificateur n° 4, lorsque la palette avance d’une certaine distance
dans le faisceau lumineux.
J a été déjà calculé plus haut
; J = 0,0153 kg.m2.
T0 asservissement = 10,3 s, pour cette mesure là.
Donc Casservissement = 0,0153.(2.pi/10,3)2 = 5,68.10-3
N.m.rad-1.
Dans cette valeur, bien plus grande qu’auparavant, la constante de
torsion du fil de Nylon intervient pour moins de 0,6%.
Evaluons la variation de la tension de sortie de l’amplificateur n°
4, lorsque la palette avance d’une certaine distance dans le faisceau lumineux.
Une première estimation rapide peut être faite : le faisceau
a un diamètre de 1 mm environ et selon qu’il est coupé ou
pas, la tension aux bornes de la résistance R1, en sortie du phototransistor
passe de -9V à + 5V. Le gain de l’amplificateur n° 1 est de
1, celui de l’amplificateur n° 2 est de 5, pour les très basses
fréquences et le continu (fréquences nettement inférieures
à 1 / (2piR2C2) » 0,8 Hz), celui du n° 3 est de 1 et celui
du n° 4 est de 10 (sans compter le gain de 2 dû au changeur de
signe installé dès la deuxième mesure). Donc la tension
de sortie varie de 14 x 5 x 10, soit 700 V pour un déplacement de
1 mm du bras mobile, au niveau de la palette, ou 7 . 105 V.m-1.
Une mesure plus soignée a été réalisée,
avec le premier montage (il nous faudra la refaire avec le montage actuel),
où la palette était très proche du centre de gravité
d’une masse m : Elle a consisté à ouvrir le boîtier,
à tordre fortement le fil Nylon, pour que la palette ait tendance
à sortir de l’optocoupleur, et à repousser celle-ci, à
l’aide d’un palmer.
Voici le tableau des résultats obtenus. Notons tout de suite
que ceux-ci ont pu varier, suite aux démontages et remontages de
l’optocoupleur et au changement de position de la palette sur le bras mobile.
| Lecture palmer 1/100 mm | 50 | 10 | 0 | 90 | 80 | 70 | 60 | 50 |
| tension AO1 en V | 3,55 | 3,64 | 3,69 | 3,73 | 3,68 | 3,68 | 3,66 | 3,47 |
| 1/100 mm | 40 | 30 | 20 | 10 | 0 | 90 | 80 | 70 |
| V | 3,32 | 3,12 | 2,85 | 2,41 | 1,75 | 0,32 | -1,13 | -2,57 |
| 1/100 mm | 60 | 50 | 40 | 30 | 20 | 10 | 0 | 90 |
| V | -3,88 | -5,03 | -6,19 | -7,04 | -7,04 | -7,65 | -7,66 | -7,66 |
Représentons tous les points de mesure, figure 15 :
Voici la zone où la relation est linéaire ; elle correspond à un déplacement de 0,7 mm, pour une variation de tension de 9 V. Figure 16.
Rappelons qu’il s’agit de la tension aux bornes de la résistance
R1, en sortie du phototransistor, et donc en entrée de l’amplificateur
suiveur n° 1.
La régression linéaire nous indique que la variation
de la tension en volts vaut 0,1275 fois le déplacement en 1/100
de mm de la palette, ou ici du centre de gravité d’une masse m,
soit 12 750 V.m-1, à multiplier par les gains successifs,
1x, 5x, 1x et 10x (ainsi que 2x, si le changeur de signe est en service),
soit finalement 6,38.105 V.m-1, assez proches de la première
estimation. Compte tenu du gain de 5x de l’amplificateur n° 2, nous
savons maintenant que lorsque cet amplificateur n’est pas saturé,
donc donne en sortie entre -9V et +9V, la palette liée au bras mobile
est dans une zone de l’optocoupleur délivrant entre - 1,8V et +
1,8V, où la réponse est linéaire. En examinant le
graphique précédent de plus près, nous voyons que
la pente de la droite passant au plus près de ces points est plus
forte ; Excel nous donne son équation : y = 0,144 1 x - 12,66. La
sensibilité est donc plutôt de 14 410 V.m-1 en
sortie du phototransistor et de 7,2.105 V.m-1 en sortie de l’amplificateur
n° 4. Nous reprendrons ces mesures, avec le montage « définitif
».
Nous avons constaté, lors de la première mesure ayant
peut-être un sens, une variation de la tension moyenne de sortie
de l’amplificateur n° 4 de 51 mV, lors de l’approche d’une masse extérieure
M de 20 kg, à 15 cm de la masse m de 1,05 kg. Cela correspond à
un déplacement de la position moyenne de la palette de :
51.10-3 / 7,2.105 = 7,08.10-8 m ou
71 nm (trente cinq fois la longueur d’une molécule d’huile). Nous
étions tout à fait fondés à négliger
le déplacement de la palette, dans les raisonnements précédents.
Ce déplacement correspond à un angle de torsion a’ (alpha
prime) de 7,08.10-8 / 0,083 (où 0,083 est le rayon de
rotation), mais nous supposons ici que la palette est à la même
distance de l’axe de rotation D que le centre de gravité de la masse
m, ce qui n’est plus vrai, car pour des raisons d’encombrement des masses
m, elle est maintenant plus loin, 11 cm ; il faudrait faire a’ = 7,08.10-8
/ 0,11, soit a’ = 6,44.10-7 rad.
Compte tenu de la « constante de torsion » équivalente
à l’asservissement, cet angle a’ correspond à un couple créé
par l’asservissement de Casservissement * a’, soit
5,68.10-3 x 6,44.10-7 = 3,66.10-9
N.m, soit encore à une force unique de
3,66.10-9 / 0,083 = 4,41.10-8 N mesurée.
En reprenant le raisonnement précédent sur l’interaction
entre la masse M extérieure et les deux masses m, la force d’interaction
gravitationnelle entre m et M vaut environ :
4,41.10-8 / 0,70 ou 6,30 .10-8 N.
Pour une force d’interaction gravitationnelle qui doit être
de 6,2.10-8 N, la méthode 2 a donné une mesure
de 6,4.10-8 et la méthode 3 de 6,3.10-8 N,
mais avec des incertitudes relatives énormes.
N’oublions pas que ces résultats sont d’une part indirects et
que donc chaque mesure intermédiaire est source d’erreurs, et que
d’autre part, la variation de tension moyenne observée correspond
à un décalage de 2 mm sur une courbe très perturbée.
Ramenés à la mesure de la constante de gravitation universelle,
nos raisonnements donnent :
G = 7.10-11 et G = 7.10-11 uSI ou m3 kg-1
s-2, avec une énorme incertitude relative.
Le bogue logiciel sur le calcul de la date est corrigé. La
constante de temps R7 C3 du filtre passe-bas est ramenée à
5 secondes pour que l’électronique réagisse plus vite. Le
montage est resté en service, du samedi au lundi, sans que l’asservissement
en perde le contrôle. Nous notons de sensibles variations de la période
T0 asservissement du pendule de torsion sous asservissement :
11 s (moyenne sur 3 périodes), puis 10,2 - 11,4 - 10,4 s, puis
12,4 et 12,6 lorsque le pendule est très amorti ; 8,6 s pour le
pendule au début de son amortissement, une minute après la
prise de contrôle par l’asservissement. Cela ne nous facilite pas
la tâche , car T0 asservissement sert au calcul de la constante de
gravitation, mais est aussi la durée pendant laquelle doit se faire
une mesure pour obtenir la valeur moyenne sur une période de la
tension de sortie. C’est peut-être dû au fait que le système
photoélectrique ne travaille pas tout à fait dans sa zone
de linéarité. Cette fois ci, nous approchons deux masses
M extérieures de 20 kg.
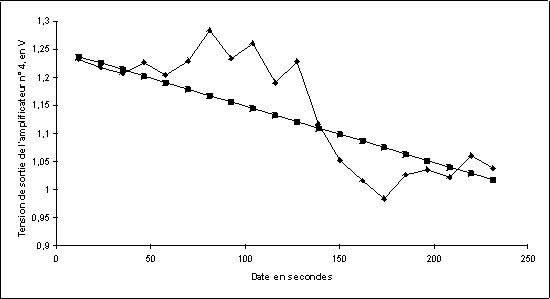
Figure 17. Le montage réagit. Une deuxième série de mesures n’a pas donné de résultats concluants. Serait-ce parce que la récréation venait de sonner, entraînant une cavalcade dans les couloirs ?
C’est notre première mesure en direct, devant un public (nombreux
et discipliné). Les deux masses M de 20 kg sont approchées
au plus près, à environ 13,3 cm des masses m, de centre de
gravité à centre de gravité.
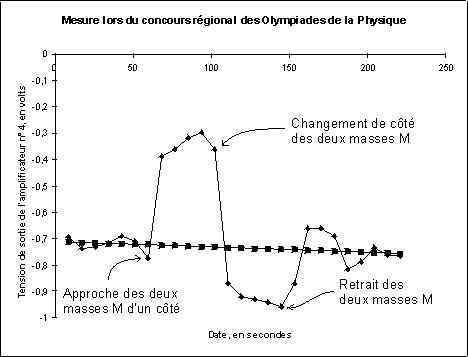
Figure 18. La tension varie de 0,573 V lorsque les masses M passent
d’un côté à l’autre, dérive de la tension déduite.
Notons une dissymétrie dont l’origine est inconnue. Voici les autres
valeurs numériques nécessaires au calcul :
Masse m : 1,05 kg, masse M : 20 kg, diamètre des masses m :
6,2 cm (mais elles présentent des défauts de moulage), distance
axe - centre de gravité des masses m : 8,3 cm, distance axe - milieu
du faisceau lumineux de l’optocoupleur : 11 cm, moment d’inertie calculé
du bras mobile : 0,0153 kg.m2 , efficacité due aux interactions
entre une masse M et les deux masses mobiles m : 75,6 %, période
propre d’oscillation du pendule de torsion, sous l’effet de l’asservissement
: évaluée à 8,3 s, mais le battement observé
lorsque les deux masses M sont très éloignées nous
fait penser que cette période est plus proche de 10 s.
Gain des différents amplificateurs, en valeur absolue, et aux
basses fréquences qui nous intéressent, 1, 5, 1, 10 sans
oublier le gain de 2 fois apporté par le fait que, l’ordinateur
mesurant u4 - (-u4) pour diminuer les bruits, trouve 2.u4. Sensibilité
du phototransistor : 14 410 V.m-1.
Nous calculons, selon la troisième méthode, pour la constante
de gravitation universelle 7,32 . 10-11 uSI, soit une erreur
de 10 %, avec sans doute beaucoup de chance.
Il est difficile de calculer les incertitudes apportées
par notre montage, car beaucoup de facteurs non contrôlables interviennent,
impuretés et irrégularités de forme des masses de
plomb, variation de la sensibilité du phototransistor, et surtout
fluctuation importante de la période propre du pendule de torsion
sous asservissement, de 8 à 12 secondes, cette période intervenant
par son carré, ce qui peut faire varier le résultat dans
un rapport 1 à 2,25, soit de 50 %, autour du résultat moyen.
En cas de doute, il sera prudent de retenir une valeur moyenne de 10 secondes.
Retour en haut de cette page
Remarquons que nous utilisons l’extrémité de la zone
où le comportement du phototransistor est linéaire, puisque
nous comparons cette tension à 0 V. Par la suite, une chute de la
sensibilité du montage, liée aux nombreuses manipulations
des composants photo électriques, nous obligera à modifier
la valeur de la résistance R0 en branchant en parallèle sur
la résistance de 2 200 ohms une résistance de 4 700 ohms,
ce qui changera la sensibilité. Dans ce cas, des tensions de -8,86
à +7,75 V sont obtenues en sortie du phototransistor. La sensibilité,
dont le détail du calcul a déjà été
donné, est, en sortie de l’amplificateur n° 4, de 730 265 Vm-1
(résultat moyen de 20 mesures, avec un écart type de 5 %).
Nos enregistrements sont encore victimes de fluctuations importantes.
Nous cherchons à les diminuer. Les raisons en sont les vibrations
parasites difficiles à éliminer en présentation publique,
les oscillations transversales du pendule, dont la période n’est
pas le quotient exact de la période d’oscillation de torsion par
un entier (et que le calcul de moyenne ne peut donc éliminer) et
les influences extérieures (électrostatiques, électromagnétiques
... ) L’augmentation importante de la masse mobile a réduit leur
importance ; nous avons changé l’écran de notre ordinateur,
un modèle ancien apportant beaucoup de perturbations.
Nous continuons à optimiser le montage. C’est beaucoup plus facile, maintenant qu’il fonctionne.
Lorsque la palette liée à la barre portant les deux masses
m se déplace de x dans l’optocoupleur, le moment de la force magnétique
exercée par la bobine sur l’aimant, par rapport à l’axe de
rotation, varie de M F/delta = s G2 k R x /
R4 , où s est un coefficient d’interaction entre la bobine
et l’aimant, non calculable ou mesurable facilement, proportionnel au nombre
de spires de la bobine (200 ici), G2 le gain de l’amplificateur n°
2 (5 ici, en basse fréquence), k la variation de tension aux bornes
de la résistance R1, en sortie du phototransistor pour un déplacement
d’un mètre de la palette liée au bras mobile (14 410 Vm-1
ici), R4 la valeur de la résistance en série avec la bobine
(1 470 W ici), R la distance entre l’axe de rotation D et le centre de
gravité d’une masse m (0,083 m ici) et x le déplacement de
la palette en mètres. Ce qui peut s’écrire s G2
k
R2 alpha / R4
où a est l’angle de rotation autour de l’axe Delta, ou encore
n alpha , avec n = s G2 k R2 / R4 . Si
on pose le moment d’inertie , J ~ 2 m R2, l’équation
différentielle régissant le mouvement est J @'' + n
@ = 0 qui conduit à une période propre . Nous décidons
de fixer T0 asservi = 10 secondes, pour que la manipulation soit assez
rapide (chaque mesure de valeur moyenne dure T0 asservi et c’est aussi
la durée nécessaire pour que le bras mobile effectue une
oscillation complète autour de sa nouvelle position d’équilibre,
si les deux masses M sont approchées rapidement). Cela conduit à
n = (2 Pi / T0asservi)2 J
ou s R2 (G2 k / R4) =
(2 Pi / T0asservi)2 . 2 m R2. La longueur
du bras mobile, 2R n’intervient donc pas, en fait un peu puisque nous avons
vu que M attire les deux masses m, si R est trop petit.
Si m est multipliée par 10, il faut que G2 soit multiplié
par 10 (mais en ce cas, les non linéarités sont atteintes
plus vite), ou que R4 soit divisée par 10, mais dans le cas de notre
montage, nous ne devons pas descendre au-dessous de 470 W, ou que s soit
multiplié par 10, en augmentant le nombre de spires de la bobine,
ou la taille de l’aimant.
Retenons la première solution : Si on approche M de m, les forces
de gravitation sont multipliées par 10, mais n l’étant aussi,
l’angle de rotation du bras mobile reste le même. La variation de
la tension de sortie de l’amplificateur n° 4 est multipliée
par 10, à cause du gain G2. Ainsi, contrairement au montage classique,
il faut choisir des masses mobiles m importantes.
Il y a des limites à cette augmentation : l’apparition plus
rapide des non linéarités de l’amplificateur n° 2 rend
la manipulation de plus en plus délicate. Nous avons vu que dans
notre montage actuel, avec des masses mobiles de 1,05 kg, l’amplitude des
oscillations, une fois le pendule sous contrôle de l’asservissement,
correspond à un déplacement total, crête à crête
de 8 microns dans l’optocoupleur. Il semble difficile d’espérer
mieux dans une présentation publique, et dans une salle dont nous
ignorons actuellement les caractéristiques.
Calculons le déplacement x d’une masse m et donc de la palette
mobile dans l’optocoupleur, sous l’effet de l’approche d’une masse M :
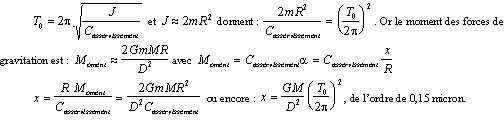
Pour augmenter x, il faut augmenter les masses M extérieures
(c’est fait), les rapprocher (diminuer D) et augmenter T0 (asservi), période
propre de l’oscillateur de torsion sous l’effet de l’asservissement, mais
nous avons choisi sa valeur pour accélérer la manipulation.
x étant imposé, l’augmentation de sensibilité se fera
par augmentation des gains du phototransistor, de l’amplificateur n°
2, de l’amplificateur n° 4 (mais leur régime non linéaire
sera plus vite atteint), tout en gardant la valeur choisie pour T0, ce
qui impose soit d’augmenter la valeur m des masses mobiles, soit de diminuer
l’intensité traversant la bobine, par augmentation de la résistance
R4.
Nous décidons pour la présentation à Paris de
construire un support tournant pour les deux masses M, ce qui en raison
de la symétrie limitera la déformation du sol au cours de
leur rotation.
Nous décidons aussi de réduire la constante de temps
R7 C3 du filtre passe bas, de 5 à 1 seconde, pour accélérer
la réaction de l’électronique, et d’ajouter une fenêtre
transparente permettant d’observer le bras mobile : le jury de Besançon
nous l’a demandé. Nous avions au départ écarté
cette solution, car d’une part la lumière extérieure fausse
les mesures, d’autre part la fenêtre en matière plastique
peut créer des forces électrostatiques importantes. De plus
les oscillations du bras mobile ont une amplitude de quelques microns et
les seules oscillations visibles à l’œil nu sont les oscillations
parasites.
D’autres améliorations sont possibles, mais nous n’aurons pas
le temps en trois semaines de les appliquer :
Le support rotatif pour les deux masses M une fois réalisé,
il devient plus facile de répéter les mesures. Rappelons
que nous mesurons la tension de sortie u4 de l’amplificateur n° 4,
de laquelle est soustraite la tension opposée, soit 2 u4. La mesure
dure une période d’oscillation du pendule de torsion sous l’effet
de l’asservissement, et c’est la valeur moyenne qui est conservée.
La sensibilité du phototransistor est maintenant de 14 605 V.m-1,
à 5 % prés, la constante de temps R7 C3 de 1 seconde.
Nous avons mesuré 7 points, les masses M étant placées
selon une direction perpendiculaire au support des masses mobiles m, ce
qui revient à les éloigner, en raison de la symétrie
des forces exercées. Pendant la mesure du 8° point, nous avons
rapproché les masses M d’un côté (ce point a été
éliminé des calculs). Nous avons alors mesuré 7 points,
puis pendant la mesure du 16° point (éliminé), nous avons
changé les masses M de côté. Lors de la mesure du 24°
point (éliminé), nous avons ramené les masses M à
leur position initiale. La mesure s’est poursuivie jusqu’au 31° point.
Les 7 premiers et les 7 derniers points nous ont donné par régression
linéaire la droite de tendance à la dérive du montage,
droite par rapport à laquelle nous avons calculé le décalage
moyen en tension des autres points, d’un côté et de l’autre.
Nous en avons déduit une valeur de la constante de gravitation universelle.
Voici nos résultats en 10-11 uSI :
7,33 7,41 7,84 7,33 8,38 8,05 6,90 7,59 7,28 6,75 8,06 7,01
Leur moyenne est : 7,49 . 10 -11
uSI, soit 12 % trop grande, avec un écart type de 0,48 . 10
-11 uSI, soit de 6,4 %, pour 7 points retenus.
Pour 2 points, nous avons trouvé 8,30
. 10 -11 uSI avec un écart type de 11,3 % et pour 1 point,
8,76 . 10 -11 uSI avec un écart de 17 %. L’écart
type augmente lorsque le nombre de points de mesure diminue, ce qui est
normal. Par contre, la constante trouvée augmente aussi dans ce
même cas, pour une raison qui nous échappe. Serait-ce parce
que la fréquence de déplacement des deux masses M se rapproche
de la fréquence d’oscillation du pendule de torsion ?
Retour en haut de cette page
Notre souhait initial était de contacter la firme Leybold,
pour lui parler de notre projet, ainsi que des laboratoires de recherche
travaillant actuellement sur la mesure de la constante de gravitation universelle.
Celle-ci a une importance fondamentale dans la constitution de l’univers,
mais nous voulions en savoir plus.
Le catalogue Leybold comporte une description très détaillée
de leur montage de Cavendish, nous n’avons donc pas eu besoin de prendre
contact pour l’instant.
Nous avons commencé la consultation des sites Internet des laboratoires
étudiant ce sujet. Nous y avons trouvé le montage original
de Cavendish, ainsi que deux montages dérivés, améliorés,
actuellement en cours d’expérimentation. Dans l’un, une fibre de
silice est refroidie à 4 K pour éviter les dérives
et les frictions internes (ces dernières augmentent la valeur mesurée
de G), dans l’autre, un asservissement empêche la torsion de la fibre,
montée sur un plateau tournant en même temps que le pendule
de torsion, et c’est l’accélération de la masse mobile qui
est mesurée. Dans les deux, la masse mobile est une plaque
en forme de pavé plat, ce qui permet de rendre la mesure indépendante
de la taille, de la masse et de la distribution de masse du pendule, diminuant
les incertitudes.
Nous avons découvert l’expérience VIRGO qui se propose
de détecter les ondes de gravitation émises par des phénomènes
cosmiques très violents, supernovae, collisions d’étoiles
à neutrons ou de trous noirs et qui constitue un défi scientifique
et technique, puisque la précision des mesures nécessaires
équivaut à détecter une variation de la taille d’un
atome, sur la distance Terre Soleil. D’autres expériences de même
nature sont en cours d’installation dans d’autres pays, ce qui constituera
un réseau mondial ouvrant une nouvelle fenêtre d’observation
en astrophysique.
Nous avons aussi découvert que la constante de gravitation universelle
pose un problème aux physiciens : Non seulement elle n’est pas connue
avec une grande précision, contrairement aux autres constantes physiques,
mais en 1 998, les physiciens ont dû revoir à la hausse les
incertitudes sur sa mesure, qui sont passées de 0,013% (1 987) à
0,15 %.
Retour en haut de cette page
Il nous est parfois arrivé d’être découragés,
mais nous ne regrettons pas d’avoir poursuivi nos efforts, car notre montage
semble enfin fonctionner et donner l’ordre de grandeur de la constante
de gravitation universelle, dans les conditions d’une présentation
publique. La manipulation est rapide, la vitesse de réaction de
notre système de mesure, quelques secondes, nous surprend encore,
mais les incertitudes sont importantes.
Le matériel employé est facile à réaliser
sans outillage particulier, ni matériau difficile à se procurer.
Les grosses masses de plomb sont cependant de transport peu commode.
Nous allons mesurer à nouveau la sensibilité du détecteur
photoélectrique qui a dû changer à la suite des nombreuses
modifications du montage, afin d’améliorer la précision de
nos mesures.
En relation avec notre conseiller scientifique, Daniel Van Labeke,
nous procéderons ultérieurement à un test dans le
laboratoire anti-vibrations de la faculté des sciences de Besançon.
Nous contacterons aussi des chercheurs impliqués dans l’expérience
Virgo.
Tout notre travail est publié sur Internet (ce mémoire,
les détails techniques du montage, le code source du logiciel de
mesure).
Nous remercions le Jury des épreuves de Besançon, nos
conseillers scientifiques Dominique Obert et Daniel Van Labeke, pour leurs
remarques judicieuses et leurs encouragements. Nous remercions aussi tous
les organismes qui par leur concours financier nous ont permis de réaliser
cette expérience, ainsi que l’Administration et l’Intendance du
lycée Xavier Marmier qui nous ont toujours apporté leur soutien.
Retour en haut de cette page
Nous avons modifié les réglages du système
photoélectrique, car la sensibilité de celui-ci avait diminué
suite aux nombreux démontages subis, et le montage ne fonctionnait
plus dans la zone de réaction linéaire du phototransistor.
Pour cela, nous avons diminué la valeur de la résistance
R0 protégeant la diode électroluminescente infra rouge, de
2 200 à 1 500 W. Voici les deux courbes de sensibilité comparées
:
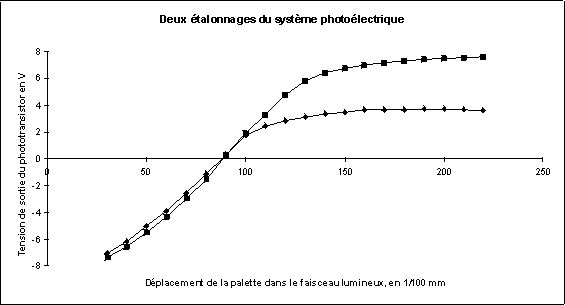
La première courbe, la plus basse, devait être encore plus
basse, sur la fin. Sachant que cette tension est comparée à
0 volt, notre montage devrait être, après modification, plus
sensible et surtout d’un comportement plus linéaire. C’est bien
le cas : L’augmentation de sensibilité (maintenant 14 605 V.m-1,
à 5 % prés en sortie du phototransistor, soit 1 460 000 V.m-1
en sortie de l’amplificateur 4 plus le changeur de signe) a produit une
diminution de la période des oscillations de torsion ; nous avons
donc augmenté la résistance R4 de 1 470 à 5 200 W,
pour tendre vers les 10 secondes souhaitées. Nous observons aussi
que la valeur de cette période fluctue beaucoup moins qu’avant ;
elle mesure maintenant 9 secondes à quelques dixièmes près.
Nous avons ensuite effectué, dans un local très calme,
un enregistrement classique de la tension u4 - ( -u4) durant une manipulation
de mesure de la constante de gravitation, sans calculer directement une
valeur moyenne sur une période de 9 s. La base de temps est moins
précise dans ce cas, car Windows interrompt parfois nos mesures,
mais cela permet de ‘voir’ ce qui se passe à l’approche des deux
masses extérieures M. En ordonnées figurent les tensions
mesurées, en volts, et leur conversion en valeur du déplacement
du centre de gravité des masses mobiles m, en micromètres.
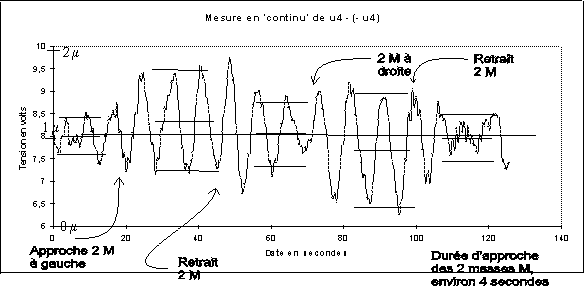
Nous constatons que les masses mobiles m oscillent déjà
au début de l’expérience.
L’approche des deux masses M ‘à gauche’ augmente l’amplitude
des oscillations du pendule de torsion, et décale la position moyenne
de ce pendule, dans le sens attendu (la palette sort un peu du faisceau
lumineux, la tension en sortie du phototransistor, entre l’entrée
non inverseuse du suiveur 1 et le - 9 V augmente, ainsi donc que
u4 - ( -u4) puisqu’il y a ensuite deux changements de signes successifs.
L’éloignement des masses M (en fait nous les plaçons
sur l’axe de symétrie du montage, pour que les couples de forces
s’opposent) diminue l’amplitude des oscillations ainsi que la tension moyenne
de sortie.
L’approche des deux masses M ‘à droite’ augmente l’amplitude
des oscillations du pendule de torsion, et décale la position moyenne
de ce pendule (il tend à entrer dans le faisceau lumineux).
Puis nous éloignons les masses M et la tension moyenne remonte,
l’amplitude des oscillations de torsion diminue.
Nous observons aussi (cela n’est peut-être pas très visible
sur la copie ci-dessus) que les déplacements des masses M provoquent
une augmentation de l’amplitude des oscillations parasites du type pendule
pesant. Cela est dû, entre autres, à la dissymétrie
du montage qui ne comporte qu’une bobine et un aimant. En mettre deux pour
rétablir la symétrie compliquerait considérablement
le montage et nous ferait nous écarter totalement de notre idée
de départ qui était de construire un appareil aisément
reproductible dans tout laboratoire de physique d’un lycée.
Rappelons nos résultats
numériques en 10-11 uSI, obtenus en local calme :
La moyenne de 10 mesures est
: 7,49 . 10 -11 uSI, soit 12 % trop grande, avec un écart
type de 0,48 . 10 -11 uSI, soit de 6,4 %, pour 7 points retenus,
à l’infini, à gauche, à l’infini, à droite,
à l’infini, donc en tout 39 points
Pour 2 points de chaque côté,
nous avons trouvé 8,30 . 10 -11 uSI avec un écart
type de 11,3 % et pour 1 point, 8,76 . 10 -11 uSI avec un écart
de 17 %.
Les incertitudes sont difficiles à calculer, car beaucoup de
paramètres interviennent. Nous les estimons à environ 20
% et nous avons constaté que l’écart type sur une série
de mesures augmente beaucoup en présence de public. Mais ce qui
semble ressortir c’est que les résultats sont systématiquement
trop grands.
Le groupe de professeurs américains a obtenu pour G (7,5 ±
1,5) x 10-11 (mks). Nous ne savons pas comment ils ont estimé,
ou calculé, leur incertitude.
Nous ne connaissons pas la durée exacte de leur mesure, mais
sachant qu’ils ont employé une constante de temps électronique
de 50 secondes, il est raisonnable de penser qu’il leur a fallu au moins
3 x 50 s de chaque côté, soit 5 minutes. Curieusement cette
durée et leur résultat correspondent à notre série
de mesures avec 7 points retenus de chaque côté.
Cela nous a amené à nous demander s’il n’y aurait pas
dans notre montage un phénomène que nous avons négligé
et qui serait responsable de cet écart systématique
vers le haut.
Nous avons tenté une simulation numérique du comportement
du montage ; elle n’est pas au point, mais indique que peut-être
les oscillations parasites du type pendule pesant pourraient augmenter
la valeur de G mesurée, dans certains cas.
Rappelons que ceci revient à mesurer un déplacement moyen
de 0,1 m du centre de gravité des masses mobiles m, et que la fluctuation
de 6,4 % sur cette valeur correspond à 7 nanomètres, ou encore
à une rotation du pendule de torsion de 7.10-9 / 0,083 = 8.10-8
radian ou 0,02 seconde d’arc (2 / 100 ’’).
Notre projet est maintenant d’affiner la simulation numérique
et de modifier encore un peu le montage, pour tenter de vérifier
si la loi de la gravitation universelle est en inverse carré des
distances des masses, ou en inverse, ou encore en inverse du cube. Cela
ne sera pas prêt pour la présentation à Paris - nous
sommes le 15 Novembre - mais pourra peut-être l’être si nous
sommes retenus pour une présentation ultérieure, et pourquoi
pas les olympiades européennes ?
Retour en haut de cette page
· Le remplacement du fil en Nylon par un fil métallique
(argent, bronze... ) devrait limiter sérieusement les dérives
qui nous ont beaucoup gêné.
· Cela permettrait peut-être de se passer de l’asservissement,
dont le principal défaut est d’introduire une dissymétrie
dans le montage, du moins si on emploie une seule bobine et un seul aimant.
Cette dissymétrie provoque des oscillations parasites de pendule
pesant qui sont peut-être la cause de l’erreur systématique
sur le résultat de nos mesures. En ce cas, il faudra choisir un
fil de plus gros diamètre, pour que la période des oscillations
de torsion soit de 10, ou 5 secondes.
· L’emploi d’une carte d’acquisition plus performante permettrait
de supprimer le dernier étage amplificateur, qui est toujours le
premier à saturer. Cela ne devrait pas être difficile car
nous employons une vieille carte de marque Candibus, numérisant
sur 12 bits, entre - 5 V et + 5 V, avec un bruit de fond de 50 mV.
· Ce montage pourrait même n’être employé
que de manière qualitative, pour monter le décalage du pendule
de torsion, lors de l’approche de masses extérieures (voir figure
20). Sa constante de temps électronique n’est plus que de 1 seconde
et sa période de 9 secondes pourrait être abaissée
à 5 secondes, avec de meilleurs composants.