Il s'agit de faire comprendre progressivement comment le physicien
ou la physicienne développe son approche de la réalité
:
// Il s'agit d'une spirale en acier, de section rectangulaire, qui
sert, si je ne m'abuse, à fabriquer les segments de moteurs à
explosion.
Observez des oscillations transversales et longitudinales. Ont-elles les mêmes célérités ? La célérité change-t-elle si on tend le ressort ? Évaluez la pertinence de vos mesures (moyenne, écart-type) et de vos conclusions.
Cette étude sera l'occasion d'utiliser un oscilloscope numérique,
puisque cela figure dans les compétences exigibles du baccalauréat
expérimental.
Nous employons comme capteur, des buzzers piézo-électriques.
Deux buzzers sont plaqués à chaque extrémité
d'une barre longue d'environ 1 mètre. Ils sont serrés à
l'aide d'un simple élastique. Ces buzzers sont raccordés
aux deux entrées d'un oscilloscope numérique. Une extrémité
de la barre est frappée à l'aide d'une règle à
section carrée en aluminium .
La barre peut être constituée de divers matériaux,
bois (chutes de frisette en sapin), panneau aggloméré, acier
(banc d'optique retourné)...
A propos des buzzers : Achetez des buzzers (HPE 127 ou 227) sans
oscillateur intégré (ce sont ces composants qui servent à
faire Bip à tout propos, dans beaucoup d'appareils, ordinateurs,
montres, multimètres, chronomètres...). Ce sont des disques
métalliques sur lesquels est déposé un matériau
piézo-électrique. Ils ont des propriétés bien
curieuses : Ils travaillent par flexion de la lame métallique ;
leur tension de sortie est limitée à - ou + 15 V, ce qui
est sage, en cas de choc involontaire. Un cristal piézo-électrique
d'allume gaz délivre lui des milliers de volts, ce qui ne serait
guère apprécié de l'électronique. Une surcharge
de 400 g donne environ 10 V. Mais cette tension chute rapidement, par décharge
à travers l'appareil de mesure. Ils sont très sensibles à
la température. Vous trouverez d'autres idées de montages,
dans un ancien ouvrage de l'auteur de ce site : "Nouveaux programmes de
Physique, classe de seconde, avec fiches de travaux pratiques" CNDP, CRDP
de Franche-Comté. 1994. Il s'agit en fait des programmes de la précédente
réforme.
Vous pouvez aussi employer les buzzers Electrome qui servaient à
l'étude des sons dans l'ancien programme de seconde.
Les indications suivantes concernent les oscilloscopes de marque
Tektronix, des buzzers Electrome et des barres en bois sec, ou en acier
de plus de 1,2 mètre de long. Les réglages indiqués
en gras sont impératifs, les autres servent à tester que
l'oscilloscope n'a pas été totalement déréglé
précédemment.
1,2 m de bois, vibration transversale, Dt
= 250 ms, v = 4800 m s -1 ;
1,2 m d'acier (ou de fer ? ), vibration transversale, Dt
= 190 ms, v = 6300 m s -1.
Dans le sol de la classe, j'ai personnellement trouvé (avec
de très grandes fluctuations) 3500 m s -1 dans la direction
des poutrelles et 1800 m s -1 dans la direction perpendiculaire
des hourdis.
Lancez le logiciel liravi (Lire Avi, disponible gratuitement sur
ce site) ou tout autre capable de lire un fichier Avi. Ouvrez le fichier
chutePoint.avi. Il représente la chute d'une gomme, filmée
par notre caméra vidéo. Étalonnez le logiciel de mesure.
Relevez les positions successives de la gomme et transférez-les
dans Excel.
Représentez graphiquement :
Pour cela, voici quelques pistes :
Lors de la prochaine interrogation orale, il vous sera demandé
de résumer le contenu de vos travaux.
Pierre jetée dans l'eau, que se passe-t-il ?
Bobine de rail, rappelez vos constatations.
Corde tendue, la célérité dépend-elle de
la tension ? (Expérience qualitative de cours).
Cuve à ondes.
On appelle onde mécanique
le phénomène de propagation d'une perturbation dans un milieu,
sans transport de matière.
Une onde se propage,
à partir d'une source ponctuelle, dans toutes les directions qui
lui sont offertes.
// Note aux professeurs : Je ne suis pas personnellement
d'accord avec l'affirmation du programme officiel qui omet que la source
doit être ponctuelle : Si on jette une pierre dans l'eau,
c'est effectivement vrai, mais la source est quasi ponctuelle. Si la source
est large (par rapport à la longueur d'onde qui sera abordée
à la leçon suivante), elle peut émettre une onde directive.
C'est le vieux débat de l'ancien programme de seconde qui resurgit,
à l'envers. L'ancien programme décrétait les ultrasons
directifs, contrairement aux sons audibles, alors que la seule différence
réside dans la taille relative de la surface émettrice, par
rapport à la longueur d'onde. Pour rendre un son audible directif,
il faut augmenter la taille du haut parleur, ou combiner convenablement
plusieurs haut parleurs ; c'est ce qui se fait dans les concerts de plein
air, avec les châteaux d'enceintes acoustiques.
Mais le contraire d'une déclaration fausse n'est
pas forcément juste ; on sait réaliser des sources
d'ondes directives (échographie, lithotriteur ou lithotripteur,
laser), et en tout cas qui n'émettent pas vers l'arrière,
même si on peut chipoter sur le phénomène de diffraction.
La perturbation se transmet de proche en proche ; il y a transfert d'énergie, sans transport de matière.
La célérité d'une onde (vitesse de propagation de la perturbation) est une propriété du milieu dans lequel elle se propage.
Deux ondes peuvent se croiser sans se perturber.
Cette dernière propriété peut être observée à la surface de l'eau, en y jetant 2 pierres, ou sur la cuve à ondes, en faisant réfléchir une onde "plane" sur un "miroir" incliné par rapport à la direction de propagation et en s'arrangeant pour que l'onde réfléchie se sépare bien de l'onde incidente.
// Note : Cette propriété suppose la linéarité du milieu de propagation.
// Note : Nous supposons le milieu non dispersif, ce qui
permet à l'onde de se propager sans changer de forme ; nous supposons
de plus qu'il n'y a pas d'atténuation.
Étudions une perturbation qui se propage le long d'une corde. Nous dirons qu'il s'agit d'une onde progressive (elle avance le long de la corde), à une dimension.
Soit un point M de la corde. Nous savons de quel point de la corde il
s'agit, dès que son abscisse x est connue. La perturbation p en
ce point M dépend de la date t. Cette perturbation p, à la
même date, n'est pas la même en un point M' situé plus
loin sur la corde, dans le sens de propagation.
à t égale, p(M) est différent de p(M').
La valeur de la perturbation dépend donc à la fois de la date t et de la position x.
Si le signal ne se déforme pas, la perturbation en M' est en
retard par rapport à la perturbation en M.
P(M') à t' égale p(M) à t, avec t' > t.
Nous pouvons écrire t' = t + t,
où t est le retard, avec
t = MM' / v
v étant la célérité de l'onde.
Une onde est longitudinale
si la perturbation et la propagation ont même direction ;
une onde est transversale
si la perturbation a une direction perpendiculaire à celle de la
propagation.
Sur le Bordas.
Page 33 et suivantes, exercices 17, 19, 20, 22, 23, 28, 30 (niveau
Bac).
// Note : Cette séquence pose un petit problème
: Normalement, avec la précédente et la suivante, les élèves
ne doivent avoir que deux séances de travaux pratiques. Nous avons
donc essayé d'alléger le contenu. Ceci étant, beaucoup
de notions fondamentales de physique sont abordées ici, et il faut
y consacrer le temps qu'elles méritent.
La cuve à ondes permet des expériences très
convaincantes
Une onde progressive sinusoïdale présente
Montrez sur la cuve à ondes, la diffraction d'ondes linéaire
et circulaire par un trou ;
montrez l'influence de la largeur du trou,
à largeur du trou égale, montrez que plus la longueur
d'onde est grande, plus l'angle de diffraction est grand, et que la grandeur
caractéristique est la longueur d'onde.
faites remarquer que l'onde diffractée a même longueur
d'onde que l'onde incidente, et donc même fréquence ;
montrez la diffraction par un bord d'écran et par un obstacle.
Demandez aux élèves de se remémorer une expérience
de seconde, utilisant la diffraction.
La diffraction est
un écart à la loi de propagation rectiligne d'une onde ;
elle se manifeste si
les dimensions d'une ouverture, ou d'un obstacle sont du même ordre
de grandeur que la longueur d'onde.
La diffraction est un
phénomène caractéristique des ondes.
// Veuillez noter que le programme officiel n'évoque pas la propagation
rectiligne.
// La phrase : "elle se
manifeste si les dimensions d'une ouverture, ou d'un obstacle sont du même
ordre de grandeur que la longueur d'onde" est conforme au
programme officiel. Elle est fortement contestable. La diffraction
se manifeste toujours. Sur la cuve à ondes, de faibles dimensions,
elle n'est notable que dans le cas évoqué. Lorsque l'ouverture
a une taille de l'ordre de l, le faisceau diffracte
selon un angle important. En optique, où les distances d'observation
sont souvent considérables par rapport à l,
elle se manifeste même pour des ouvertures plusieurs milliers de
fois plus grandes que l. Consultez à
ce sujet notre sujet d'Olympiades
de la Physique : "Correction de l'aberration chromatique d'une lentille
réfractive par une lentille diffractive".
Sur la cuve à ondes, avec une faible hauteur d'eau, faites
observer que la célérité de l'onde dépend de
sa fréquence (Cela sera l'objet de la deuxième partie du
travail pratique). Essayez de mettre en évidence l'effet d'un dioptre,
déviant différemment les ondes rectilignes selon leur fréquence.
Demandez aux élèves d'imaginer ce qu'il advient d'un signal qui se propage dans un milieu dispersif. Comment corriger cette dispersion si un signal se propage le long d'une très longue fibre optique ?
Si la vitesse de propagation
d'une onde dépend de sa fréquence, on parle de dispersion.
Le milieu est alors dispersif.
Pour chaque groupe de deux élèves :
Ce travail pratique n'est pas aussi simple à interpréter
que ce que pourrait faire croire une analyse superficielle. Si vous n'êtes
pas convaincu de cela, modifiez le montage en plaçant l'émetteur
raccordé à la voie 1, à droite ; ou bien laissez-le
à gauche, et synchronisez sur la voie 2. En fait, la courbe 2 ne
se déplace dans le même sens que le récepteur, que
si les bonnes conventions, liées à notre manière d'écrire,
de gauche à droite, sont respectées.
De plus, le déplacement sur l'écran n'a pas la valeur du déplacement du capteur. Enfin, tout ce qu'on observe est lié à la synchronisation de l'oscilloscope. L'intérêt de cette expérience est de faire à nouveau manipuler l'oscilloscope.
Essayez de refaire la manipulation avec un oscilloscope numérique, en mode monocoup ; l'interprétation sera moins simple, mais sans doute plus proche de la réalité physique.
Alimentez l'émetteur ultrasonore, mesurez sur l'entrée
1 de l'oscilloscope, la tension appliquée à l'émetteur
; réglez la synchronisation de l'oscilloscope sur la voie 1.
Raccordez le récepteur sur la voie 2.
Respectez impérativement l'ordre logique de branchement : émetteur
à gauche, récepteur à droite.
Mesurez la période des ultrasons, calculez leur fréquence,
mesurez leur longueur d'onde. Sachant que leur célérité
est de 340 m.s-1, la relation
donnant l est-elle vérifiée ?
Comparez la taille de l'émetteur d'ultrasons et la longueur
d'onde ; Le phénomène de diffraction doit-il apparaître
? Si oui, montrez-le. Proposez une méthode permettant avec des émetteurs
identiques à celui dont vous disposez de réaliser une onde
plane, une onde sphérique convergente.
Vous trouverez dans le chapitre logiciel, tout ce qu'il faut pour
cela : Chargez le logiciel LireAvi
(lireavi_z_.exe) qui lit aussi les images fixes au format Bitmap, ou Jpeg.
Chargez les photographies de la cuve à ondes et le texte du travail
pratique (dispers.exe). Dans le logiciel LireAvi, ouvrez le texte du travail
pratique dans le dossier Dispersion ; faites ce qui est demandé.
A titre d'information, voici une version de ce texte (peut-être
pas la plus récente) :
Travail pratique Étude de la dispersion des ondes.
Nous nous proposons d'étudier la propagation d'ondes linéaires, à la surface d'une cuve à ondes. Pour cela, nous disposons de 6 images fixes, nommées ondeP1, à ondeP6, rangées dans le sous dossier ...\Physique\LireAvi\Images.
Ces enregistrements au format compressé Jpeg, peuvent être lus par de nombreux logiciels de dessin, ainsi que par le logiciel Lire Avi, capable d'afficher les images de fichiers aux formats AVI, Bitmap et Jpeg, et de mesurer la position des points indiqués par un clic souris.
Les 6 enregistrements, ondeP1, à ondeP6 ont été réalisés de la manière suivante
Un petit moteur actionnant une pompe, crée une perturbation linéaire, périodique, à la surface d'une cuve à onde. Cette perturbation se propage d'abord dans une "grande" profondeur d'eau (environ 6 mm), puis arrive en biais sur une plaque transparente, qui réduit la hauteur d'eau à moins de 2 mm.
La fréquence de l'onde, est mesurée à l'aide d'une photodiode, reliée à un oscilloscope numérique, et qui détecte les variations de luminosité dues au passage des crêtes brillantes et des creux sombres. Lorsque la fréquence devient relativement élevée (ondeP6), c'est à dire lorsque les crêtes des ondes se rapprochent tellement que la photodiode ne peut plus distinguer des maxima et des minima de luminosité, le stroboscope est mis en service, réglé exactement à la fréquence du générateur, et la photodiode détecte les éclairs du stroboscope. La fréquence correcte F du stroboscope est la fréquence maximale donnant une fixité apparente des ondes, avec une longueur d'onde correcte. A la fréquence 2 F, les ondes semblent fixes, mais leur longueur d'onde semble divisée par deux.
Les fréquences
correspondant aux enregistrements ondeP1, à ondeP6 sont respectivement
6,99 Hz ; 8,62 Hz ; 11,
43 Hz ; 16, 4 Hz ; 21,1 Hz ; 34, 2 Hz.
Une règle en aluminium, à section carrée, longue de 17 cm, est posée dans la cuve, à droite du générateur d'ondes, pour permettre l'étalonnage.
Les images ont été traitées dans un logiciel de dessin, de manière à augmenter leur contraste, en ajoutant de la couleur.
Vous devrez répondre aux questions suivantes
Mesurez la longueur d'onde, et calculez la célérité, pour les 6 fréquences proposées, dans l'eau de "grande" profondeur et dans l'eau de faible profondeur.
La célérité
dépend-elle de la fréquence ? Comment s'appelle ce phénomène
?
Discutez vos résultats,
en tenant compte notamment de la plus ou moins grande facilité de
mesure de la fréquence du générateur d'ondes.
Lorsque l'onde change de milieu (passage de la "grande" à la faible profondeur), elle change de direction. Comment s'appelle ce phénomène ?
Mesurez ce changement
de direction, pour les 6 fréquences proposées. Est-il constant
?
Trouvez un phénomène
équivalent, dans un autre domaine de la physique. Quel nom porte-t-il
?
Si ce changement de direction
n'est pas constant, à quoi l'attribuez-vous ?
Mes résultats personnels :
| f en Hz | 6,99 | 8,62 | 11,43 | 16,4 | 21,1 | 34,2 |
| l1 en m | 0,0288 | 0,0226 | 0,0147 | 0,0101 | 0,00774 | 0,00527 |
| l2 en m | 0,0133 | 0,0123 | 0,00938 | 0,0078 | 0,0063 | 0,00486 |
| déviation en ° | 19,9 | 19,3 | 15,7 | 11,3 | 10,4 | 5,7 |
| v1 en m s-1 | 0,201 | 0,195 | 0,168 | 0,165 | 0,163 | 0,180 |
| v2 en m s-1 | 0,093 | 0,106 | 0,107 | 0,128 | 0,133 | 0,166 |
Conclusion : Dans la partie "profonde" de la cuve,
où la hauteur d'eau est d'environ 5 mm, la célérité
est fonction décroissante de la fréquence, sauf pour le dernier
point de mesure. Dans l'autre partie de hauteur d'eau environ 1 mm, la
célérité est fonction croissante de la fréquence.
Vous trouverez une étude théorique complète
dans les fiches de travaux pratiques Leybold ; vous pouvez aussi consulter
l'article : LAGOUTE C. A propos des ondes de la cuve à ondes. BUP
mars 2003, volume 852, p. 441-852.
La représentation habituellement employée
est v = f (l), célérité
en fonction de la longueur d'onde. Avec notre cuve à ondes, nous
travaillons essentiellement dans les conditions qui donnent des rides capillaires.
lC
= 1,7 cm est appelée longueur d'onde capillaire. Pour
l < lC nous obtenons des
rides capillaires, pour lesquelles la célérité est
fonction décroissante de la longueur d'onde. Pour
l > lC nous obtenons des ondes
de gravité, pour lesquelles la célérité est
fonction croissante de la longueur d'onde. Nos résultats expérimentaux
correspondent assez bien aux calculs théoriques. Seule la valeur
de la longueur d'onde capillaire est trouvée un peu différente
(plus petite, aux alentours de 8 à 15 mm).
Page 50 et suivantes, exercices : 13, 18, 23, 12 (à titre
culturel), 15 (difficile).
Matériel nécessaire :
Pour la diffraction : Laser et support, fente réglable et support,
fentes de largeur connue et support, lampe de bureau basse tension.
Pour la dispersion : Projecteur de diapositives et support télescopique,
pince 3 doigts et support de physique, pour tenir l'objectif du projecteur,
condenseur à 2 lentilles (classique au laboratoire d'optique) et
son support, fente réglable métallique et support, prisme
classique et prisme à vision directe et leurs supports, grande plaque
de bois sur laquelle sera fait le montage.
Expérience de cours avec un laser, des fentes réglables,
fixes de largeur connue, des trous.
Observez la symétrie de la figure obtenue. Pour une fente de
largeur connue, notez la largeur de la fente, mesurez la distance fente
écran et la taille de la figure de diffraction.
Expérience à faire par les élèves en classe
entière ou chez eux : Placez l'un contre l'autre, à la verticale,
deux crayons de papier ; regardez à travers la fente restant entre
les deux crayons (vous profiterez du défaut des crayons en bois
qui ne sont pas tout à fait droits, pour réaliser une fente
de largeur variable selon la force de serrage). Observez par exemple les
montants d'une fenêtre. Que se passe-t-il si vous écartez
ou resserrez les crayons ?
Observez maintenant à travers la fente mise à l'horizontale.
Observez à travers une fente très étroite, une
lampe de bureau à basse tension. Attention à ne pas vous
brûler les yeux. Apercevez-vous des colorations ?
Observez des lampes de rue, la nuit, à travers un voilage.
La lumière subit une diffraction, lorsqu'elle rencontre une
ouverture de très petites dimensions.
La lumière peut donc être décrite comme une onde. On parle du modèle ondulatoire de la lumière.
Notez bien que nous n'avons pas dit que ce modèle rend compte de toutes les propriétés de la lumière !
La lumière se propage dans le vide, à la célérité
c.
La valeur exacte de c est 299 792 458 m. s-1.
Se comportant comme une onde, elle a une longueur d'onde dans le vide,
l
=
c / n, où n
est
la fréquence de l'onde.
l se mesure en mètre, c en mètre
par seconde, et n en hertz. Les longueurs d'ondes
de la lumière dans les autres milieux ne sont pas d'usage courant.
A chaque longueur d'onde de la lumière visible dans le vide
correspond une couleur.
Vérifiez l'homogénéité de la relation précédente.
Vérifiez expérimentalement que dans le cas de la diffraction,
la relation suivante est vérifiée :
|
|
où l est la longueur d'onde de la
lumière dans le vide (très proche de la longueur d'onde dans
l'air), a la largeur de la fente, ou l'épaisseur du fil, et q
l'écart
angulaire entre le milieu de la frange centrale et la première extinction.
Vérifiez l'homogénéité de la relation précédente.
Le vide est-il dispersif ?
// Note au professeur : Il existe de nombreux
montages de spectroscopie. En voici un qui donne de beaux spectres, lumineux
et purs. Il vous demandera un peu d'entraînement, mais vous aurez
peut-être le plaisir d'entendre dans votre dos un élève
dire à voix basse à son voisin : "Il est plus grand que l'année
dernière.". Comme dit une publicité, à tout âge,
les hommes ont éprouvé le besoin de mesurer leurs armes.
Faites le montage suivant sur une plaque de bois ; ainsi, vous pourrez le tourner en bloc, pour envoyer le spectre au bon endroit.
Voici un spectre donné par un prisme, approximativement représenté. Notez que visuellement, les trois bandes rouge, verte et bleue, ne sont pas de la même largeur (un réseau donne 3 bandes de même largeur) et que, si le montage est bien réglé, la bande jaune orange apparaît très étroite.
| 10
400
|
480
|
550
|
600 |
100 m
800 nm |
|
|
U V |
I R | ||||
|
7,5
3 . 1016 Hz |
5 | 3,8
3 . 1012
Hz
|
Par analogie avec l'expérience sur la cuve à ondes
(si elle a donné des résultats convaincants), on peut tirer
l'interprétation suivante :
Les milieux matériels sont (plus ou moins) dispersifs pour la
lumière.
Par définition, l'indice n de réfraction d'un milieu
transparent est le rapport de la célérité c de la
lumière dans le vide, et de la célérité V de
la lumière dans le milieu considéré.
n = c / V
n est une grandeur sans dimensions.
Remarque : n est supérieur ou égal à 1, V est inférieure ou égale à c. La relation est donc facile à retrouver sans erreur.
Si un milieu est dispersif, cela signifie que V dépend de la fréquence de l'onde lumineuse, donc que n dépend de la longueur d'onde de la lumière dans le vide.
Exercice : Trouvez l'indice du vide.
| Milieu matériel | Indice de réfraction | Célérité de la lumière, en m . s-1 |
| air | 1,0003 | 3 . 108 |
| eau | 1,33 | |
| verre | 1,5 à 1,8 | |
| plexiglas â | 1,5 | 2 . 108 |
| diamant | 2,4 |
Exercices : Recherchez des noms de matériaux transparents très dispersifs ou peu dispersifs.
Pages 70 et suivantes : Exercices 11, 13, 19, 24 (Ajoutez : "Dans quel
milieu sont mesurées les longueurs d'onde indiquées, pourquoi
?"), 26 (Type Bac ; ajoutez : "Critiquez l'énoncé").
Vous pourrez consulter votre livre de cours, ainsi
qu'une base de données disponible sur Internet. Recherchez dans
Google le mot clé nubase. Voici une réponse utile : http://www-csnsm.in2p3.fr/AMDC/web/nubase_fr.html
Vous y trouverez un fichier au format ASCII, des exécutables
que vous pourrez installer sur votre PC et même des animations Java.
Voici, à titre indicatif, la fenêtre d'accueil interactive, du logiciel exécutable nucleus.exe, fourni dans nucleus.zip :
Ce logiciel peut être complété par nucwav.exe, fourni dans nucwav.zip, qui ajoute des commentaires sonores sur les familles radioactives. Il suffit que les 2 exécutables soient décompressés dans le même dossier.
Vous pouvez l'installer
en copiant dans un dossier à votre convenance, les fichiers nucleus.zip
et nucwav.zip, et en les décompressant sur place à l'aide
de WinZip, ou d'un décompresseur téléchargeable en
même temps, nommé unzip.exe et qui vous rappellera le bon
vieux temps du DOS et de ses lignes de commande.
Par exemple, si tout est rangé dans C:\Programmes\Nucleaire,
faites Démarrer | Exécuter | Parcourir, trouvez unzip.exe,
puis faites Ouvrir, puis modifiez la ligne de commande en
C:\Programmes\Nucleaire\unzip -d nucleus (et à
la fois suivante : C:\Programmes\Nucleaire\unzip -d nucwav)
et enfin, Validez.
Si rien ne marche, vérifiez qu'il n'y a pas de
faute de frappe et enfin, vérifiez les noms de dossiers. L'espace
de Program Files n'est pas accepté !!!
Les 2 méthodes donnent le même résultat.
L'ensemble du dossier peut être déplacé ou renommé.
Créez une icône de raccourci sur le bureau, pour l'exécutable
nucleus, uniquement.
Mode d'emploi simplifié ![]() .
.
Vous savez qu'un atome comporte :
|
|
|
|
|
|
|
|
L'atome étant neutre comporte aussi Z électrons. Ce numéro atomique Z caractérise l'élément chimique. Tous les atomes et tous les ions d'un même élément ont le même numéro atomique, donc le même nombre de protons.
La masse d'un atome, d'un noyau, d'un nucléon s'exprime en kilogramme
; elle peut aussi s'exprimer en unité de masse atomique.
Par définition, l'unité de masse atomique (symbole
u) est le douzième de la masse d'un atome de carbone 12.
1 u = 1,660 540 2 . 10-27 kg.
Quelques valeurs numériques :
| masse en u | masse approchée en kg | charge approchée en C | |
| proton | 1,007 270 023 | 1,67 . 10-27 | + 1,6 . 10-19 |
| neutron | 1,008 665 842 | 1,67 . 10-27 | 0 |
| électron | 0,000 548 576 | 0,9 . 10-30 | - 1,6 . 10-19 |
Définition
: On appelle noyaux isotopes des noyaux qui possèdent le même
nombre de protons, mais diffèrent par leur nombre de neutrons.
Des atomes isotopes possédant le même nombre de protons, possèdent donc le même cortège électronique ; ils ont les mêmes propriétés chimiques. Un élément chimique est donc constitué d'un mélange d'isotopes (mélange de nucléides).
Elle a été découverte par hasard, en 1896,
par le Français, Henri Becquerel.
Un noyau radioactif est un noyau instable, qui se désintègre spontanément
|
|
2 + | |
|
|
||
|
|
Les particules b-sont
des électrons.
Ils sont émis à une vitesse proche de c, possèdent
une très grande énergie et sont arrêtés par
une plaque d'aluminium. Il ne s'agit pas des électrons du cortège
électronique.
Les particules b+sont
des positons, antiparticule de l'électron.
Ils ont même masse que l'électron et une charge opposée.
Un positon et un électron qui se rencontrent s'annihilent en produisant
un rayonnement g. On peut dire positon ou
positron.
Le rayonnement gest un rayonnement électromagnétique, de très haute fréquence, très courte longueur d'onde (10-4 nm) et très grande énergie. Il est absorbé par une forte épaisseur de béton ou de plomb.
Sur les 350 noyaux naturels, 290 sont stables et gardent indéfiniment
la même structure, 60 sont instables donc radioactifs ; les noyaux
artificiels sont presque tous radioactifs.
Sur la figure en tête de cette leçon, les noyaux connus
sont représentés dans un graphique Z = f (N), où le
nombre de protons Z est selon l'axe des ordonnées, et le nombre
de neutrons N = A - Z, selon l'axe des abscisses.
En noir sont représentés les noyaux stables ; ils forment
une "vallée de stabilité" qui suit la droite Z = N, jusqu'à
Z = 20, puis passe au-dessous, pour Z > 20.
Attention, la représentation inverse N = f (Z) est aussi
employée ; la "vallée de stabilité" passe donc alors
au-dessus de N = Z.
Appliquons ces lois dans les trois cas :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voici trois exemples conduisant tous au plomb 207 :

Exercice 1 : Faites correspondre les 3 flèches aux différents
types de radioactivité.
Exercice 2 : Recherchez dans le logiciel Nucleus.exe, Nubase,
le noyau fils du carbone 14 et la famille radioactive de l'uranium 235.
Nous allons adopter la démarche suivante : premièrement,
nous allons admettre une hypothèse sur la désintégration.
Sans en faire la démonstration mathématique, nous admettrons
une conséquence de cette hypothèse, conséquence que
nous vérifierons expérimentalement, de manière approchée
bien sur. A partir de tout cela, nous démontrerons la loi
de décroissance.
Veuillez noter que tous les raisonnements qui suivent supposent que nous employons une seule espèce de substance radioactive.
Il est impossible de prédire l'instant précis de la
désintégration d'un noyau. Un noyau atomique n'a pas "d'âge".
Il est impossible de discerner des atomes identiques. La désintégration
d'un noyau est un phénomène individuel, sans effet sur les
autres noyaux.
Imaginez que vous placiez dans une boîte des atomes radioactifs non désintégrés, de fabrication ancienne, et dans une autre boîte la même quantité de matière d'atomes radioactifs du même isotope, de fabrication récente. Les 2 boîtes se comporteront identiquement. Si vous placez tous les atomes dans une seule boîte, vous n'aurez fait que doubler la quantité de matière.
A l'échelle de quelques atomes, il est donc impossible de
prédire combien d'atomes se désintégreront pendant
une seconde.
Par contre, si nous considérons un très grand nombre d'atomes, il devient possible d'estimer avec une précision raisonnable combien d'atomes se désintégreront pendant une seconde.
Si la désintégration radioactive a un caractère
aléatoire, et si pendant toute la durée de l'expérience,
le nombre total d'atomes non désintégrés N reste constant
(ce qui veut dire qu'une très faible proportion d'atomes se désintègrent
pendant la durée des mesures), une autre propriété,
liée au caractère aléatoire de la désintégration,
et que nous ne démontrerons pas apparaît :
Supposons que nous mesurions 100 fois de suite, le nombre d'atomes
désintégrés en une seconde (ou en une autre durée
quelconque). Nous ne trouverons pas toujours la même valeur, à
cause du caractère aléatoire. Sur cette série de 100
mesures, nous pourrons calculer la valeur moyenne et l'écart-type.
Si la désintégration a vraiment un caractère aléatoire,
l'écart-type sera (quasiment) égal à la racine carrée
de la valeur moyenne. Nous vérifierons cela en travaux pratiques.
// Attention : Ne confondez-pas cette valeur de N, avec un nombre
de neutrons.
Nous allons maintenant démontrer la loi de décroissance.
Par définition,
l'activité A d'un échantillon radioactif est numériquement égale au nombre moyen de désintégrations |DN| par unité de temps Dt.
A = |DN| / Dt
A se mesure en becquerel (symbole Bq), DN variation du nombre d'atomes pères est négative, d'où la valeur absolue, Dt se mesure en seconde.
Vous comprenez qu'il faut prendre la moyenne de |DN| puisque les valeurs successivement mesurées expérimentalement fluctuent. L'activité de l'échantillon diminuera progressivement, au fur et à mesure de la diminution du nombre d'atomes pères.
Quelques valeurs numériques :
| eau de mer | 10 Bq par litre |
| granit | 1000 Bq par kilogramme |
| corps humain | 8000 Bq |
Compte tenu des propriétés énoncées
au paragraphe précédent, il apparaît que l'activité
A d'un échantillon est proportionnelle au nombre de noyaux de l'échantillon
:
A = l . N
//Notez qu'en posant ceci, nous faisons disparaître l'aspect aléatoire de la radioactivité.
Jusqu'ici, nous avions raisonné sur des expériences réalisées très rapidement, avec donc un nombre N n'évoluant pas ou très peu. En fait, N est fonction de la date t, de même donc que l'activité A. Par contre, l est une constante caractéristique de l'isotope. On l'appelle constante de radioactivité.
De tout cela, en imaginant que les durées de mesure tendent vers la valeur 0, nous déduisons l'expression :
- dN / dt = l . N, ou dN / dt = - l . N, ou encore dN(t) / dt = - l . N(t).
La dérivée de la fonction N(t) par rapport au temps est proportionnelle à cette même fonction N(t). Ceci est caractéristique de la fonction exponentielle.
Posons N(t) = N0 . e k.t ; il vient dN / dt = k . N0 . e k.t ; soit dN / dt = k . N.
Par identification, nous trouvons k = -l.
| Donc le nombre N(t) de noyaux radioactifs, présents à
la date t est donné par : N(t) = N0 . e - l
.
t ;
il est facile de vérifier que N0 est le nombre de noyaux présents à la date 0. |
Le signe moins est caractéristique d'une décroissance du nombre de noyaux au cours du temps.
De ces diverses relations, il ressort que l se mesure en s-1 . Vous pouvez aussi remarquer que l'argument de la fonction exponentielle est obligatoirement sans dimensions.
Par définition, la constante de temps t
=l-1.
N(t) = N0 . e - l
/l = N . e -1 = N / e.
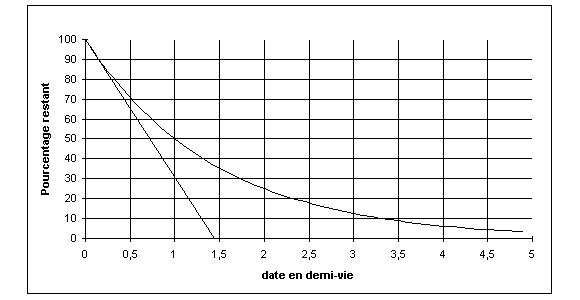
Le temps de demi-vie, t 1/2, est la durée au bout
de laquelle il ne reste que la moitié du nombre de noyaux initial
N0.
t 1/2 = ln (2) . t, ou encore
t
1/2
= 0,69 . t.
Voici représenté en pourcentage de N0, le nombre de noyaux restant, en fonction de la date exprimée en demi-vie. Notez que t vaut un peu moins de 1,5 . t 1/2 (1,44 . t 1/2. en fait).
L'iode 131 utilisé en scintigraphie a une demi-vie de 8,1
jour. On considère un échantillon de 10-12 mol.
Calculons sa masse, son activité et le nombre d'atomes restant après
16,2 jours, puis 1 an. Un détecteur enregistrera-t-il toutes les
réactions nucléaires, pourquoi ?
// Réponses : Le nombre N d'atomes contenus
dans l'échantillon est N ou N0 = 6,02 . 1023
x 10-12 = 6,02 . 1011.
La masse de l'échantillon est de 0,131 x 10 .
10-12 = 1,31 . 10-10 kg. La demi-vie de 8,1 jour
permet de calculer la constante de temps ; de t 1/2 = 0,69 .
t,
nous tirons t = 8,1 x 24 x 3600 / 0,69 = 1,01
. 106 s.
Nous en déduisons l
= t-1 = 9,86 . 10-7 s-1.
C'est la probabilité pour qu'un atome se désintègre
en une seconde.
L'activité donnée par la relation , vaut A = 9,86 . 10-7. 6,02 . 1011 = 5,91. 105 s-1. Remarquez que cela signifie qu'il se produit en moyenne 600 000 désintégrations par seconde, avec un écart-type de (5,91. 105)1/2 ou 769 désintégrations, soit que le nombre de désintégrations mesuré chaque seconde ne s'écarte de la valeur théorique que d'environ 0,1 %. Notez aussi que, par définition, l'écart-type est la racine carrée de la variance.
Après 16,2 jours, il restera 1/4 des atomes, soit
1,5 . 1011.
Après 1 an, soit 365 x 24 x 3600 secondes = 3,15
. 107 s, il en restera : N(t) = N0 . e - l
.
t, avec t = 3,15 . 107 s, soit
6,02 . 1011. x e-31,1 = 0,018 atome.
Ce dernier résultat signifie simplement que nous
sommes sortis du cadre macroscopique, c'est à dire qu'il ne reste
plus de matière radioactive.
Le détecteur n'enregistre pas toutes les désintégrations, car il a une fenêtre d'entrée limitée, et une efficacité inférieure à 100 %.
Applications : Datation, radiothérapie, imagerie médicale,
marquage de molécules pour la recherche en chimie, stérilisation.
Dangers : On parle d'irradiation si un organisme reçoit
le rayonnement émis par une source ; Si l'énergie reçue
dépasse 5 J / kg, la mort survient rapidement.
on parle de contamination si des produits radioactifs sont absorbés
par les voies digestives ou respiratoire. Nous avons vu, que dans ce cas,
les émetteurs a sont très dangereux.
Datation au carbone 14 : Le 614C, radioactif b, est créé dans la haute atmosphère, à partir de l'azote 714N. Il est rapidement oxydé en CO2 qui se mélange à celui de l'air, avant d'être absorbé par les plantes. La proportion 614C, 612C est d'environ 10-12, chez les êtres vivants ; elle diminue après leur mort. 1 g d'échantillon de carbone est nécessaire pour une datation à l'aide d'un compteur Geiger-Müller. Un accélérateur de particules suivi d'un spectromètre de masse permet d'effectuer une datation à partir d'un échantillon de seulement 1 milligramme.
Nous allons utiliser, en groupe, un détecteur de Geiger-Müller
(banc appelé CRAB, de la firme Jeulin), sensible aux rayonnements
a,
b, et g. La source radioactive est un
fragment de césium 137, de demi-vie (appelée aussi période,
bien que le phénomène n'ait rien de périodique) 30
ans. Elle émet les 2 types de particules,
a,
et b, mais une lame d'aluminium permet d'arrêter
les rayons a. Nous ne connaissons pas les caractéristiques
techniques du détecteur Geiger-Müller du banc CRAB, mais vous
trouverez, à la fin du deuxième travail pratique des indications
concernant un détecteur Geiger-Müller
proposé par la firme Leybold.
Il était prévu d'améliorer
ce travail pratique, lorsque nous disposerions du détecteur sensible
proposé par la firme Leybold. Mais ce détecteur n'est plus
disponible, remplacé par un détecteur de marque Gamma-Scout,
fourni avec un logiciel d'acquisition et le cable de liaison à un
ordinateur, matériel disponible aussi chez Conrad électronique.
Notez que des données importantes
sont regroupées à la fin de cet énoncé.
A la question : "Savez-vous à quel rayonnement radioactif, vous
êtes personnellement exposés ?", des élèves
de seconde ont répondu :
Etes-vous d'accord avec ces réponses ?
Nous allons essayer, à l'aide du détecteur de Geiger-Müller,
de mesurer la radioactivité d'un bloc de granit.
Quelle précautions expérimentales faut-il prendre
?
// Réponse : Il ne s'agit pas de mettre des bottes, des masques et des lunettes, voire un casque pour impressionner les naïfs, mais d'isoler autant que possible le compteur des autres sources de rayonnement, puis de soustraire de nos mesures le rayonnement ambiant, ayant, malgré nos précautions, atteint le détecteur.
Expérience en classe : Mesurons pendant 5 secondes, plusieurs
fois de suite, le nombre d'évènements détectés
par le compteur de Geiger-Müller, en l'absence et en la présence
de granit.
Le résultat n'est pas probant. Question : "Comment améliorer
la précision des mesures ?".
// Réponse : Il faut augmenter le nombre
d'évènements détectés, donc la durée
des mesures.
Expérience :
Le banc CRAB de Jeulin est disposé horizontalement. Les plaques
de plomb livrées avec sont posées au-dessus du détecteur,
pour limiter l'influence des rayons cosmiques. Des comptages sont effectués,
sans granit, puis en plaçant au bout du banc CRAB un bloc de granit
d'environ 2 kilogrammes. Le granit est à une distance moyenne de
24 cm de la fenêtre du détecteur, dont le diamètre
utile est estimé à 1,2 cm.
Avec des durées de comptage de 500 secondes, nous obtenons environ
130 évènements radioactifs, avec donc un écart-type
d'environ 11 : il est impossible de se prononcer.
Avec des durées de comptage de 2000 secondes, nous obtenons
: Sans granit, 582 évènements ; avec du granit 618, puis
613 évènements. Est-il possible de se prononcer ?
Prolongeons les mesures. Evaluons un ordre de grandeur : Supposons
que nous mesurions les évènements produits durant 10 heures
; nous pouvons nous attendre, en l'absence de granit, à environ
11000 évènements, avec un écart-type d'environ 105.
Le granit devrait produire environ 2 x 1000 x 3600 x 10, soit 72 millions
d'évènements radioactifs. On peut estimer que les rayonnements
et particules émises, pénétrant dans le détecteur,
seront d'environ 72 . 106 . p (0,006)2
/ (4 . p (0,24)2 . h)
, avec h rendement du détecteur, soit
11 250 . h. En prenant h
=
10% (Voir dans les données des valeurs plus réalistes), nous
devrions compter 11 000 + 1 125, soit 12 125 évènements,
à 110 près. Il semble possible de détecter la radioactivité
du granit.
// Note : p (0,006)2 est la surface d'entrée du détecteur ; (4 . p (0,24)2 . h), la surface de la sphère selon laquelle les rayonnements se répartissent.
Mesures effectives : Sans granit, départ du comptage à
13 h 16 min 0 s. Arrêt du comptage, le lendemain à 14 h 53
min 0 s. Nombre enregistré : 27 711.
Avec granit, départ du comptage à 14 h 53 min 0 s. Arrêt
du comptage, le lendemain à 12 h 06 min 0 s. Nombre enregistré
: 23 026.
Exploitez ces mesures. Que pouvez-vous en conclure ? Les informations
qui suivent vous permettent-elles de comprendre vos résultats ?
Données : Le rayonnement tellurique est dû aux nucléides suivants : 40K, U, Th et leurs descendants, notamment Ra. Ce rayonnement est essentiellement composé de rayons g (source : Notice du banc Crab, Jeulin). Le granit est riche en nucléides U et Th. Le radon 222Rn est émetteur a.
La notice du banc Crab, Jeulin, ne donne aucune indication sur les caractéristiques du détecteur Geiger-Müller employé. Le catalogue Leybold présente des détecteurs dont les caractéristiques semblent voisines :
Tube à compteur à fenêtre pour rayonnements
a,
b, g et X, référence 559 01 :
Compteur Geiger-Müller, dans boîtier en plastique, avec
fenêtre en mica très mince permettant aussi l'enregistrement
d'un faible rayonnement b. Livré
avec capuchon de protection pour la fenêtre en mica. Tension de travail
: 450 V. Largeur du palier : 200 V. Bruit de fond du palier : 0,2 impulsion
. s-1 environ (pour un blindage avec 50 mm de plomb et 3 mm
d'aluminium). Sensibilité au rayonnement g :
1% environ. Fenêtre de 9 mm de diamètre.
Tube à compteur à fenêtre pour rayonnements
b,
g, référence 559 00 :
Compteur Geiger-Müller, dans tube en verre.Tension de travail
: 550 V. Largeur du palier : > 250 V. Bruit de fond du palier : 0,5 impulsion
. s-1 environ (pour un blindage avec 50 mm de plomb et 3 mm
d'aluminium). Sensibilité au rayonnement g :
0,1% environ. Epaisseur de la paroi : Verre de 0,1 mm.
Réponse : Sans granit : 27711 évènements radioactifs (à + ou - 166), en 92220 secondes, soit une activité de 0,3005 Bq à + ou - 0,0018 Bq. Avec granit : 23026 évènements radioactifs (à + ou - 152), en 76380 secondes, soit une activité de 0,3015 Bq à + ou - 0,0020 Bq. Il semble que le granit soit plus radioactif que le milieu ambiant, mais il n'y a aucune certitude. Nous sommes à la limite de sensibilité et de bruit de fond du compteur Geiger-Müller
Vous trouverez sur ce site un logiciel libre que
j'ai écrit en Delphi, SimulRad. Il permet de simuler
une décroissance radioactive ; il est livré avec le texte
de ce travail pratique, qu'il est capable de lire et d'imprimer et il comporte
un extrait du code employé pour ses calculs :
Ce logiciel permet de simuler une décroissance radioactive, ou de tracer un histogramme - nombre d'évènements radioactifs détectés en une seconde, fréquence des différents nombres détectés.
Vous choisissez le nombre initial d’atomes radioactifs, supposés
identiques,
vous choisissez l’activité initiale,
vous choisissez la durée maximale de simulation.
A chaque boucle de calcul, supposée correspondre à une seconde, le logiciel teste tous les atomes restants et décide au hasard, ceux qui doivent se désintégrer.
Les limitations sont les suivantes :
1. Ordinateur rapide :Nombre d'atomes 200 000, durée 10 000
s ;
2. ordinateur lent :Nombre d'atomes 50 000, durée 3 000 s.
1 Lancez une simulation, en choisissant les paramètres
Nombre d’atomes initial 100, activité 2 Bq.
La courbe obtenue est-elle la représentation d’une fonction décroissante, monotone ?
Cette courbe est-elle la représentation (exacte, approchée ?) d’une fonction exponentielle ? Par quoi se traduit le caractère aléatoire des désintégrations ?
2 Lancez une simulation, en choisissant les paramètres :
Nombre d’atomes initial 100 000, activité 100 Bq.
La courbe peut-elle être considérée comme la représentation d’une fonction exponentielle ?
Pour répondre à cette question, vous pouvez Copier, puis
Coller les valeurs vers Excel (éventuellement, en ne gardant qu'un
point sur dix), tracer la courbe N = f(t), puis ajuster cette courbe par
une fonction exponentielle, en notant l’équation proposée
par Excel et le coefficient de régression.
Comparez les valeurs obtenues, à celles données par les
calculs du cours de physique.
// Note : Lorsque ce coefficient est proche de 1, ou -1, il est possible de dire que la fonction proposée ajuste convenablement les points portés sur le graphique.
// 2° Note : Si Excel ne vous propose pas la régression exponentielle (option grisée) dans le menu Courbe de tendance, c'est peut-être à cause d'un nombre excessif de points ; dans SimulRad, faites Copier 1 point sur 10.
// 3° Note : En éliminant les derniers points, lorsque le nombre de noyaux est faible et que nous ne sommes donc plus dans le domaine macroscopique, la régression donne de biens meilleurs résultats, correspondant au calcul du cours à quelques % près.
// 4° Note : Vous pouvez aussi, dans le logiciel SimulRad, zoomer sur la courbe tracée. Le zoom avant se fait par sélection d’un rectangle de gauche à droite ; le zoom arrière, par sélection de droite à gauche.
3 Observez le code des calculs réalisés par le logiciel.
Etes-vous d'accord avec la façon de calculer la probabilité
qu’a un atome de se désintégrer pendant un intervalle de
temps de une seconde. Cette probabilité est-elle toujours la même
au cours du temps ? L'activité de l'échantillon est-elle
toujours la même au cours du temps ?
Passez à la fenêtre histogramme. Vous pouvez choisir
l'activité espérée d'une collection d'atomes. Le nombre
de ces atomes est supposé constant au cours du temps.
Chaque seconde (en accéléré), le logiciel procède
à un tirage au sort des atomes qui se désintègrent.
Il enregistre leur nombre qui est représenté selon l'axe
des x. Ceci est effectué pendant 15 000 secondes. Selon l'axe des
y est représenté la fréquence à laquelle chaque
nombre d'évènements est apparu.
Effectuez quelques essais, pour différentes activités, puis répondez aux questions suivantes :
4 Comparez l'écart-type des résultats obtenus et leur moyenne.
5 Lorsque l'activité est faible, la répartition de l'histogramme (abstraction faite des fluctuations) est-elle symétrique ? Qu'en est-il lorsque l'activité est plus grande ?
6 Quelles sont les conditions à respecter dans une vraie expérience, pour que le nombre des atomes puisse être supposé constant au cours du temps.
Lire : Page 91, TP 1 : Lancer des dés ; page 93 : Stimulateur
cardiaque (exercice résolu) ; page 94 : Datation au carbone 14.
Pages 93 et suivantes, exercices :
16 (la représentation demandée, de la courbe de stabilité,
est une représentation très simplifiée), 17, 18, 20,
21, 24. Lire l'énoncé 28.
Note importante : Il se peut que votre
administrateur réseau ait configuré celui-ci de façon
restrictive, vous empêchant de lancer le logiciel de Physique Nucleus.exe.
Vous pouvez traiter directement avec lui, ou consulter sur ce site, les
pages réservées aux professeurs, accessibles par un mot de
passe. Vous y trouverez un logiciel et son mode d'emploi, permettant de
vous affranchir de cette restriction. Testez-le cependant préalablement
sur tous les postes. Dans notre lycée (réseau Win NT) cela
fonctionne.
Installation : Le logiciel Nucleus peut être complété par nucwav.exe, fourni dans nucwav.zip, qui ajoute des commentaires sonores sur les familles radioactives. Il suffit que les 2 exécutables soient décompressés dans le même dossier.
Pour l'installer, copiez dans un seul dossier à
votre convenance, les fichiers nucleus.zip et nucwav.zip, et décompressez-les
sur place à l'aide de WinZip. Un décompresseur téléchargeable
en même temps, nommé unzip.exe, vous rappellera le bon vieux
temps du DOS et de ses lignes de commande. Nous le déconseillons.
L'ensemble du dossier peut être déplacé
ou renommé. Créez une icône de raccourci sur le bureau,
pour l'exécutable Nucleus, uniquement
Si vous travaillez sur un poste du réseau du lycée,
faites une copie du dossier complet sur votre PC, dans un endroit raisonnable,
par exemple C : \ Program Files et placez un raccourci de l'exécutable
Nucleus.exe sur le bureau.
Compléments
d'information ![]() .
.
Possibilités : Nucleus.exe comporte dans
sa fenêtre d'accueil une carte complète de la vallée
de stabilité. Un clic souris sur un nucléide effectue
un zoom sur la carte. Il est alors pratique de se déplacer à
l'aide des touches fléchées. Vous voyez alors la durée
de demi-vie, la masse et les différentes désintégrations
possibles.
Un clic sur un nucléide affiche alors des propriétés
supplémentaires sur celui-ci.
Pour revenir en arrière, cliquez sur les boutons
Retour
ou Global, (ou Carte Globale).
Le bouton Filiations permet d'obtenir les familles
de nucléides : Cliquez sur Filiations, entrez au clavier le nom
du nucléide, par exemple 238u (sans espace) ou 238, puis 92. Si
le complément sonore a été placé dans le même
dossier que nucleus.exe, puis installé par Options | Son | Sound
Blaster | Retour, un commentaire sera lu. La touche Plus permet de faire
apparaître des variantes.
Le bouton Saut, suivi de 238u (sans espace) ou
238, puis 92, permet d'accéder directement au nucléide.
Paramétrage :
Petits problèmes :
Le bouton Options ne s'affiche pas toujours ; tapez
la lettre
O.
Le bouton Quitter n'apparaît pas en mode
Grand Public. Passez alors en mode Scientifique. Sinon, il faudra arrêter
en force, par Windows.
Si un être malfaisant (je parle des PC de notre
lycée, pas de ceux du Palais de la Découverte) a tout verrouillé
par un mot de passe, installez à nouveau le logiciel, à partir
du réseau : Faites une copie du dossier complet sur votre PC, en
écrasant l'ancien dossier.
Vous connaissez depuis longtemps la célèbre relation
qu'Einstein démontra en 1905
| E = m . c2 |
Cette relation d'apparence très simple signifie que de l'énergie
peut être transformée en masse, c'est à dire en matière,
et que de la masse peut disparaître en donnant de l'énergie.
Bien sur cela ne se produit de manière mesurable que dans des circonstances
particulières. Nous avons vu par exemple le cas de l'annihilation
des électrons et des positons.
Lors des transformations chimiques, les énergies mises en jeu
sont si faibles que la masse ne change pas, d'où les équations
bilan.
Considérons la désintégration du radium :
|
|
|
|
|
Cette réaction nucléaire libère donc de l'énergie cinétique et de rayonnement. Cette énergie ne peut provenir que d'une diminution de la masse au cours de la réaction. Vérifions cela ; nous ne nous occuperons pas des cortèges électroniques.
Nous trouvons la masse du noyau de radium, à partir de la base de données du logiciel nucleus.exe. Pour cela, il faut faire trois choses :
La perte de masse est de : 225,977 13 - 221,970 04 - 4,001 50 = 5,59
. 10-3 u.
Elle correspond à une énergie de : 5,59 . 10-3
x 1,66 . 10-27 x (3 . 108)2 = 8,4 . 10-13
J, soit encore 5,2 MeV.
Dans toute réaction nucléaire spontanée, il y a perte de masse.
// Remarquez qu'il faut beaucoup de chiffres significatifs, au début des calculs, et que la précision diminue, à cause de la soustraction. Pensez, à la fin de vos calculs, à garder un nombre raisonnable de chiffres significatifs (2 ou 3).
L'énergie dégagée par une réaction nucléaire
paraît très faible, mais n'oubliez-pas qu'il s'agit de l'énergie
produite par un seul noyau.
Les physiciens préfèrent, lorsqu'ils travaillent à
l'échelle nucléaire, exprimer l'énergie en électronvolt
(symbole eV).
L'électronvolt est le produit de la charge élémentaire,
valeur absolue de la charge de l'électron, par l'unité de
tension, le volt.
Montrons qu'il s'agit bien d'une énergie :
[eV] = C . V ; or C = A . s ; donc l'électronvolt se mesure en
A . s . V ou A . V . s, soit W . s, soit des joules.
1 eV = 1,6 . 10-19 x 1 = 1,6 . 10-19
J.
Une unité de masse atomique correspond à :
1,66 . 10-27 x (3 . 108)2 = 1,49 .
10-10 J = 0,9 . 109 = 930 MeV.
Si on forme un noyau (on peut au moins imaginer qu'on le fasse),
à partir de ses nucléons,
Nous avons vu que la masse de ce noyau est de 225,977 13 u.
La masse des nucléons qui le forment est : 88 x 1,007 270 0
+ (226 - 88) x 1,008 665 8 = 226,826 97 u ;
Le défaut de masse du radium 226Ra est 226,826
97 - 225,977 13 = 0,849 u.
Soit une énergie de liaison de 0,849 x 930 MeV ou encore 790
MeV.
Plus l'énergie de liaison est grande, plus le noyau se trouve
dans un puits de potentiel profond ; mais ce qui importe, c'est le quotient
de cette énergie de liaison par le nombre de nucléons. La
courbe
d'Aston représente l'opposée de l'énergie de liaison,
rapportée à un nucléon, El
/ A.
Pour l'élément uranium, les différents isotopes
donnent quasiment un même point sur la courbe d'Aston. Exemple El
/ A = 7,64 MeV pour l'uranium 218 et 7,53 MeV pour l'uranium 242, soit
1 % de variation. Il y a plus de différence pour les isotopes du
fer et encore plus pour ceux de l'hydrogène :
| Isotope | 1H | 2H | 3H | 4H | 5H | 6H |
| El / A en MeV | 0,006 | 1,110 | 2,826 | 1,392 | 0,548 | 0,964 |
Un noyau est d'autant plus stable que son énergie de liaison par nucléon est grande (il s'agit bien de la valeur absolue, positive).

Exercice : A partir de ce qui vient d'être dit quant au défaut de masse et à son origine, critiquez la méthode consistant à soustraire de la masse de l'atome, celle des électrons, pour obtenir la masse du noyau. Pour quelle raison cette méthode donne-t-elle cependant des résultats très satisfaisants ?
Imaginons qu'un noyau d'uranium 235 se désintègre
spontanément, jusqu'à donner l'isotope stable de sa famille,
soit le plomb 207. Au cours de la série de réactions nucléaires,
il se forme 7 noyaux d'hélium 4 (rayonnement a),
et 4 électrons (rayonnement
b-).
La masse d'un noyau d'uranium 235 est de 235,043930 - 92 x 0,00055 =
234,99333 u.
La masse d'un noyau de plomb est de 206,975876 - 82 x 0,00055 = 206,930776
u.
La masse d'un noyau d'hélium est de 4,002603 - 2 x 0,00055 =
4,001503 u.
La masse finale totale est donc : 206,930776 + 7 x 4,001503 + 4 x 0,00055
soit 234,943497 u.
La perte de masse est : 234,99333 - 234,943497 = 0,049833 u arrondi à 0,0498 u.
Soit 0,0498 x 1,66 . 10-27 = 8,27 x 10-29 kg ;
soit donc 8,27 x 10-29 x (3 . 108)2 =
7,4 . 10-12 J pour un noyau d'uranium, soit encore de 4,5 .
1012 J pour une mole ou 235 g d'uranium.
Cela correspond à l'énergie produite par la combustion
de 160 tonnes de charbon, qui produirait 300 000 mètres cubes de
dioxyde de carbone, en consommant aussi 300 000 mètres cube de dioxygène.
Le défaut de masse total d'un noyau 207Pb
est de 1,748 u, soit 7,868 MeV par nucléon. Le défaut de
masse total d'un noyau 235U est de 1,9145 u, soit 7,589 MeV
par nucléon.
Si le noyau d'uranium 235 se désintègre
de manière provoquée, jusqu'à donner des noyaux plus
légers, se situant au minimum de la courbe d'Aston (- 8,7 MeV par
nucléon), il se libérera 8,7 - 7,589 = 1,1 MeV par nucléon,
soit pour 235 g d'uranium 235 :
1,1 . 106 x 235 x 1,6 ; 10-19 x 6,02 ; 1023 = 2,5 . 1013 J.
Mais dans l'exemple précédent, suite de réactions
nucléaires spontanées, se pose un problème de
taille : La demi-vie de l'uranium 235 est de 704 millions d'année.
Il est grandement nécessaire d'accélérer la désintégration.
Pour cela, des neutrons sont projetés sur l'uranium qui éclate
en deux autres noyaux, c'est une réaction nucléaire provoquée
appelée fission.
|
+ |
|
|
|
|
|
+ 3 |
|
+ | g |
m (U) + m (n) - m(Sr) - m (Xe) - 3 . m (n) = 234,993 35 - 93,894 51
- 138,889 17 - 2 x 1,008 67 =
0,192 33 u, arrondi à 0,192 u, soit 0,192 x 932 = 179 MeV.
1 mole d'uranium 235, soit 235 grammes, libérera :
179 . 106 x 1,6 ; 10-19 x 6,02 ; 1023
= 1,7 . 1013 J.
C'est l'énergie libérée par la combustion de 600
tonnes de charbon dans 1,2 millions de mètres cubes de dioxygène,
dégageant 1,2 millions de mètres cubes de dioxyde de carbone.
La fission est réalisée dans les réacteurs nucléaires pour produire de l'énergie et dans la bombe A, démonstration éclatante de l'adage :" Science sans conscience n'est que ruine de l'âme".
La courbe d'Aston montre que si on part d'éléments
très légers, isotopes de l'hydrogène, pour former
des noyaux plus lourds, la perte de masse par nucléon est beaucoup
plus importante, donc la libération d'énergie bien plus grande.
Dans le Soleil et les étoiles a lieu la réaction de fusion de l'hydrogène, première étape de la formation de l'hélium, puis des autres éléments (nous sommes nous-mêmes constitués de carbone, d'oxygène... qui ne peuvent provenir que de l'explosion d'une étoile en fin de vie. Le Soleil est donc une étoile de deuxième génération).
|
+ |
|
|
|
|
|
Ce qui fait, pour 2 grammes d'hydrogène,
4,6 . 10-4 x 932 . 106 x 1,6 ; 10-19
x 6,02 ; 1023 = 4,1 . 1010 J.
Voici deux réactions, partant du deutérium et du tritium, que les scientifiques cherchent à maîtriser, pour la production d'énergie :
|
+ |
|
|
|
|
|
|
+ |
|
|
|
|
|
Cette réaction de fusion nécessite un confinement
de la matière à très haute température et très
haute pression. C'est ce qui est réalisé dans la bombe H,
preuve évidente que l'Homme se rapproche de Dieu, sauf en sagesse.
Les états possesseurs de la bombe H, malgré les progrès
du désarmement nucléaire, possèdent de quoi faire
sauter au moins 100 fois notre planète. Les militaires ont une très
belle expression pour résumer l'effet de telles bombes sur un pays
: La vitrification, c'est à dire la fusion du sol et de tout ce
qui est dessus sur une épaisseur de près d'un mètre,
et cela à l'échelle de la France.
Bien plus intéressante, mais considérablement plus difficile,
est la maîtrise de la fusion à des fins de production d'énergie.
Pour cela, les Américains privilégient un confinement
laser ; les Européens et les Japonais travaillent sur une technique
Russe, le confinement magnétique dans un Tokamak (tore magnétique,
en russe). Les Européens sont ainsi déjà parvenus
à une fusion contrôlée mais de gros problèmes
de récupération de l'énergie émise se posent.
// Note : Ce travail pratique sera amélioré et
des éléments de réponse aux questions posées
seront ajoutés, dès que nous aurons pu, par nous-mêmes,
faire des mesures convaincantes d'activité du sol ; malheureusement,
la firme Leybold ne propose plus son détecteur ultra sensible de
radioactivité qu'elle a remplacé par un détecteur
à compteur Geiger classique, mais de poche, programmable, autonome
et permettant d'enregistrer, puis de transférer sur ordinateur ses
mesures. Ce détecteur est aussi fourni par Conrad électronique
à un prix intéressant.
Objectifs : Vous allez dans un premier temps noter en quelques lignes vos premières impressions à le lecture de la série d'articles parus dans la presse locale et concernant la radioactivité dans notre région, puis vous allez (essayer de) passer ces déclarations au crible de l'analyse scientifique. Vous devrez rechercher dans le logiciel Nubase le comportement des nucléides cités dans les articles et faire le tri entre déclarations émotionnelles, analyses scientifiques et charlatanisme.
Extraits d'une série d'articles publiés dans le mensuel "La Presse Pontissalienne", n° 35, Septembre 2002.
// Note : Seuls des extraits, aussi objectifs
que possible, des différents articles figurent ici. Nous avons mis
en caractères gras les informations que les journalistes
ont voulu faire eux-mêmes ressortir. Les informations que nous avons
ajoutées sont en bleu.
| La Presse Pontissalienne, première page : Tchernobyl : enfin la vérité sur notre région. Lire en p. 7 à 10. |
| Page 7 : Dossier : Tchernobyl : enfin la
vérité
Texte de la rédaction de La Presse Pontissalienne : Le 26 Avril 1986, le réacteur 4 de la centrale de Tchernobyl explose dégageant dans l'atmosphère une forte quantité de débris radioactifs. On connaît la suite. De l'hallucinant mensonge de l'État qui affirmait à l'époque que le nuage s'était arrêté à nos frontières, aux relevés de terrain effectués en 2001 par la C.R.I.I.R.A.D. qui a mis en avant l'importance de la contamination... A plus de 2000 km de l'Ukraine, le Haut-Doubs, comme l'ensemble du grand est de la France est plus que jamais concerné par cette question même si aujourd'hui les spécialistes s'accordent à dire que les effets s'amenuisent. On mesure encore jusqu'à 15 000 Bq/m2 dans certains secteurs de cette zone géographique. Faut-il s'en inquiéter ? Pour la première fois en France, un collectif de médecins franc-comtois a mené une vaste enquête épidémiologique sur la région afin d'apporter les premiers éléments de réponse à cette question... |
| Rappel des faits Aucune mesure de prévention...
L'article
expose les mesures prises par les pays voisins de la France (Luxembourg,
Allemagne, Italie), laver soigneusement les légumes frais, interdiction
des légumes à feuille et du lait au enfants de moins de 12
ans, voire interdiction totale des légumes frais...
A Besançon, le laboratoire de micro-analyse nucléaire de la faculté des sciences venait d'installer de nouveaux appareils de mesure. "Nous avons constaté une augmentation de la radioactivité ambiante, se souvient Didier Klein, professeur des universités. Nous avons téléphoné à la préfecture pour les prévenir mais ils nous ont répondu qu'ils n'étaient pas bien au courant donc n'ont pas réagi. Tout simplement parce que l'État n'a donné aucune directive". Dans le Doubs comme ailleurs, aucune autorité officielle n'a eu la moindre réaction de mise en garde de la population, suivant les instructions d'un gouvernement qui a selon toute vraisemblance, nourri un mensonge permanent. C'est bien là tout l'enjeu de la plainte déposée le 1er mars 2001 par l'association des malades de la thyroïde qui souhaite voir reconnues les carences graves des autorités de l'époque... |
| Page 8 Réaction Dénoncer un mensonge d'État |
| Roland Desbordes : "Les victimes sont en droit
de demander des comptes à l'État"
Le président de la C.R.I.I.R.A.D. revient sur 16 ans de mutisme de l'État français. La Presse Pontissalienne : Le 1er mars 2001, la C.R.I.I.R.A.D. a déposé une plainte contre X, avec l'association des malades de la thyroïde. Aujourd'hui où en est le dossier ? Roland Desbordes : Il est en cours d'instruction... le gouvernement de l'époque était totalement au courant... Il a menti volontairement afin d'éviter que soit remise en cause l'industrie nucléaire... Je veux que l'on reconnaisse qu'il y a eu mensonge d'État. L.P.P. : Vous avez publié un atlas des contaminations radioactives au niveau national. Il apporte des résultats significatifs. Sur la base de ce document, que peuvent attendre les malades qui ont déposé plainte aux côtés de la C.R.I.I.R.A.D. ? Roland Desbordes : A partir des données de ce document, on peut prouver qu'on n'a pas fait ce qu'il fallait... Nous on estime qu'avec les valeurs que l'on avance, on peut démontrer que Tchernobyl a forcément eu un impact sanitaire. Ainsi les victimes d'un cancer de la thyroïde sont en droit de demander des comptes à l'État. Il est bien évident qu'on ne pourra jamais prouver que cette maladie est due à 100% à Tchernobyl. c'est pourquoi j'aimerais qu'on reconnaisse en France le principe de présomption qui a été adopté aux U.S.A. après la guerre du Golfe. Il admet que l'on puisse être victime de pollutions. A partir de là, j'estime que la justice peut dire qu'il y a une relation entre le cancer de la thyroïde et Tchernobyl... L.P.P. : Vous soutenez que le nombre de pathologies de la thyroïde a tendance à augmenter. Pourtant rien ne permet véritablement de le prouver ? Roland Desbordes : En effet, nous ne disposons d'aucune donnée au niveau national. Il n'y a que des initiatives individuelles comme celle du Professeur Viel que je salue... L.P.P. : Est-ce qu'un jour toute la lumière sera faite sur cette affaire ? Roland Desbordes : Actuellement, 415 malades de la thyroïde se sont associés à la plainte... Propos recueillis par T.C. |
| Page 8 Étude 8 cancers de la thyroïde
en 19 ans
L'effet Tchernobyl n'est pas affirmé Les résultats d'une étude unique menée en Franche-Comté, sur les enfants de moins de 15 ans dévoilent que l'augmentation des cancers de la thyroïde n'est pas significative pour parler d'un effet Tchernobyl. "Il se dit depuis 20 ans que les cancers de la thyroïde sont en progression. Est-ce que cette augmentation est due à Tchernobyl ? On ne peut pas l'affirmer. Là est notre grande difficulté" admet le professeur Jean-François Viel, épidémiologiste au C.H.U. de Besançon. c'est lui qui avec le docteur Frédéric Mauny, ont été l'investigateur d'une étude exemplaire commanditée par la section généraliste de l'union régionale des médecins libéraux de Franche-Comté. L'objet ; "Estimer l'incidence des cancers de la thyroïde dans la région, à la recherche d'une éventuelle augmentation à partir de 1986." Et voici le point de départ de la première étude scientifique pilotée à l'échelle de la Franche-Comté dans le but d'évaluer les conséquences sanitaires possibles du nuage de Tchernobyl chez les moins de 15 ans (cf : les enfants, public à risque). Une première en France dont les promoteurs ont été les généralistes qui semblaient constater parmi leur clientèle pédiatrique un nombre croissant de pathologies thyroïdiennes... Après 4 ans d'investigation, les premiers résultats de l'étude ont été divulgués en 2001 pour deux pathologies : le cancer de la thyroïde et le diabète insulino-dépendant. Pour la troisième relative aux hypothyroïdies, les résultats sont en cours de validation. Il en ressort que le lien entre ces maladies et le dépôt radioactif n'est pas confirmé. "Nous avons travaillé sur la durée de 1980 à 1999 en essayant de mettre en évidence une augmentation après 1986. Pour cela nous nous sommes concentrés sur deux périodes : Tout d'abord 1980-1989, et non 1986, considérant qu'il y a un temps de latence avant l'apparition de la maladie. Ensuite 1990-1999, période dite à risque d'avoir un cancer. Résultat, après enquête auprès des spécialistes, des hôpitaux etc, nous avons recensé 8 cas de cancer de la thyroïde sur toute la Franche-Comté" poursuit le Pr Viel. 8 cas en 19 ans chez les enfants de moins de 15 ans, dont 3 entre 1980 et 1989 et 5 sur la seconde période (pour le Doubs 3 cas ont été répertoriés en 19 ans). Conclusion : "Nous ne mettons pas en évidence de variation significative du cancer de la thyroïde de l'enfant, ni dans le temps, ni dans l'espace". Et d'ajouter : "On ne peut donc pas conclure à une relation de cause à effet". Mais le diagnostic est serré... ... pour le diabète insulino-dépendant... "Là on a recensé 295 enfants chez qui on a diagnostiqué la maladie entre 1980 et 1999. Cela pouvait être lié à Tchernobyl. Pour le coup cela représentait une augmentation significative de 4,7 % par ans entre les deux périodes". La progression est constatée sur les quatre départements. Alors dans le souci d'une démarche scientifique rigoureuse, les chercheurs ont établi une comparaison avec les données nationales et européennes. "On s'est aperçu que la progression est égale à celle que l'on rencontre dans d'autres pays". Conclusion, cette fois encore l'effet Tchernobyl est écarté. "Les grandes hypothèses sont notamment l'hérédité et l'obésité"... |
| Page 9 Justice Lever le voile sur Tchernobyl
Les malades veulent connaître la vérité L'association française des malades de la thyroïde a déposé une plainte contre X pour qu'une étude épidémiologique soit engagée en France. ... "Cette affaire doit être éclaircie. Le problème est qu'il y a 40 tonnes de dossiers à éplucher, il faudra des années" lance Chantal Garnier, co-présidente de l'association... derrière ses mots, il y a l'attente des malades de la thyroïde. Ils sont plus de 2200 aujourd'hui à avoir rejoint l'association créée en 1999... "Nous avons de plus en plus de jeunes, beaucoup d'enfants"... "Nous connaissons des familles entières dans lesquelles les parents et les enfants ont une pathologie de la thyroïde et ce n'est pas héréditaire."..."... on rencontre des jeunes qui n'ont pas de travail, qui ne peuvent pas faire de prêt à la banque parce qu'ils ont un cancer. Avant Tchernobyl, il y en avait peu. Actuellement, ils sont de plus en plus nombreux. Nous prévoyons un pic aux environs de 2005." |
| Page 9 Réaction Pas d'effet de seuil
Franco Pierangelo : "Nous sommes dans une zone de doute" Médecin généraliste à Arc-sous-Cicon, il fait partie de l'union régionale des médecins libéraux qui a demandé et financé l'enquête épidémiologique en Franche-Comté. Commentaire d'un homme de terrain. La presse Pontissalienne : cette étude serait justifiée par une augmentation des cancers de la thyroïde constatée par les généralistes ? Franco Pierangelo : Non, le point de départ de cette étude n'est pas une constatation, mais une appréhension... L.P.P. : Avez-vous décelé de nombreux cas de cancer de la thyroïde ? Franco Pierangelo : Nous sommes devant des pathologies assez rares... L.P.P. : Quel discours tenez-vous auprès de vos patients ? Franco Pierangelo : J'essaie d'être rassurant... Le risque est derrière nous. Il était présent dans les jours qui ont suivi la catastrophe au moment où l'on trouvait l'iode 131, un élément radioactif dangereux dont la demi durée de vie est de 8 jours... |
| Page 10 Radioactivité Contamination
des sols au césium 137
9 800 Bq/m2 relevés à Levier en 2001 La C.R.I.I.R.A.D. a publié un ouvrage dans lequel elle a regroupé l'ensemble des mesures qu'elle a effectué sur le terrain... 15 ans après la catastrophe de Tchernobyl. Plus de 3000 relevés... donnent un aperçu global de la contamination actuelle des sols au césium 137... elle évolue de 5100 à13800 Bq/m2... "On estime que cette mesure récente correspond aux 2/3 du césium déposé en 1986." La demi-vie du césium 137 est de 30 ans. "Le césium 137 se situe maintenant entre 10 et 20 cm dans le sol. Le danger est écarté sauf peut-être pour les grands consommateurs de champignons et de sangliers..." L'article est illustré par une photographie montrant 3 membres de la C.R.I.I.R.A.D., portant casque et bottes, pointant 2 compteurs Geiger vers le sol (1 au contact, l'autre à 75 cm), sur une crête parsemée de blocs (de granit ?). |
| Page 10 Consommation Peu de risques localement
Vigilance avec les champignons des pays de l'est "Au moment du passage du nuage de Tchernobyl, il a été mesuré localement des taux de 400 Bq / kg sur des champignons frais. Maintenant l'activité moyenne mesurée est de 70 Bq / kg. On est désormais bien en-dessous de la dose maximale tolérée au niveau européen qui est de 600 Bq / kg" explique Jean-Marc Moingeon, de la société d'histoire naturelle du Haut-Doubs... "En plus le césium est un élément assez lourd qui aurait tendance à s'enfoncer et à se situer désormais hors de portée du mycélium." |
Quelques indications, pour guider votre recherche
Quelles sont les unités qu'il faut employer pour mesurer la
radioactivité d'un échantillon ?
Quelle est l'activité
Recherches documentaires, sur l'histoire de la fission et de la
fusion ; sur la gestion des déchets.
Lire : Page 112 : Réactions stellaires ; page 113
: Réactions de fission.
Exercice : Calculez l'énergie qui est libérée
dans la réaction nucléaire de fusion, deutérium, tritium.
Pages 114 et suivantes, exercices n° : 23, 25, 18.
Nos élèves ont parfois du mal à
régler leurs oscilloscopes, mais font preuve curieusement de beaucoup
de talent pour les dérégler et les placer dans des modes
exotiques.
En dehors de l'affichage en japonais, l'un des plus graves
désagréments se produit lorsque le déclenchement
de l'oscilloscope se produit trop tôt (ou trop tard), c'est à
dire lorsque la partie intéressante de la courbe est "tracée"
à gauche de l'écran, lequel ne montre plus que la fin sans
intérêt de la courbe. Par exemple, une charge de condensateur
donne désespérément un segment d'horizontale. Ce problème
se détecte au fait que la flêche supérieure indiquant
l'instant du déclenchement se trouve en butée, au bord de
l'écran. Ramenez-la vers le milieu, à l'aide du bouton de
déplacement horizontal. Si plusieurs tours de celui-ci ne suffisent
pas, passez à une vitesse de balayage moins rapide et recommencez.
Un autre problème est l'apparition d'artefacts
dus à la numérisation (sous-échantillonnage).
Il peut se produire lors de l'utilisation des émetteurs à
ultrasons en mode salve. Consultez sur ce site le cours de M.P.I. consacré
à l'échantillonnage. Montrez aux élèves ce
qui se passe lorsqu'on diminue la vitesse de balayage, donc d'échantillonnage.
Au lieu d'une fréquence de 40 kHz, on pourrait trouver une fréquence
aberrante de 3 Hz.
Retour au texte précédent, évolution temporelle des systèmes, étude d'une simulation d'ondes sismiques