Sommaire : Relativité du mouvement, référentiel,
les effets d'une force, le principe de l'inertie, travail pratique.
Le mouvement d'un objet est relatif à un référentiel.
Tout solide lié à la Terre est un référentiel
terrestre.
Dans un référentiel donné, un point est en
mouvement si sa position varie au cours du temps.
Position <-> coordonnées dans un repère ;
temps (ou date) donné par un chronomètre.
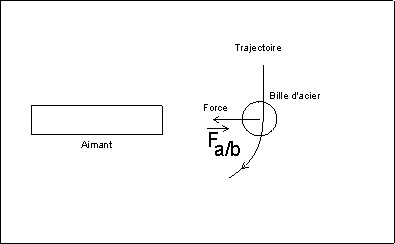
La trajectoire d'un point mobile est l'ensemble des positions qu'il occupe au cours du temps. La trajectoire dépend du référentiel.

Une force qui s'exerce sur un corps peut mettre ce corps en mouvement, modifier sa trajectoire, modifier sa vitesse.
Si un corps n'est soumis à aucune force, ou à
des forces qui se compensent,
s'il était en mouvement, ce mouvement est rectiligne et uniforme. |
Remarque : Ce principe est vrai dans des référentiels particuliers, appelés galiléens. Par exemple, le référentiel terrestre. Citons un contre exemple évoqué par le savant russe Landau dans un de ses livres de vulgarisation de la physique : Vous avez pris place à bord d'un navire pour une croisière. Le navire est à quai, vous vous installez dans votre cabine (sans hublot). Le lustre de la cabine pend au bout de son câble, tout est normal. Vous vous endormez. A votre réveil, le lustre se balance. Qu'en concluez-vous ? Qu'un lustre soumis à des forces qui se compensent est obligatoirement animé d'un mouvement de balancement ? Ou que votre référentiel, le bateau, n'a plus ses propriétés initiales ? La réponse est ici évidente.
Pages 240 et suivantes, exercices n° 10, 11, 13, 15, 23.
Ce document comporte une présentation, un questionnaire assez
long qui pourrait faire l'objet de deux séances de travaux pratiques
et les réponses.
Ordinateur, enregistrement vélo.avi
disponible sur ce site (ou tout autre équivalent, par exemple velchu.avi,
mais vous constaterez que vélo.avi est plus net et lisible - à
vous de voir si je me vante), logiciel d'exploitation des fichiers .avi
(WinLabo2 ou Synchronie, ou plus simplement LireAvi,
graticiel ultra simple d'emploi, disponible sur ce site ou AviMeca
graticiel proposé par un collègue brestois, Alain Le Gall,
offrant plus de possibilités et donc un peu plus complexe à
utiliser), Excel ou tout autre tableur, imprimante.
Pour le cas où la salle informatique ne serait
pas disponible, il est intéressant d'imprimer les images successives
du film avi, en couleur de préférence, et d'en réaliser
des photocopies placées sous jaquette plastique, ou plastifiées.
Dans le dossier contenant velchu figurent les mêmes images, sous
forme de bitmaps, de meilleure qualité donc. Vous pourriez marquer
en rouge la balle et l'axe du pédalier, pas toujours très
visibles.
Un cycliste, qui roule à vitesse constante, lâche à
l'instant 0,16 s (environ) une balle. Il est filmé par une caméra
fixe qui enregistre 25 images par seconde.
A quel endroit la balle doit elle heurter le sol ? (Répondre
d'abord avant d'avoir vu les images).
Lancez WinLabo2 et créez une nouvelle feuille de calcul.
Par Fichier | Importer AVI, chargez le fichier velchu.avi.
Réglez les échelles horizontales et verticales, en déplaçant
à la souris les pointeurs marquant 1 mètre.
Faites passer les images une par une et transférez les coordonnées
du centre de la balle dans la feuille de calcul, par un clic droit. Les
colonnes contiennent x, y et t, dans cet ordre.
Attention ! WinLabo2 'plante' souvent. Sauvegardez vos résultats.
Tracez la trajectoire de la balle dans le référentiel terrestre.
En quel point particulier, la balle frappe-t-elle le sol ?
A quoi cela est-il dû ?
(La réponse à cette question permet de faire resurgir tout ce qui traîne de mécanique pré galiléenne dans la tête des élèves).
Tracez la trajectoire de la balle dans le référentiel lié au cycliste.
Quelle est cette trajectoire, à quoi cela est-il dû ? Cela confirme-t-il les conclusions précédentes ?
Pour cela, transférez par copier coller les résultats
précédents dans Excel. Sauvegardez.
Revenez dans WinLabo2 et effacez ces résultats, puis trouvez
les coordonnées successives de l'axe du pédalier dans le
référentiel terrestre. Transférez les dans Excel.
Par soustraction, trouvez les coordonnées successives de la
balle dans le référentiel lié au cycliste. Tracez
la trajectoire à l'aide d'Excel.
Les fluctuations observées sont-elles importantes ? Evaluez leur amplitude. Quelle est leur cause probable ?
Observez le mouvement de la balle après qu'elle ait touché le sol. A quoi est-il dû ?
Prouvez que la caméra est fixe par rapport au référentiel
terrestre.
Prouvez que le cycliste roule à vitesse constante.
Les cinéastes qui ont enregistré velchu.avi n'ont pas
placé de règle verticale de 1 mètre. Comment placer
avec précision l'index vertical 1 mètre ?
La balle frappe le sol à l'endroit où se trouve au
même instant le cycliste.
Pour obtenir une trajectoire, il faut tracer y en fonction de x (t
n'intervient pas).
La première réponse correspond au fait suivant : Dans
son mouvement horizontal, la balle n'est soumise à aucune force
(on suppose, sans insister, que le mouvement peut s'étudier indépendamment
selon les deux axes de coordonnées). Son mouvement est donc uniforme,
c'est le principe de l'inertie. Elle avance donc à la vitesse constante
du cycliste. L'influence des frottements dus à l'air pourra être
étudiée dans la question suivante.
Dans le référentiel lié au cycliste, la balle a
une trajectoire verticale. Elle va de plus en plus vite sous l'effet de
son poids lui aussi vertical.
Les fluctuations sont faibles, de quelques centimètres, dues
vraisemblablement à l'imprécision de l'enregistrement et
du pointage. On n'observe pas de décalage dû au frottement
de la balle dans l'air.
La balle part en arrière (par rapport au cycliste) après
avoir touché le sol ; c'est dû aux frottements sur le sol.
La caméra est fixe si le paysage ne défile pas.
Il faut étudier le mouvement de l'axe du pédalier ; il
doit être régulier (points équidistants).
Il y a un problème lié au réglage de l'écran.
Repérer le diamètre de la roue (et pour le professeur mesurer
g !)
Sommaire : Comment décrire le mouvement
de la Lune ? l'interaction gravitationnelle, poids et force gravitationnelle,
pourquoi la Lune ne tombe-t-elle pas ? travail pratique.
Le référentiel terrestre n'est pas adapté pour
l'étude du mouvement de la Lune.
Le référentiel géocentrique a pour origine le centre de la Terre et des axes pointant vers des étoiles fixes.
Dans ce référentiel, la Lune décrit un cercle de rayon 384000 km en 27,3 jours (période sidérale).
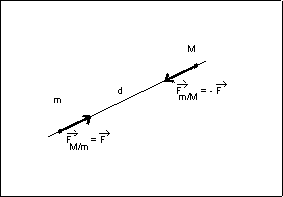
Deux corps ponctuels, de masses m et m', séparés par une distance d, exercent l'un sur l'autre des forces attractives de valeur :
F = G . m . m' / d 2
G est la constante de gravitation universelle, G = 6,67 ; 10 -11 m 3 . kg -1 . s 2.
F s'exprime en newtons, m et m' en kilogrammes, d en mètres.
Ce résultat se généralise aux corps à répartition sphérique de masse (masse régulièrement répartie autour du centre), en mesurant la distance d, de centre à centre.
// Vous trouverez sur ce site, dans le chapitre Olympiades de la Physique, un montage de mesure de la constante de gravitation universelle. Notez que cette constante pose problème aux physiciens ; lors de sa définition la plus récente (1998), la précision a été diminuée, ramenée à trois chiffres significatifs, ce qui est ignoré de certains (nombreux) ouvrages scolaires, dans leur page de garde sur les constantes physiques.
Le poids d'un corps est pratiquement égal à la force
de gravitation exercée par la Terre sur ce corps.
Exercice : MT = 5,98 . 10 24 kg, RT = 6380 km. Calculez la force de gravitation exercée par la Terre sur une masse m de 1 kg.
Parce qu'elle possède une vitesse lui permettant d'être
satellisée.
// Cet exercice sera l'occasion pour le professeur de découvrir
qu'au delà des mots, un fort pourcentage d'élèves
confond
encore force et vitesse, c'est à dire en est resté à
la physique aristotélicienne (c'est encore le cas de pas mal d'élèves
en début de terminale S). Pauvre Galilée. Cela ne valait
pas la peine qu'il risquât le bûcher.
Est-il soumis à une force, à aucune force, à
deux forces qui se compensent ?
Pages 253 et suivantes, exercices n° 11 (ajouter : calculer
la valeur de la force gravitationnelle exercée par la Lune sur la
Terre, avec : masse de la Lune, ML = 7,34 . 1022
kg et distance Terre - Lune = 384000 km), 16, 17, 19, 23.
Consultez le chapitre TP, IESP, MPI. vous y trouverez un logiciel
gratuit réalisé par l'auteur de ce site, permettant de tracer
les trajectoires de satellites au voisinage des planètes du système
solaire et du Soleil. Il emploie la méthode d'Euler. Plusieurs sujets
de TP sont inclus dans le logiciel.
Sa dernière version, 5.0.0, permet maintenant (à partir
du premier Aout 2001) les transferts de données dans Excel.
Vous trouverez sur ce site la méthode permettant de superposer
2 courbes dans Excel. Pour transférer les données
(date, coordonnées du satellite et coordonnées du point
de la surface de la terre à sa verticale) faites Edition | Copier.
Dans Excel, cliquez dans la première cellule en haut à
gauche, puis faites : Edition | Collage spécial | Coller avec liaison
et En tant que Text. Chaque modification de trajectoire de satellite
sera automatiquement répercutée sur votre
graphique dans Excel. Il vous restera à choisir les échelles
pour que la Terre soit ronde !
Une fusée largue à l'altitude de 3,59 . 107
m une sonde spatiale. Trouvez par essais successifs dans le logiciel de
simulation, la direction et la vitesse de la fusée au moment où
elle se sépare de la sonde, pour que celle-ci décrive autour
de la Terre une trajectoire circulaire.
Quelle est alors la durée d'un tour de la Terre par le satellite
?
Si vous ne voyez pas l'astre attracteur, c'est peut être parce qu'il est trop petit, donc que vous en êtes trop loin.
Sommaire : Phénomène périodique,
l'alternance des jours et des nuits, l'alternance des phases de la Lune,
l'alternance des saisons, travail pratique, activité documentaire
: les calendriers, travail pratique, activité documentaire : le
calendrier cosmique.
C'est un phénomène qui se reproduit identique à
lui-même, à intervalles de temps réguliers.
Plan méridien d'un lieu : Plan passant par les pôles
et contenant la verticale de ce lieu.
La période de passage du Soleil dans le plan méridien est de 24 heures ; c'est le jour solaire moyen.
1 heure = 60 minutes (symbole min),
1 minute = 60 secondes.
Ce système de numération remonte aux Babyloniens.
Ce mouvement apparent du Soleil est dû à la rotation propre de la Terre.
Exercice : Trouvez les diviseurs entiers des nombres 60 et 3600. Comprenez-vous pourquoi ce système de numération sexagésimal a été conservé depuis plusieurs millénaires ?
Successivement, on peut observer le premier quartier ( p ), la pleine
lune ( O ), le dernier quartier ( d ) et la nouvelle lune ( ). Cela
résulte de la rotation du centre de la Lune autour du centre de
la Terre. La période de ce phénomène, appelée
lunaison, vaut 29 j 12 h 44 min.
Au cours d'une année, par deux fois, le jour et la nuit ont
une durée égale ; ce sont les équinoxes.
La Terre fait un tour du Soleil, dans le plan de l'écliptique,
en une année tropique (durée séparant deux équinoxes
de printemps), soit 365,2422 jours. L'alternance des saisons provient de
ce que l'axe des pôles de la terre garde une direction fixe, mais
qui fait un angle de 23 ° 27 ' avec la normale au plan de l'écliptique.
Notre calendrier, dit grégorien, est basé sur l'année
tropique.
Pages 269 et suivantes, exercices n° 15, 19, 32.
La durée moyenne d'une lunaison est de 29,5306 jours ; celle
de l'année tropique de 365,2422 jours.
Lorsque Jules César arrive au pouvoir, en 49 avant J.C., l'année romaine vaut 366,6 jours. En 46 avant J.C. Jules César consulte l'astronome grec Sosigène qui lui conseille de ne pas tenir compte du cycle de la Lune, mais de suivre au mieux le cycle des saisons qu'il évalue à 365,25 jours.
Pour rattraper le retard accumulé, Jules César décide d'attribuer 455 jours à l'année en cours, appelée année de confusion. L'année comportera désormais 365 jours et pour compenser le quart de jour manquant, tous les quatre ans, l'année comportera 366 jours ; c'est l'année bissextile.
Mais en 730, le calendrier se retrouve à nouveau en retard d'une semaine par rapport au cycle du Soleil, mais rien n'est décidé jusqu'au 16° siècle. En 1582, le Pape Grégoire XIII demande à un groupe de savants de lui proposer des solutions. Ils constatent que le calendrier julien prend trois jours de retard en quatre siècles et suggèrent de supprimer certaines années bissextiles : les années séculaires (celles dont le numéro est divisible par 100) non divisibles par 400 ne seront plus bissextiles. De plus, il faut rattraper le retard accumulé : Grégoire décide que le Jeudi 4 Octobre 1582 sera suivi immédiatement par le Vendredi 15 Octobre.
Le 12 septembre 2007, un journaliste déclare à la radio que l'Ethiopie est passée ce jour 12/09/2007 au deuxième millénaire. Il explique cela par le fait que l'Ethiopie serait restée au calendrier julien. Commentez et justifiez votre réponse.
Nombre d'années écoulées : 730
+ 46 = 776.
Retard par année : 365,25 - 365,2422 = 7,8.10-3
Retard cumulé : 776 x 7,8.10-3 = 6,05 jours, soit
environ une semaine.
Retard accumulé par le calendrier julien en quatre
siècles :
400 x 7,8.10-3 = 3,12 jours. le rapport des savants est
correct et d'une bonne précision.
Retard cumulé de - 46 à + 1582 = (1582 + 46) 7,8.10-3 = 12,7 jours.
Le calendrier grégorien attribue à l'année
une durée de 365 + 0,25 (1 - 3/100) = 365,2425. En effet en quatre
siècles,
il y a 100 (400 / 4) années bissextiles, dont
3 sont retirées (années séculaires non divisibles
par 400, donc par exemple
100, 200 et 300). Autre calcul possible : durée de l'année grégorienne : 365 + 1 x 97 / 400.
L'erreur est un retard de 365,2425
- 365,2422 = 3.10-4 jour par an. Pour que ce retard cumulé
atteigne un jour, il faudra : 1 / 3.10-4 , soit environ 3333
ans, auxquels il faut ajouter 1582, donc environ 4915, soit entre 4000 et 5000. Nous aurons le temps
de réagir ! Remarquez que la durée de
l'année tropique est donnée avec 7 chiffres
significatifs, ce qui correspond à une très grande
précision. Mais que du fait de la dernière
soustraction, il ne reste plus qu'un seul chiffre significatif, ce qui
conduit à une grande incertitude sur le dernier
résultat.
Le calendrier cosmique ramène la durée de l'Univers
(quinze milliards d'années) à une année. Si on imagine
que l'Univers est né le premier Janvier à 0 heure, les premières
galaxies se sont formées le 2 Janvier. Le 10 Septembre à
midi, le Soleil est apparu, le système Terre-Lune est né
le 13 Septembre, la vie est apparue sur Terre le 15 Octobre, les dinosaures
le 24 Décembre, notre ancêtre Lucy le 31 Décembre à
21 heures. A 23 heures 59 minutes et 50 secondes, les Égyptiens
construisent les pyramides et à 23 heures 59 minutes 59,937 secondes,
l'Homme marche sur la Lune. Le premier Avril suivant, notre Soleil devient
une géante rouge et détruit la Terre.
1 seconde correspond à 475 années, une
heure à 1,7 million d'années, un jour à 41 millions
d'années.
Le Soleil a 4,6 milliards d'années.
La vie est apparue sur Terre il y a 3 milliards d'années.
La Terre s'est formée il y a 4,5 milliards d'années, mais
il a fallu du temps pour que sa température s'abaisse, afin que
la vie y devienne possible.
Les premières galaxies sont vieilles de 15 milliards
d'années. Il ne peut y avoir de vie sur les planètes éventuellement
en orbite autour d'elles (ou du moins sur les images que nous recevons
aujourd'hui de systèmes actuellement disparus) car les éléments
indispensables à la vie, carbone, oxygène ne sont pas encore
formés. Ces éléments formés par les étoiles
ne seront disponibles qu'après explosion de celles-ci, donc à
la deuxième génération d'étoiles comme le Soleil.
Le Soleil absorbera la Terre dans 3,7 milliards d'années.
Sommaire : Les premières horloges, le cadran
solaire, la clepsydre, le sablier, les horloges mécaniques, les
horloges électroniques, les horloges atomiques, pourquoi cette recherche
de précision ? travaux pratiques : Le pendule simple, mesure de
la fréquence et de la période du signal délivré
par un générateur basse fréquence.
De même que le développement de l'agriculture a conduit
les hommes à concevoir des calendriers, le développement
de la vie sociale a imposé la construction d'horloges.
Initialement, il était constitué d'un gnomon, bâton
planté verticalement dans le sol. Il fut perfectionné par
les Égyptiens, puis les Grecs.
Le cadran solaire est une horloge qui utilise le mouvement apparent du Soleil.
Inventée en Égypte, au 15 ° siècle avant
notre ère. Son nom signifie 'voleuse d'eau'. On mesure la quantité
d'eau s'écoulant d'un vase percé.
Le sablier et la clepsydre ne déterminent pas l'heure, mais
mesurent des durées : Ce sont des chronomètres.
Le sablier est encore en usage de nos jours, dans un but essentiellement décoratif. Il fut un temps où il constituait à bord des navires un instrument de mesure du temps, indispensable pour déterminer la longitude. La vie à bord était (est encore) réglée par les quarts, indiqués par un sablier. Les petits malins qui retournaient le sablier pour raccourcir leur quart faisaient perdre au capitaine la position de son navire. La punition était le passage du fautif d'un bord à l'autre, sous la quille du navire en marche, attaché à une corde. Les temps étaient durs. Avis à ceux qui rêvent d'un Paradis perdu qui n'a jamais existé.
L'horloge à poids est inventée en 996. En 1600 Galilée
découvre les lois du pendule simple (voir le travail pratique n°
1) alors que ses contemporains pensaient que les pendules oscillaient sous
l'effet du vent (donc irrégulièrement). En 1657 Huygens invente
l'horloge à balancier. En 1610, Galilée découvre les
satellites de Jupiter. Leur mouvement régulier, facile à
observer, incite certains savants à s'en servir pour mesurer le
temps. Mais on découvre une irrégularité dans ce mouvement
que Ròmer attribue en 1675 à la vitesse de propagation de
la lumière, mesurée ainsi pour la première fois.
Principe de l'horloge à quartz :
ou -> circuit d'affichage -> afficheur
// Note : Contrairement à ce que laisse penser un 'calcul
de précision' sur un ouvrage scolaire, la précision de l'oscillateur
à quartz est très grande. Ce n'est en aucun cas 32768 Hz
à + - 1 Hz.
Exercice : Pourquoi avoir choisi cette fréquence ?
Réponse : 32768 = 2 15. Il suffit donc de 15 étages électroniques successifs, divisant chacun la fréquence par 2, pour obtenir un signal de sortie à 1 Hz qui pilote les aiguilles ou l'afficheur. Note : Certaines montres ont des aiguilles des secondes qui avancent d'une seconde non pas en une seule fois, mais en plusieurs. Leur prix est plus élevé.
La première fut fabriquée en 1947. L'horloge atomique
au césium sert à définir la seconde. Une bonne horloge
atomique dérive de 1 seconde en 3 millions d'années.
Le refroidissement laser des atomes (Le français Cohen Tannoudji,
prix Nobel de Physique en 1997) permettra de multiplier par 1000 cette
précision.
Dans notre bonne vieille ville de Besançon, se trouvent (à
la date de réalisation de cette page) 4 horloges atomiques.
La possession d'une horloge aussi précise que possible permet
de connaître la position d'un navire. Les meilleures horloges mécaniques
au 17° siècle (horloge à ressort spiral, comme les anciennes
montres mécaniques) permettaient de connaître la position
d'un île dans l'Atlantique à quelques kilomètres près.
Pas étonnant donc que Lapérouse ait rayé de la carte
de l'Atlantique quelques îles, et déplacé plusieurs
autres. Aujourd'hui, les horloges atomiques embarquées à
bord de satellites permettent de se positionner (navires, avions, véhicules
terrestres...) à 100 voire 10 mètres près. Des relais
fixes permettent des mesures au millimètre près (étude
de la dérive des continents). Les américains disposent du
GPS, les Européens de EGNOS, les Russes de leur propre système.
Pages 270 et suivantes, exercices n° 24, 25, 26, 27.
doit dépendre la période d'un pendule ? Une fois ces
paramètres identifiés, vous vous emploierez à n'en
faire varier qu'un seul à la fois.
Comment mesurez-vous cette longueur ?
Mesurez plusieurs fois de suite la période de ce pendule simple
; notez vos résultats.
Comment pouvez-vous améliorer la précision de vos mesures
?
Réponses : Il semble logique de mesurer la longueur du pendule de son point de suspension jusqu'au centre de gravité de la masse qui y est attachée. Pour améliorer la précision des mesures, mesurer plusieurs périodes (10 par exemple) ; déclencher le chronomètre à l'instant où le pendule va le plus vite, c'est à dire lorsqu'il repasse par sa position d'équilibre.
Mesurez soigneusement la période.
// Note : Une erreur fréquente des élèves consiste à compter 9 périodes au lieu de 10.
Prenez 5, 10, 15 et 80 degrés d'amplitude. Mesurez la période.
Conclusion ?
Pour les faibles angles, la période du pendule ne dépend
pas de l'angle. //On parle d'isochronisme des petites oscillations.
Lorsque l'angle devient important, la période augmente un peu.
Quelle amplitude angulaire choisissez-vous ? Conclusion ?
Nous choisissons une faible amplitude (afin que sa valeur n'intervienne pas dans les résultats). La période ne dépend pas de la masse.
Prenez une longueur de 30 cm. Mesurez la nouvelle période.
Est-elle 2 fois plus courte ? Trouvez le rapport des deux périodes.
Pour qu'un pendule ait une période double de celle du pendule de
60 cm, quelle devrait être sa longueur ?
Pourquoi les horloges à balancier, basées sur le principe
du pendule, font-elles de bonnes horloges terrestres, mais de mauvaises
horloges marines ?
La précision d'une mesure à l'oscilloscope est inférieure à 1 %.
Une période se mesure lors du passage à zéro de la tension.