Le B.O. N° 7, 31 AOÛT 2000 PH Y
S I Q U E - C H I M I E CLASSE DE PREMIÈRE SÉRIE SCIENTIFIQUE
HORS-SÉRIE PROGRAMME DE PHYSIQUE
(durée indicative: 3 heures, 1 TP)
Objectifs
Dans cette partie introductive, il s’agit de poursuivre la mise en
place, entamée en classe de seconde dans la partie “échelles
de distances et de tailles”, des différents niveaux de structuration
de la matière, du microscopique au macroscopique, en précisant
les interactions dominantes à chaque échelle. Plus précisément,
on illustre les deux idées suivantes :
- la diversité de la matière : noyaux, atomes et molécules,
phases condensées ou gazeuses, organismes vivants, systèmes
astronomiques, résulte de l’arrangement de trois “briques “de base,
protons, neutrons et électrons, considérées au lycée
comme particules élémentaires.
- la cohésion de ces assemblages est assurée par trois
interactions fondamentales :
l’interaction forte, de courte portée, qui contrebalance la
répulsion entre protons et assure ainsi la cohésion des noyaux
jusqu'à l’uranium,
l’interaction électromagnétique qui, par son aspect électrique,
est responsable de la cohésion des atomes, des molécules
et des phases condensées,
l’interaction gravitationnelle qui, bien que d’intensité beaucoup
plus faible que les autres, gouverne la structure de la matière
à grande échelle, car elle est de longue portée et
toujours attractive.
| EXEMPLES D’ACTIVITÉS | C O N T E N U S | CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES |
| Illustrer par des études documentaires*, le fait que, du noyau
atomique jusqu’aux systèmes astronomiques, la matière peut
être considérée comme constituée de neutrons,
protons et électrons.
Observer et interpréter, à l’échelle atomique, les phénomènes tels que: -l’électrisation par frottement, -l’attraction et la répulsion d’objets, -le caractère conducteur ou isolant de certains matériaux. Observation sur une carte (N,Z) du domaine d’existence des noyaux atomiques. Comparaison des interactions électrique et gravitationnelle pour
le système électron proton.
|
1 - Particules élémentaires
Les constituants de la matière: neutrons, protons, électrons. Charge élémentaire. 2 - Interactions fondamentales - La masse et l’interaction gravitationnelle ; loi de Newton. - Les charges et l’interaction électrique; loi de Coulomb; direction, sens, valeur: F = kqq’/d2 avec k ~= 9.109 S I Phénomènes d’électrisation. Isolants. Conducteurs ; porteurs de charge: électrons et ions. - Les nucléons et l’interaction forte. Deux interactions à l’oeuvre dans le noyau : la répulsion coulombienne entre protons compensée, jusqu’à l’uranium, par une interaction attractive intense mais de courte portée. 3 - Interactions et cohésion de la matière échelle astronomique, - échelle atomique et humaine échelle du noyau. |
Savoir que toute charge électrique est multiple d’une
charge élémentaire.
Connaître l’ordre de grandeur du rapport des masses du nucléon et de l’électron. Connaître l’ordre de grandeur du rayon d’un atome et d’un noyau. Réaliser et interpréter des expériences simples mettant en jeu des phénomènes d’électrisation. Connaître et savoir appliquer la loi de Coulomb. Savoir que dans un métal une fraction des électrons est libre de se déplacer dans tout l’échantillon, alors que dans un isolant les déplacements des charges sont inférieurs à la taille atomique. Savoir qu’au niveau du noyau s’exercent deux types d’interactions dont les effets sont opposés. Savoir que la cohésion de la matière est assurée à diverses échelles par : - l’interaction gravitationnelle à l’échelle astronomique, - l’interaction électromagnétique à l’échelle des atomes, des molécules et de la matière à notre échelle, - l’interaction forte à l’échelle du noyau. |
* Activités pouvant donner lieu à l’utilisation des technologies de l’information et de la communication
L’interaction gravitationnelle a déjà été
rencontrée en classe de seconde. De l’interaction électromagnétique,
seul l’aspect électrique est ici présenté. La force
d’interaction entre deux charges est précisée : direction,
sens, valeur F = k qq’/d2
avec k @ 9,3.109 S I ; elle est
représentée sur les schémas par une flèche
mais aucune expression vectorielle de cette force n’est à donner.
Une autre manifestation de l’interaction électromagnétique,
l’action d’un champ magnétique sur un courant (particules chargées
en mouvement), est présentée dans la partie III.B.
Une approche expérimentale des phénomènes d’électrisation
permettra de justifier l’existence des deux types de charges et de préciser
la nature attractive ou répulsive de leur interaction. Lorsque l’enseignant
parle d’électrisation, le mot est pris dans un double sens : arrachage
ou apport d’électrons (électrisation par contact), et déplacement
interne de charges (phénomènes de polarisation) ; dans ce
dernier cas, on se contente d’interpréter qualitativement les phénomènes
par une distorsion locale de la distribution de charges, l’emploi du mot
“polarisation “n’est pas exigé.
L’enseignant indiquera, en prenant divers exemples (tension d’un fil,
résistance mécanique de la matière, ressort...), que
l’interaction électromagnétique est responsable de la cohésion
de la matière à notre échelle (y compris la matière
vivante) mais veillera cependant à ne pas induire l’idée
qu’elle suffit à elle seule à l’expliquer (la mécanique
quantique joue un rôle fondamental).
L’interaction forte, qui n’est que citée à ce niveau,
est présentée dans le cadre de la cohésion du noyau
: si le noyau résiste à la forte répulsion entre protons,
c’est qu’il existe une interaction attractive entre nucléons. On
fait remarquer que lorsque le nombre de charges augmente, la répulsion
électromagnétique finit par l’emporter : le tableau périodique
des éléments naturels s’arrête ainsi à l’uranium.
L’interaction faible ne sera pas introduite.
La prédominance habituelle de l’interaction gravitationnelle
sur Terre est expliquée par la quasi-neutralité électrique
des objets macroscopiques et la grande masse de la Terre ; on remarque
de plus que l’interaction gravitationnelle est négligeable entre
deux objets de taille ordinaire.
Sommaire : Travail personnel, charges électriques,
mise en évidence par des expériences d'électrisation
par frottement ou par contact, charges positives et charges négatives,
au niveau microscopique, atome, charge électrique élémentaire,
interaction électrique, loi de Coulomb, conducteurs et isolants.
Recherchez la signification des termes suivants, et proposez des
applications des phénomènes correspondants : Electrophorèse,
foudre,
paratonnerre,
électrostatique.
// Les expériences d'électrostatique
posent souvent problème en présence d'élèves,
car l'humidité ambiante décharge rapidement les corps électrisés.
Prévoir le matériel suivant :
Chiffon de laine (je trouve la peau de chat barbare et allergisante),
bâtons en verre, règles en matière plastique, pendule
électrostatique, électroscope, tiges métalliques,
corps isolants (bois, matière plastique), petits tubes au néon
(du type de ceux qui se trouvent dans les tournevis testeurs ; c'est la
borne reliée au moins qui devient lumineuse), machine de Wimshurst,
supports de physique, supports isolant (blocs de polystyrène expansé),
balance au 1 / 100 de gramme.
Un voltmètre numérique, en calibre continu, muni
de deux fils, le fil relié à la borne com simplement posé
sur la table, peut servir de détecteur de charges.
L'ensemble des expériences sur les charges électriques
ne mettent en évidence que deux types de charges, positives
ou négatives.
Des charges de même signe se repoussent ; des charges de signe contraire s'attirent.
Un corps portant la même quantité de charges positives et négatives est électriquement neutre.
L'atome est électriquement neutre ; il est constitué
d'un noyau chargé positivement autour duquel gravitent des électrons
chargés négativement.
Par frottement, des électrons périphériques sont transférés de la laine vers le PVC ou du verre vers la laine. L'électrisation par frottement consiste à créer sur un corps un excès d'électrons et sur un autre un défaut d'électrons.
Une charge électrique se mesure en coulombs, symbole C.
L'électron porte une charge électrique notée - e = - 1,6 . 10-19 C. La valeur absolue de cette charge est appelée charge élémentaire.
Le proton porte une charge élémentaire. Le neutron est électriquement neutre.
Dans toutes les expériences d'électrisation, nous mettons en jeu des nombres entiers de charges élémentaires.
Rappelons quelques propriétés des constituants de la matière :
| Charge électrique en coulombs | Masse en kilogrammes | |
| Électron | - 1,6 . 10-19 | 9,1.10-31 ou 0,9.10-30 |
| Proton | + 1,6 . 10-19 | 1,6.10-27 ou 1,673.10-27 |
| Neutron | 0 | 1,6.10-27 ou 1,675.10-27 |
Rappelons aussi :
Rayon d'un atome, environ 2.10-10 m, ou 0,2 nm (nanomètre).
rayon d'un noyau, environ 5 fm (femtomètres), ou 5.10-15
m.
La charge élémentaire aujourd'hui admise (Union Internationale
de Physique Pure et Appliquée, ou norme Afnor 1989) est :
e = 1,60217733 . 10-19 C avec une incertitude de 0,30 . 10-6,
soit + ou - 48 sur les deux derniers chiffres (33).
Une valeur admise auparavant était 1,6021892
. 10-19 C. Elle était fausse par suite d'une grave
erreur des physiciens chargés de la mesure et de ceux chargés
de vérifier leur résultat. C'est cette valeur fausse qui
est parfois gravée dans la mémoire de certaines calculatrices.
La charge de l'électron et celle du proton sont exactement
opposées (vérification expérimentale avec 40 chiffres
significatifs).
Deux charges ponctuelles qA et qB, placées
dans le vide ou dans l'air, en A et B, séparées par une distance
AB = r, exercent l'une sur l'autre deux forces directement opposées,
de valeur :
 |
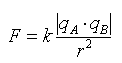Les deux forces ont même support (ou droite d'action), la droite (AB) ; les forces sont répulsives si les deux charges sont de même signe, attractives dans le cas contraire.
Les conducteurs comportent des charges électriques mobiles,
électrons dans les métaux, ions dans les électrolytes.
Dans un isolant, aucune charge électrique ne peut se déplacer.
Analyse préliminaire :
Vous avez déjà remarqué que lorsque vous vous
brossez les cheveux ceux-ci se dressent sur votre tête et sont
attirés par la brosse quand vous l’éloignez.
Proposer une explication de ce phénomène.
Étude expérimentale du phénomène d’électrisation :
Vous disposez du matériel suivant : tiges de divers matériaux ( verre, plexiglas, ébonite, PVC, bois, métal) et de petits pendules électrostatiques (boule de polystyrène enrobé d’aluminium, suspendu à un fil), tissu de laine, peau de chat…
1- Proposer et interpréter une expérience montrant que
l’on peut électriser certains matériaux par frottement. Tous
les matériaux ont-ils le même comportement ? Proposer un classement.
2- Proposer et interpréter une expérience montrant que
l’on peut électriser un corps par simple contact.
3- Proposer une expérience montrant le caractère conducteur
d’un métal et le caractère isolant du bois sec.
4- Proposer et interpréter une expérience montrant que
deux charges de même signe se repoussent et que deux charges de signes
contraires s’attirent.
5- En admettant que le verre est un matériau qui s’électrise
positivement, rechercher expérimentalement un matériau
qui s’électrise comme le verre et un matériau qui s’électrise
de façon différente.
Décharge d’un corps électrisé :
Pour électriser un corps on peut utiliser une machine de Wimshurst
qui génère de très fortes tensions.
Expliquer son fonctionnement (voir livre page 21 doc 1)
Pourquoi observe-t-on un arc électrique ?
Bilan
Comment classer les électrisations que l’on vient d’étudier
? Que se passe-t-il au niveau des charges électriques ?
Un isolant est-il isolant dans toutes les conditions ?
// Le lecteur pourra consulter le chapitre "Olympiades
de la Physique", où il trouvera la description d'un montage facilement
réalisable permettant d'obtenir, rapidement et en présence
de public, un ordre de grandeur de la constante de gravitation
universelle.
Cette interaction est à l'origine de l'existence et de la forme des étoiles, des planètes et de leur mouvement relatif ; elle est responsable de la pesanteur.
Les forces gravitationnelles ont une portée infinie et sont toujours attractives. Leur intensité est faible, mais leur effet est cumulatif.
// Bien que l'interaction gravitationnelle soit la première qui ait fait l'objet d'une étude quantitative (Newton : 1687, Cavendish : 1798), de nouvelles recherches sont en cours, car des anomalies ont été constatées pour les distances moyennes. Non seulement la constante de gravitation universelle, G, n’est pas connue avec une grande précision, contrairement aux autres constantes physiques, mais en 1998, les physiciens ont dû revoir à la hausse les incertitudes sur sa mesure, qui sont passées de 0,013 % (1987) à 0,15 %.
La norme Afnor de 1989, reproduite dans certains livres de cours de première S, donne G = 6,67259 . 10-11 m3 . s-2 . kg-1, avec une incertitude de + ou - 0,013 % soit une variation possible de + ou - 85 sur les deux derniers chiffres (59), alors que la valeur tabulée, admise depuis 1998 est G = 6,67 . 10-11 m3 . s-2 . kg-1 à + ou - 0,15 % soit + ou - 1 sur le dernier chiffre (7).
La propagation de la gravitation fait actuellement l'objet de recherches très poussées (expérience Européenne VIRGO, expériences américaines...).
Deux corps ponctuels A et B, de masses mA et mB, séparés par une distance AB = r, exercent l'un sur l'autre deux forces attractives, directement opposées, de valeur :
 |
Elle est responsable de la cohésion des objets, des liaisons
chimiques, des forces de contact, des forces de frottement, de la dureté
et de la forme des matériaux.
Elle a une portée infinie. Elle est beaucoup plus forte que
l'interaction gravitationnelle. Mais il n'y a pas d'effet cumulatif.
L'un de ses aspects a déjà été évoqué : La loi de Coulomb.
Les interactions entre charges en mouvement sont responsables du magnétisme, autre forme de l'interaction électromagnétique.
La cohésion d'un noyau atomique, formé de neutrons
et de protons, ne peut pas être assurée par l'interaction
électromagnétique (répulsive entre protons), ni par
l'interaction gravitationnelle, bien trop faible. Il faut donc admettre
l'existence d'une autre interaction fondamentale, appelée forte.
Sa portée ne dépasse pas le noyau atomique ; elle agit entre les quarks qui constituent les nucléons, neutrons et protons. Elle est 100 à 1000 fois plus intense que l'interaction électromagnétique. Elle est responsable des réactions nucléaires dans les étoiles, les centrales atomiques et les... bombes.
La cohésion de la matière est assurée par :
| Interaction gravitationnelle | Interaction électromagnétique | Interaction faible (effet quantique) | Interaction forte (nucléaire) |
| Porte à l'infini (importante à l'échelle astronomique, par effet cumulatif) | Porte à l'infini, très intense, mais pas d'effet cumulatif car les charges tendent à se compenser | Échelle atomique | Dans le noyau atomique |
| Attractive | Attractive ou répulsive selon le signe de la charge. | Répulsive | Attractive |
Loi de Newton, cours de 2nde
 |
Loi de Coulomb, cours de 1°S
 |
Page 39, exercices 12 (QCM) , 16 (masse attirée par la Terre
et le Soleil, discussion sur l'effet de marée), 17 (mesure de G
par Cavendish), 35 (conjonction inférieure Terre Lune Soleil), 39
(très difficile, forces dans un cristal ionique).
Supplément : Ex. 34,38 p.40 (exercices sur force de gravitation)
Les interactions, Richard FEYNMAN
« Considérons
une force analogue à la gravitation qui varie comme l’inverse du
carré de la distance, mais qui soit environ un milliard de milliards
de milliards de fois plus intense. Et avec une autre différence.
Il y a deux espèces de matière, que nous pouvons appeler
positive et négative. Celles de même espèce se repoussent
et celles d’espèces différentes s’attirent, contrairement
au cas de la gravité où il y a seulement attraction. Que
va-t-il se passer ?
Un amas d’éléments
positifs se repousserait avec une force énorme et éclaterait
dans toutes les directions. Un amas d’éléments négatifs
en ferait autant. Mais un mélange égal d’éléments
positifs et négatifs ferait quelque chose de tout à fait
différent. Les éléments opposés seraient maintenus
ensemble par des attractions énormes. Le résultat global
serait que les forces terrifiantes s’équilibreraient entre elles
presque parfaitement en formant des mélanges fins et serrés
d’éléments positifs et négatifs, et entre deux amas
d’un tel mélange, il n’y aurait pratiquement pas du tout d’attraction
ou de répulsion.
Une telle force existe :
c’est la force électrique. Et en toute matière est un mélange
de protons positifs et d’électrons négatifs qui s’attirent
et se repoussent avec cette grande force. L’équilibre est si parfait
cependant, que lorsque vous vous tenez près de quelqu’un d’autre,
vous ne sentez aucune force. S’il y avait un très léger déséquilibre
vous le sauriez. Si vous vous teniez à un bras de distance de quelqu’un
et que chacun de vous ait un pour cent d’électrons de plus que de
protons, la force de répulsion serait incroyable. De quelle grandeur
? Suffisante pour soulever l’Empire State Building ? Non ! Pour soulever
le Mont Everest ? Non ! La répulsion serait suffisante pour soulever
une masse égale à celle de la Terre entière !
Avec des forces aussi énormes
et aussi parfaitement équilibrées dans ce mélange
intime, il n’est pas difficile de comprendre que la matière, essayant
de garder ses charges positives et négatives dans le meilleur équilibre,
puisse avoir une grande rigidité et une grande résistance.
»
L’Empire State Building,
par exemple, ne s’écarte que de 2,50 m de son équilibre parce
que les forces électriques maintiennent chaque électron et
chaque proton plus ou moins à sa propre place…
Vous savez évidemment
que les atomes sont constitués de protons positifs dans le noyau
et d’électrons à l’extérieur. Vous pouvez vous demander
: si cette force électrique est si terrifiante, pourquoi les
protons et les électrons ne collent-ils pas les uns sur les autres
? S’ils veulent former un mélange intime, pourquoi celui-ci n’est-il
pas encore plus intime ? La réponse fait intervenir des effets quantiques
…
Une autre question se pose
: qu’est ce qui maintient le noyau compact ? Dans le noyau il y a plusieurs
protons qui sont tous positifs. Pourquoi ne se repoussent-ils pas ? Il
s’avère que dans le noyau il y a, en plus des forces électriques,
des forces non électriques, appelées forces nucléaires,
qui sont plus grandes que les forces électriques et qui sont capables
de maintenir les protons ensemble malgré la répulsion électrique.
Les forces nucléaires, cependant, sont à court rayon d’action
– leur intensité décroît beaucoup plus rapidement que
1 /
R2 . Et ceci a une conséquence importante. Si un
noyau contient trop de protons, il devient gros, et il ne restera pas compact.
Un exemple est fourni par l’uranium, avec 92 protons. Les forces nucléaires
agissent principalement entre chaque proton (ou neutron) et son plus proche
voisin, tandis que les forces électriques agissent sur de plus grandes
distances, donnant une répulsion entre chaque proton et tous les
autres protons du noyau. Plus il y a de protons dans le noyau, plus forte
est la répulsion électrique, jusqu’à ce que, comme
dans le cas de l’uranium, l’équilibre devienne si fragile que le
noyau est presque prêt à éclater sous l’action de la
force électrique de répulsion… »
Richard FEYNMAN
Questions :
Réaliser un tableau
avec les 4 types d’interactions.
Préciser leur nom,
leur portée (petite, grande … distance), leur effet et la formule
permettant de calculer la force correspondante dans les cas déjà
connus.
Essayez de vérifier
l'affirmation de Richard Feynman : "La répulsion serait suffisante
pour soulever une masse égale à celle de la Terre entière
!".
(durée indicative 18 heures, 6 TP)
A - FORCES ET MOUVEMENTS
Objectifs
L’idée est de reprendre et d’approfondir les notions vues en
seconde en montrant comment une action s’exerçant sur un solide
est capable de modifier son mouvement.
L’un des objectifs est de préciser la conception newtonienne
du mouvement selon laquelle la force est liée au changement de la
vitesse et non à la vitesse. Ce travail a déjà été
entrepris en classe de seconde avec une première approche du principe
de l’inertie et de la force de gravitation.
Il s’agit maintenant de donner davantage de consistance au point de
vue newtonien en étendant le champ de l’étude à celle
de solides soumis à plusieurs actions simultanées, le cas
du solide en translation étant privilégié. Le mouvement
du centre d’inertie d’un solide est le principal objet de l’étude,
mais pour autant il ne s’agit pas de présenter la mécanique
du “point matériel” mais d’aborder celle de systèmes réels
par celle du système matériel le plus simple, le solide.
| EXEMPLES D’ACTIVITÉS | C O N T E N U S | CONNAISSANCES ET SAVOIR-FAIRE EXIGIBLES |
| Observation du mouvement du centre d’inertie.
Observation des mouvements des autres points (vidéos, chronophotographies...) *. Réalisation et exploitation d'enregistrements : table à coussin d’air, table à digitaliser, vidéos, capteurs chrono-cinés*... Détermination de vecteurs vitesses à partir d’enregistrements. Étude du mouvement du centre d’inertie d’un solide dans diverses situations (projectiles, satellites). Recherche de forces sur des exemples variés (expériences, vidéos, logiciels...)*. Utilisation du principe d’inertie pour analyser les forces qui agissent sur un solide, en mouvement ou non. Mettre en relation la variation du vecteur vitesse VG d’un mobile avec la somme des forces appliquées dans des situations simples et variées. Expliquer pourquoi il y a des ceintures de sécurité dans les voitures. Analyser comment le principe d’inertie s’applique à un véhicule qui monte une côte rectiligne à vitesse constante. Expliquer le rôle des roues motrices et du sol dans le mouvement d’une voiture.
|
1 - Mouvement d’un solide indéformable
1 . 1 Vecteur vitesse d’un point du solide 1 . 2 Centre d’inertie d’un solide 1 . 3 Mouvement de translation d’un solide 1 . 4 Mouvement de rotation d’un solide autour d’un axe fixe ; vitesse angulaire 2 - Forces macroscopiques s’exerçant sur un solide Actions exercées sur un solide ; exemples d’effets produits (maintien en équilibre, mise en mouvement de translation, mise en mouvement de rotation, déformations). 3 - Une approche des lois de Newton appliquées au centre d’inertie 1ère loi : Principe d’inertie Ce principe n’est vrai que dans certains référentiels. Ces référentiels sont dit galiléens. 2ème loi: Aspect semi-quantitatif: comparaison de la somme des forces et de la variation du vecteur vitesse du centre d’inertie dans un référentiel galiléen. -3ème loi : Principe des actions réciproques |
Sur un enregistrement réalisé ou donné,
déterminer et représenter le vecteur vitesse V d’un point mobile Savoir que le vecteur vitesse V est le même pour tous les points d’un solide en translation. Savoir que chaque point d’un solide en rotation autour d’un axe fixe a une trajectoire circulaire. Pour un solide en rotation autour d’un axe fixe, relier la vitesse d’un point à la vitesse angulaire. Identifier et représenter les actions qui s’exercent sur un solide. Prévoir dans des cas simples la possibilité de mise en rotation d’un solide autour d’un axe fixe . Connaître et appliquer les lois de Newton : - Dans un référentiel galiléen, si le vecteur vitesse VG du centre d’inertie ne varie pas, la somme F=Sf des forces qui s’exercent sur le solide est nulle et réciproquement. - Dans un référentiel galiléen, si le vecteur vitesse VG du centre d’inertie varie, la somme F= Sf des forces qui s’exercent sur le solide n’est pas nulle. Sa direction et son sens sont ceux de la variation de VG entre deux instants proches . A et B étant deux corps, soient FB / A la force exercée par B sur A et FA / B la force exercée par A sur B. Quel que soit l’état de mouvement de A par rapport à B on a toujours l’égalité vectorielle : FA / B = - FB / A Analyser un exemple où une force de frottement sert à la propulsion. |
* Activités pouvant donner lieu à l’utilisation des technologies de l’information et de la communication
Vitesse d’un point d’un solide.
La valeur de la vitesse moyenne est introduite comme le quotient de
la distance parcourue par la durée. La mesure approchée de
la valeur de la vitesse d’un point est obtenue par le calcul de la valeur
de la vitesse moyenne entre deux instants voisins.
Mouvement d’un solide
Connaître le mouvement d’un solide, c’est connaître le
mouvement de chacun de ses points.
L’étude, dans le référentiel terrestre, du mouvement
d’un solide soumis à la seule action de la Terre montre qu’il existe
un point G dont le mouvement est plus simple que les autres : le centre
d’inertie. Cette étude est conduite en référence à
un ou deux exemples concrets et simples de situations de dynamique. On
pourra, à cette fin, utiliser des enregistrements vidéo ou
chronophotographiques de mouvements judicieusement choisis.
Forces macroscopiques s’exerçant sur
un solide
La description microscopique des actions subies par un corps nécessite
en général la connaissance de tout un ensemble de forces
réparties en volume ou à la surface de contact avec les autres
corps ; pour l’étude du mouvement du centre d’inertie des corps,
la connaissance de la résultante de chacune de ces diverses actions
est suffisante, d’où la modélisation, à ce niveau,
de chacune de ces actions en terme d’une force unique, par exemple : “résultante
des forces de pesanteur” ou “résultante des forces de contact entre
solides”. Pour pouvoir mettre un solide en rotation autour d’un axe fixe,
la droite support d’une force ne doit pas passer par l’axe ni être
parallèle à cet axe. Les déformations élastiques
sont à citer car elles conduisent en particulier, après étalonnage,
à des appareils de mesure de forces (dynamomètres) .
Il est signalé aux élèves que les forces macroscopiques
qui s’exercent sur un solide (exception faite de celles de pesanteur) ont
pour origine l’interaction électromagnétique ; on fait ainsi
le lien entre le domaine de la mécanique et celui des interactions
fondamentales étudié dans la partie précédente.
Une approche des lois de Newton
On se limite à un niveau de formulation semi-quantitatif des
lois de Newton qu’on énoncera comme principes fondamentaux dans
un référentiel galiléen. Valables pour tout corps
même déformable, on se contentera ici de les appliquer à
des solides.
La première loi permet de retrouver le principe d’inertie. Pour
son application, le référentiel terrestre et le référentiel
géocentrique seront considérés comme galiléens.
L’approche quantitative de la deuxième loi s’appuie sur le constat
d’une variation DVG de la vitesse du centre d’inertie calculée entre
deux instants proches. La relation F = m a sera vue en classe terminale
; seuls la direction et le sens des vecteurs F et DVG seront comparés
en classe de première (cas où la somme des forces est nulle,
cas d’un mouvement rectiligne varié, cas d’un mouvement curviligne
varié, cas d’un mouvement circulaire uniforme).
Pour la troisième loi, on dit que deux corps A et B sont en
interaction si l’état de mouvement ou de repos de l’un (A) dépend
de l’existence de l’autre (B). Une interaction entre deux corps A et B
suppose toujours deux actions réciproques : celle de A sur B et
celle de B sur A. Une expression plus complète de la troisième
loi doit prendre en compte les moments des forces; cela ne sera pas abordé
ici. De plus on évitera l’emploi de l’expression “loi de l’action
et de la réaction” qui peut induire l’idée fausse d’une “réaction”
causée par une “action” et lui faisant suite temporellement.
Il est intéressant de faire remarquer aux élèves
que la résultante des forces de frottements s’exerçant sur
un mobile peut être dirigée dans le sens opposé à
la vitesse du mobile (freinage) mais aussi dans le même sens (propulsion).
On se limite dans ce programme au mouvement du centre d’inertie ; dans
l’application des deux premières lois à ce point, pour effectuer
la somme des forces, les vecteurs qui les décrivent seront représentés
graphiquement à partir d’une origine commune; ce point peut être
le centre d’inertie ou de préférence un point en dehors de
la figure représentant le dispositif étudié.
Sommaire : Travail personnel, vitesse d'un point,
vitesse moyenne : définition, rappel ; vitesse instantanée,
vecteur vitesse, centre d'inertie d'un solide, quelques mouvements particuliers
pour un solide : translation, rotation autour d'un axe fixe ; travail pratique.
Lors d'un déplacement, vous vérifiez la vitesse de
votre véhicule. Plusieurs vitesses peuvent être définies
; comment les mesurez ou les calculez-vous ?
Vous effectuez plusieurs tours sur la piste d'un stade, à vitesse constante. Pourtant, votre vitesse n'est pas la même en deux points opposés de la piste. Quelles sont les différences ? Quel modèle mathématique permettrait de décrire votre vitesse ?
Lancez (prudemment) un objet rigide (appelé solide) dans un mouvement quelconque (c'est à dire en le jetant et en lui donnant un mouvement de rotation). Le mouvement d'un point quelconque est-il simple à décrire ? Y a-t-il un point de l'objet dont le mouvement semble moins compliqué ?
Vous vous déplacez sur un vélo. Considérez le système cycliste + vélo. Ses points ont-ils tous le même mouvement ? Ce cas est-il plus simple ou plus compliqué que le précédent ?
Vous parcourez une distance D de 150 km en une durée T de 2 heures.
Votre vitesse moyenne est V = D / T, soit 75 km.h-1.
| La vitesse moyenne d'un mobile (exprimée en m.s-1) est numériquement égale au quotient de la distance parcourue (mesurée en m) par la durée du déplacement (en s). |
Il est évident que votre véhicule n'a pas roulé
à une vitesse constante de 75 km.h-1. La vitesse à
chaque instant est donnée par le compteur de vitesse, ou un radar
de la gendarmerie.
Comment la calculer ? En procédant au calcul précédent
de vitesse moyenne, mais sur des durées aussi courtes que possible,
donc pour des distances parcourues très petites.
| La vitesse instantanée v (t) d'un point, à la date t, est proche de la vitesse moyenne de ce point, calculée entre deux dates très voisines et encadrant la date t. |
Rappelez-vous le tour de piste, à "vitesse constante". En
fait, la valeur de votre vitesse était constante, mais pas sa direction
ni son sens.
Le vecteur vitesse instantanée d'un
point, à la date t, a :
|
Le vecteur vitesse d'un
point, à la date t, est représenté par un segment
fléché dont :
// Remarques : La norme est parfois appelée longueur
ou module ; le segment fléché, bipoint ou représentation
d'un vecteur.
| Lors du mouvement d'un solide, l'un des points décrit une trajectoire plus simple que celle des autres. Il est appelé centre d'inertie G du solide. |
// Remarque : Cette définition ne permet
pas de trouver par un calcul la position du centre d'inertie.
// Remarque : Voir le sujet de travail pratique
proposé, basé sur l'étude d'un fichier AVI.
// Voici un série de fichiers
AVI compressés, permettant l'étude de la chute libre
et la recherche du centre de gravité d'un triangle.
Le centre d'inertie est extrêmement proche du centre de gravité défini en classe de troisième.
Si un solide est homogène et admet un élément
de symétrie, son centre d'inertie appartient à cet élément
de symétrie. Le centre d'inertie d'une boule est son centre...
Si un solide est hétérogène, son centre d'inertie est plus proche des parties les plus lourdes.
Réponse : Le plus sur est le coupé, suivi dans l'ordre de la berline, l'utilitaire et la berline avec galerie et enfin le tout terrain. Pour les derniers, il y a risque de tonneau.
// Note : Avez-vous déjà remarqué sur la route le style des conducteurs de véhicules 4 x 4 ? N'avez-vous pas l'impression qu'ils confondent parfois leur véhicule utilitaire avec un véhicule de compétition ?
| Un solide est animé d'un mouvement de translation lorsque tout segment joignant deux points du solide se déplace parallèlement à lui-même. |
A un instant t quelconque, tous les points d'un solide en translation
ont le même vecteur vitesse instantanée.
Ce mouvement est uniforme si la valeur v de la vitesse reste
constante (ne varie pas au cours du temps).
Il est rectiligne lorsque tous les points parcourent des droites.
Les nacelles d'une grande roue ont des mouvements de translation circulaire, uniforme (sauf au départ et à l'arrêt).
Un disque vinyle sur sa platine, un disque compact dans le lecteur,
le mandrin d'une perceuse, une roue de voiture (dans le référentiel
lié à la voiture) sont animés d'un mouvement de rotation
autour d'un axe fixe.
Chaque point d'un solide animé d'un mouvement de rotation
autour d'un axe fixe se déplace dans un plan perpendiculaire
à l'axe, selon un arc de cercle. Les points n'ont pas tous
même valeur de la vitesse v ; ceux qui sont plus éloignés
de l'axe ont une vitesse v plus grande.
Par contre, pendant la même durée T, les rayons joignant
les points à l'axe tournent tous d'un même angle a.
Tous les points d'un solide en rotation autour d'un axe fixe ont
la même vitesse angulaire w définie
par w = a / T.
La vitesse angulaire w s'exprime en radian par seconde (rad.s-1), l'angle a en radian (rad) et la durée T en secondes.
La discussion sur vitesse angulaire moyenne et vitesse angulaire instantanée est identique à celle que nous avons eue à propos de la vitesse v (appelée aussi parfois, vitesse linéaire).
Si un solide est animé d'un mouvement de rotation autour
d'un axe fixe, de vitesse angulaire w, un point
de ce solide, situé à la distance R de l'axe, a une vitesse
(appelée parfois circonférentielle ou linéaire)
| v = w . R |
On appelle mouvement circulaire uniforme, un mouvement de rotation
autour d'un axe fixe tel que la vitesse angulaire w
soit constante.
Dans ce cas,
|
|
|
|
Exercice 1 : Le moteur d'une tondeuse à gazon tourne
à mi régime à 3000 tours par minute. La lame, fixée
sur l'arbre moteur a un diamètre de 50 cm.
Calculez la vitesse de rotation de la lame en tours par seconde et
sa pulsation en radians par seconde. Calculez la vitesse linéaire
d'un point situé à l'extrémité de la lame.
Malgré les conseils de sécurité délivrés
avec la tondeuse, un utilisateur pressé (et se croyant très
malin, alors que la suite va prouver le contraire), essaie d'enlever un
paquet d'herbe situé près de la lame, pas à la main
bien sur (il se croît très malin, alors que la suite va prouver
le contraire), mais à l'aide d'un bâton. Le bâton est
happé par la lame. Il faut 1 / 10 de seconde à l'utilisateur
(qui se croît très malin, alors que la suite va prouver le
contraire) pour lâcher le bâton. Quelle distance parcourt sa
main pendant cette durée ?
Expliquez, à partir de votre résultat :
Page 60, exercices 2 (astuce d'utilisation de la calculatrice pour les dates en h, min et s), 3 (vitesse instantanée pour un mouvement enregistré par pointage à intervalles de temps réguliers), 5 (compréhension du cours), 8 (vitesse angulaire), 11 (distance terre Soleil), 13 ajouter déterminer la distance parcourue à la date t2 (variations de vitesse), 27 (addition vectorielle des vecteurs vitesse).
Technique : Copiez ces 2 fichiers sur votre disque dur, afin
de ne pas bloquer l'accès réseau. Ouvrez-les l'un après
l'autre dans le logiciel LireAvi,
logiciel libre disponible sur ce site, ou WinLabo2 (Fichier
| AVI), ou aviMeca 2.3, ou Synchronie. Réglez l'échelle
verticale (la règle sur les images mesure 1,01 m). Pointez la position
du point qui vous intéresse par un clic gauche dans LireAvi qui
passe automatiquement à l'image suivante. Tant que
vous n'avez pas fermé le logiciel, les coordonnées des clics
sont mémorisées et l'échelle peut être corrigée.
Dans WinLabo 2, pointez par un clic droit et passez à
l'image suivante par un clic gauche sur la flèche de défilement.
Dans aviMeca 2.3, cliquez simplement sur le point qui vous intéresse
(clic gauche), le logiciel passant seul à l'image suivante.
Lorsque le film est terminé, transférez les mesures dans
Excel par Copier | Coller.
Tracez dans Excel les courbes y(t) et x(t).
Exploitation :
L'une des courbes devrait se rapprocher d'un segment de droite. Les
écarts que vous constatez sont-ils importants ? A quoi sont-ils
dus ? Comprenez-vous bien le rapport qu'il y a entre la courbe horizontale
x(t) = Cte et un phénomène de chute verticale
?
L'autre courbe semble un arc de parabole. Ajustez la parabole dans
Excel par un polynôme du second degré, en demandant l'équation
trouvée et le coefficient de régression. L'accélération
de la pesanteur est le double du premier coefficient. Lorsque l'ajustement
est bon, le coefficient de régression est très proche de
1. Comparez les résultats des 3 études et énoncez
vos conclusions.
Conclusions : L'étude de la chute libre
d'un point conduit aux observations suivantes :
Conseil : Le centre de gravité d'un triangle se trouve aux 2/3 de chaque médiane, à partir du sommet.
Sommaire : Travail
personnel, caractéristiques d'une force, poids d'un corps, poussée
d'Archimède, réaction d'un support, traction (tension) d'un
fil ou d'un câble, forces exercées par un ressort, effets
d'un force, équilibre d'un corps, faire un inventaire correct des
forces extérieures appliquées à un solide, travail
pratique : Le pèse-personne, le centre de gravité d'un solide,
rôle d'une poulie.
Comment tient une ventouse ? Si on colle la ventouse au support
tiendra-t-elle plus fort ?
Un agriculteur emploie une éolienne pour pomper de l'eau. Qu'est
ce qui la fait tourner, qu'est ce qui la freine, peut-elle tourner de plus
en plus vite, à n'importe quelle vitesse ?
Comment un sous-marin fait-il pour remonter à la surface ?
Pourquoi un satellite de la Terre ne se perd-il pas dans l'espace ?
// Veuillez noter qu'il n'est pas indispensable de
parler de force pour trouver une réponse aux questions précédentes.
Vous verrez par exemple, dans la leçon "Énergie potentielle",
traiter la chute des corps sans faire intervenir le poids de ceux-ci, mais
en introduisant une nouvelle forme de l'énergie, l'énergie
potentielle de pesanteur.
Le concept de force n'est pas indispensable pour résoudre
un problème de mécanique en physique, mais il est bien commode.
Une force peut être :
Une force de contact localisé, une force de contact
réparti, une force à distance.
Une force est caractérisée par :
Voici quelques exemples de forces courantes.
Chaque particule constituant un corps est soumise à
une force d'attraction gravitationnelle due à la Terre. Si le corps
est indéformable, l'ensemble de ces forces peut être
assimilé
à une force unique appelée
poids du corps.
Le poids est modélisé par un vecteur 
,
représenté par un segment fléché :
| P = m . g |
g vaut environ 9,81 N . kg-1, en France, au niveau de la mer.
Le poids est une force qui s'exerce à distance.
// Remarque : La valeur du poids est souvent appelée
poids. Le mot poids désigne donc à la fois la forcemodélisée
par un vecteur et la valeur P de cette force.
// Discussion : Si le corps est déformable, la simplification précédente est-elle possible ? Pouvez-vous tenir un boîtier de CD en équilibre sur un doigt ? Une feuille de papier ? Le contenu d'un verre d'eau ?
// Le poids d'un corps est légèrement différent de l'attraction gravitationnelle de la Terre sur ce corps ; en effet, la force gravitationnelle est étudiée dans le référentiel géocentrique et le poids dans le référentiel terrestre animé d'un mouvement de rotation par rapport au précédent.
// Le centre de gravité d'un corps est quasi confondu avec son centre d'inertie, mais il est (un tout petit peu) plus bas ; en effet, si deux particules du corps ont même masse, celle qui est plus proche de la Terre est légèrement plus attirée.
// Réponses : Il est clair que la feuille de papier se déforme, tout en restant en équilibre. Quant à l'eau !!!
Imaginons un corps (solide ou déformable) plongé,
totalement ou partiellement, dans un fluide au repos (eau, air...
). Le fluide exerce sur la surface immergée du corps un ensemble
de forces réparties, qui peut être assimilé à
une force unique, appelée poussée d'Archimède.
Cette poussée est :
Posons un corps sur un support. Le support exerce sur le corps des
forces microscopiques, réparties selon toute la surface de contact,
dont l'origine est l'interaction électromagnétique entre
atomes.
Simplifions le problème en envisageant un corps solide, de surface inférieure plane, reposant sur un support lui-même plan.
Si le solide, est en équilibre, l'ensemble des forces
réparties peut être assimilé à une force unique 
,
appelée réaction du support, directement opposée au
poids du solide, donc appliquée au point de la surface de contact
par lequel passe le support du poids du solide, ou encore situé
à la verticale du centre de gravité du solide.
// Remarquez que plus le support plan s'incline, plus le point d'application de la réaction du support se rapproche de l'avant du solide. Remarquez aussi que ce point d'application est à l'intérieur de la surface de contact selon laquelle sont exercées les forces de contact réparties.
Si le support n'est pas horizontal,
étant verticale n'est pas perpendiculaire au support ; elle peut
être décomposée en deux composantes,
= 
+ 
est la composante
normale, est
la composante
tangentielle., qui s'oppose au glissement
du solide vers le bas, est appelée
force de frottement.
// Cas où le plan est trop incliné : Pour que le solide reste en équilibre, il faudrait que la valeur de la force de frottement devienne très grande. Si cela n'est pas possible (support pas assez rugueux), le solide se met à glisser sur le plan.
// Cas où le solide a une hauteur grande par rapport à sa base : Pour qu'il reste en équilibre, il faudrait que le point d'application de la réaction du support dépasse l'avant du solide ; c'est évidemment impossible, le solide ne peut rester en équilibre, il bascule.
En ce cas, la réaction
du support est toujours perpendiculaire au support. Si le plan est incliné,
le solide ne peut pas rester en équilibre.
// Note : Les physiciens utilisent souvent
le mot "tension" d'un câble, mais cette expression souffre d'ambiguïté.
Imaginons un navire remorquant un pétrolier. Supposons pour simplifier
que le poids du câble est négligeable. Dans ce cas, le câble
peut être assimilé à un segment de droite. Étant
en équilibre (ou animé d'un mouvement rectiligne uniforme),
il est soumis en ses deux extrémités à deux forces
directement opposées qui ont donc la direction du câble :
la force de traction du pétrolier sur le câble et la force
de traction du remorqueur sur le câble. La première est directement
opposée à la force de traction 
du câble sur le pétrolier ; la deuxième est directement
opposée à la force de traction 
du
câble sur le remorqueur
La force de traction sur
le pétrolier a donc la direction du câble. La force de traction du
pétrolier (par l'intermédiaire du câble) sur le remorqueur,
directement opposée à a
donc la même valeur. C'est cette valeur que les physiciens appellent
tension du câble ; parfois aussi ils nomment la force,
tension.
Cette force de contact a pour origine l'interaction électromagnétique.
La force, appelée parfois tension du
ressort, exercée par un ressort sur un solide est dans un sens si
le ressort est étiré, dans l'autre s'il est comprimé.
Il s'agit d'une force de rappel, car elle est de sens contraire à
la déformation du ressort. La valeur de cette force est proportionnelle
à l'allongement du ressort.
| T = k . | l - l0 | |
// Remarques : k décrit bien la raideur plus ou moins grande du ressort. Si un ressort est remplacé par un plus raide, k augmente, donc il faut une traction T plus grande pour l'allonger de la même quantité.
// Cette relation sera algébrisée en classe de terminale.
// Cette relation, appelée loi de Hooke, n'est
vraie que pour certains types de ressorts (les plus courants il est vrai)
: ressorts formés d'un fil de diamètre constant, enroulé
en hélice de pas constant, sur un cylindre (diamètre constant
donc) et pas trop déformés.
L'industrie (automobile) fabrique des ressorts à
flexibilité variable (ou à constante de raideur k non constante
! ).
Une force peut :
Lorsqu'un solide soumis à deux forces est en équilibre
:
Lorsqu'un solide soumis à trois forces est en équilibre
:
Vous veillerez sur les schémas à ne pas confondre
les représentations des forces et celles des vitesses, car ces deux
grandeurs physiques ne sont pas de même nature.
Il faut bien se mettre dans la tête que se lancer dans la
résolution d'un problème de mécanique en ayant traité
de façon bâclée le point de départ (référentiel
et bilan des forces) est perdre son temps. Des hypothèses
fausses ne peuvent que conduire à des résultats faux.
Vous aurez parfois l'impression que sur ces points votre professeur
de physique se comporte comme un tortionnaire, mais c'est la physique elle-même
qui est tortionnaire : Elle interdit des calculs justes à partir
d'hypothèses fausses. Dura lex, sed lex.
Au lycée, le référentiel sera toujours choisi de manière à être galiléen ; il vous sera cependant demandé de préciser le référentiel que vous avez choisi.
L'expérience montre que lors de l'établissement du bilan des forces, les étudiants commettent de nombreuses erreurs.
Pour limiter les risque d'erreur, vous pouvez construire, ainsi
que vous y invite le document d'accompagnement de ces programmes de première
S, des diagrammes objets-interaction.
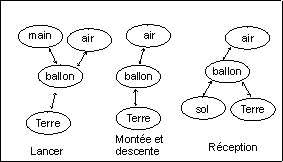
Voici un exemple concernant le lancer à la main d'un ballon qui retombe sur le sol. La différence entre les objets Terre et sol est celle-ci : Le sol exerce des forces de contact, la Terre (planète sur laquelle nous vivons) exerce une force gravitationnelle à distance.
Lors du mouvement du ballon, 4 phases peuvent être identifiées : Lancer, montée, descente, réception. Le bilan des forces est le même lors de la montée et de la descente ; seul le sens du vecteur vitesse change entre les deux. Ce point est important pour bien faire la distinction entre force et vitesse.
Page 76, exercices 1 (forces de contact ou à distance), 3
(révision élémentaire), 4 (loi de Hooke), 7 (solide
en équilibre sur un plan incliné), 8 (solide glissant sur
un plan incliné), 9 (somme de 2 forces), 13 (glaçon dans
un verre), 16 (pendule), 19 à regarder (équilibres d'une
brique sur un plan incliné).
Au bureau, 1 ou plusieurs pèse-personnes, autant de bâtons.
Rouleau de fil, ciseaux
Boîtes de masses marquées à crochet
Pour 9 groupes d'élèves :
2 pieds de physique
1 poulie sur tige
1 noix
1 crochet
1 masse à crochet de 100 g (ou autre)
1 ressort
1 règle graduée
1 fil à plomb
1 objet en carton ou contreplaqué
4.11.2. Fiche élève : Forces macroscopiques s'exerçant
sur un solide, expériences
Un élève tenant un bâton va monter sur un pèse-personne.
Il appuiera avec le bâton sur :
A l'aide d'un fil à plomb, déterminez la position
du centre de gravité d'un solide plan.
Comment pouvez-vous vérifier que vous avez trouvé la
position correcte ?
Suspendez une masse à un ressort et mesurez l'allongement
(vertical) de celui-ci.
Avec la même masse, étirez le ressort, cette fois à
l'horizontale, en vous aidant d'un fil et d'une poulie. Mesurez l'allongement
obtenu et comparez-le au précédent.
Faites un bilan des forces exercées sur la poulie. Ce bilan
devrait expliquer votre résultat expérimental.
// Note : Il sera plus facile pour établir
un bilan, la poulie étant immobile, d'imaginer que le fil est collé
à la poulie, aux deux points de contact extrêmes.
Sommaire : Travail personnel, principe de l'inertie,
deuxième loi de Newton, principe des actions mutuelles ou des interactions,
La physique d'Aristote (384-322 avant notre ère) indique
que :
C'est la première loi de Newton, vérifiée expérimentalement
et énoncée auparavant par Galilée.
Dans un référentiel galiléen, le
vecteur vitesse  du
centre d'inertie d'un solide est constant si et seulement si la somme vectorielle
des forces extérieures qui s'exercent sur le solide est nulle. |
Vecteur vitesse constant : Cela signifie, que si la vitesse est
nulle à un instant, elle reste nulle ; le solide est et reste au
repos (par rapport au référentiel). Si la vitesse n'est pas
nulle, elle ne change pas de valeur, ni de direction, ni de sens au cours
du temps ; le solide est animé d'un mouvement rectiligne uniforme.
Cela peut aussi s'énoncer : Le solide persévère
dans son état de repos ou de mouvement.
Somme vectorielle des forces extérieures nulle
: En fait, la somme des forces intérieures (exercées par
des parties de l'objet sur d'autres) est toujours nulle ; il n'y a donc
pas lieu d'en tenir compte. Il s'agit bien d'une somme vectorielle.
Cela peut aussi s'énoncer : Les forces extérieures se
compensent.
Remarquez la relation d'équivalence : Si la somme vectorielle des forces extérieures est nulle, alors le vecteur vitesse est constant ; et réciproquement, si le vecteur vitesse est constant, alors la somme vectorielle des forces extérieures est nulle.
Référentiel galiléen : Par définition, c'est un référentiel dans lequel la loi précédente est vraie.
Cela peut paraître une boutade, mais il n'en est rien.
Rappelons un contre exemple évoqué
par le savant russe Landau, prix Nobel, dans un de ses livres de vulgarisation
de la physique :
Vous avez pris place à bord d'un navire pour une
croisière. Le navire est à quai, vous vous installez dans
votre cabine (sans hublot). Le lustre de la cabine pend au bout de son
câble ; il est au repos, les forces qui lui sont appliquées
(poids et traction du point de suspension) se compensent ; tout paraît
normal.
Vous vous endormez. A votre réveil, le lustre
se balance. Qu'en concluez-vous ? Qu'un lustre soumis à des forces
qui se compensent est obligatoirement animé d'un mouvement de balancement
? Ou que votre référentiel, le bateau, n'a plus ses propriétés
initiales ? La réponse est ici évidente.
Bien sur, si un référentiel paraît galiléen, mais qu'un doute subsiste, seules des mesures de plus en plus précises permettront d'apporter une réponse.
Quelques référentiels galiléens :
| Dans un référentiel galiléen, la
somme vectorielle des forces qui s'exercent sur un solide a même
direction et même sens que la variation du vecteur vitesse du
centre d'inertie du solide. |
// Remarque : Vous verrez cette loi énoncée de manière plus complète et plus mathématique en terminale.
Application : une balle de ping pong, à laquelle aucun effet (mouvement de rotation) n'a été donné, rebondit sur une table en suivant une loi analogue à la loi de la réflexion en optique (même valeur de vitesse, direction symétrique par rapport à la normale à la table). En négligeant le poids de la balle, trouvez la direction de la force exercée par la table sur la balle. Le résultat est-il conforme à ce que vous avez vu dans la leçon précédente, au sujet de la réaction d'un support ?
C'est la troisième loi de Newton.
Si un corps A exerce sur un corps B une force  ,
alors B exerce sur A une force  directement
opposée. |
Ceci est vrai quel que soit le mouvement de A par rapport à B.
// Note : Un principe de physique est une propriété qu'on ne démontre pas, contrairement à un théorème. En mathématiques, on parle d'axiome et de théorème. Les principes sont donc le point de départ de la démonstration des théorèmes. Il existe d'autres façons de présenter la physique, où ce qui est appelé ici principe se démontre, donc devient un théorème, mais à partir d'hypothèses de départ différentes. Les relations de la physique sont appelées principes ou théorèmes en se basant sur une façon très traditionnelle d'enseigner la physique.
Application 1 : Vous êtes au départ d'un 100 mètres. Au signal, vous étendez votre jambe (droite ou gauche) et vous vous retrouvez propulsé vers l'avant. Quelle est la force responsable de ce changement de vitesse ? Représentez-la qualitativement. Pourriez-vous effectuer un tel départ sur une piste verglacée ? Pourquoi sur une piste normale (non verglacée ! ) faut-il des cales ou 'blocs de départ' ?
Application 2 : L'hélice (ou la turbine) d'un avion aspire de l'air à une certaine vitesse et le rejette vers l'arrière à une vitesse plus grande. Quelle est la force qui entraîne l'avion ?
Exercice : Un trépied de masse 2 kg repose sur le
sol. Calculez la valeur des forces exercées par le sol sur chaque
pied. Même question s'il s'agit d'un tabouret à 4 pieds.
Page 92, exercices 5 (référentiels galiléens), 8 représentez les forces appliquées (forces sur une automobile), 9 et 10 (même problème dans 2 référentiels), 13, 18, 21.
5.5.2. Fiche élève
Transférez les coordonnées des positions successives du
centre de gravité de la boule dans un tableur.
Conservez uniquement la cote de la boule, nommée z.
Dans la première partie de la chute, quel est le type du mouvement ? Faites un bilan des forces appliquées à la boule.
Procédez de même pour la dernière partie du mouvement. Quelle est la loi de Newton que vous venez de vérifier ?
Lorsqu'une boule de 7 centimètres de diamètre chute dans l'air, à partir d'une vitesse initiale nulle, les forces de frottement connaissent différents régimes. Pour une vitesse de chute comprise entre 0,011 et 42,8 m.s-1, le régime est tourbillonnaire libre et la force de frottement est donnée par la relation F = 1/2 Cx r S v2, où Cx est le coefficient aérodynamique de la boule (non dimensionné), r la masse volumique de l'air en kg . m-3, S la section de la boule en m2 et v sa vitesse en m . s-1. Trouvez la valeur de la force de frottement F lorsque la boule a atteint sa vitesse limite de chute dans l'air. Calculez le Cx de la boule.
Valeurs numériques : Masse volumique de l'air 1,2 kg .
m-3, masse de la boule en polystyrène expansé
5,81 g (masse
de l'air occupant le même volume que cette balle : 0,22 g), diamètre
de la boule 7,0 cm.
Transférez les coordonnées des positions successives du
centre de gravité du solide dans un tableur.
Faites un bilan des forces appliquées au solide.
Étudiez le mouvement selon l'horizontale (en projection sur un axe horizontal). Vous pouvez, dans un tableur, représenter la fonction qui à la date t fait correspondre la coordonnée horizontale x. Quel est le type de ce mouvement ? Cette constatation est-elle en accord avec le bilan des forces ?
Étudiez le mouvement selon la verticale. Vous pouvez représenter
la fonction qui à la date t fait correspondre la coordonnée
verticale y. Quel est le type de ce mouvement ? Cette constatation est-elle
en accord avec le bilan des forces ?
Quelle est la loi de Newton que vous venez de vérifier ?