| Les élèves :
Cabrera Kalou, Dodane Jean-Baptiste, Dumont Christophe, Roussillon Cyril, Zammouri Latifa, et leur professeur Jean-Michel Jussiaux. |
Note importante : Lors de recherches sur un autre thème d'Olympiades de la Physique (Aberration chromatique d'une lentille mince), nous avons découvert des informations supplémentaires. Sur Internet, recherchez Optique diffractive. |
Charger un exemplaire du mémoire, au format Word 95, compressé sous WinZip, auto extractible.
Les élèves ont choisi eux-mêmes le sujet, malgré
les mises en garde de leur professeur : Il n'est pas possible de réaliser
un hologramme classique (exposition, développement, séchage,
restitution) dans les conditions de présentation devant un Jury
car la durée de l'exposé est de 20 minutes, la présence
de public nécessite un minimum d'éclairage et le montage
est soumis aux vibrations de la salle.
La première partie du travail a consisté à rechercher des documents sur l'holographie (Internet, encyclopédie Universalis, laboratoire d'optique de la faculté des sciences de Besançon, laboratoire IGE à Belfort, entreprise Imasonic à Besançon).
Il en ressort que l'holographie n'est plus objet de recherche fondamentale, mais que de nombreux groupes essaient de la mettre au service de l'imagerie (médecine, recherche de défauts dans des matériaux). Plusieurs sites Internet expliquent comment réaliser un hologramme. Un site propose même de prêter le matériel nécessaire, hélas, il s'agit d'un site officiel au Canada ! Ah que voilà une bonne idée pour développer le goût des sciences chez les jeunes (canadiens).
Nous avons ensuite visité une entreprise, Imasonic,
qui fabrique des émetteurs récepteurs ultra sonores pour
l'imagerie médicale (mesure de la vitesse du sang par effet Doppler
et échographie), fonctionnant par impulsions à 1,5 MHz. Un
responsable, Monsieur Olivier Le Baron, nous a expliqué le fonctionnement
des transducteurs, les problèmes d'adaptation d'impédances,
entre l'émetteur et le milieu (corps humain), pour que le maximum
d'énergie soit transmise au milieu, et entre le générateur
électrique, d'impédance de sortie 50 ohms et l'émetteur
d'ultra sons. Plus beaucoup d'autres informations, sur l'impédance
acoustique, le transfert idéal, les émetteurs composites,
l'atténuation, la bande passante, les matériaux amortisseurs
à l'arrière du PZT, pour amortir les vibrations et raccourcir
la durée des impulsions (pulse), la lame lambda sur quatre d'impédance
intermédiaire qui favorise le transfert d'énergie vers l'avant
(comparable au traitement antireflet monocouche des lentilles en optique),
la distance de champ proche, le diamètre actif des émetteurs
qui ne sont pas tous plans, la technique de fabrication, dépôt
des électrodes, découpe, les caractéristiques des
pulses à appliquer (200 V, polarité négative sinon
le PZT peut être dépolarisé, récurrence 10 kHz,
puissance électrique 2 W).
Il nous a été remis 4 exemplaires d'émetteurs rejetés
au contrôle qualité. Mais nous ne sommes pas parvenus à
les faire fonctionner correctement. Ces émetteurs sont prévus
pour la transmission des ultra sons dans l'eau ; or nous souhaitons, pour
des raisons évidentes dictées par la nécessité
de présenter nos recherches en public, devant un jury, travailler
dans l'air. Nous n'avons donc pas insisté.
Les responsables d'Imasonic nous ont aussi donné l'adresse d'une
petite entreprise qui cherche à caractériser les défauts
à l'intérieur d'objets métalliques massifs, par holographie
ultrasonore : PRL, Corelec SA, 19, route nationale 77580 Crécy la
Chapelle, tél. 01 64 63 44 11, fax 01 64 63 69 75, contact : Jean-Michel
Hasquenoph.
Nous avons aussi visité le laboratoire d'optique de la faculté
des sciences de Besançon. Au musée de l'holographie (responsable
Claudine Bainier, tél. 03 81 66 64 21), nous avons obtenu des renseignements
sur la réalisation pratique d'un hologramme (exposés un peu
plus loin dans cette page), bien que le laboratoire d'optique n'en fabrique
plus.
Nous en avons profité pour examiner le fonctionnement de microscopes
optiques en champ proche. Ce qui nous a le plus surpris, c'est de voir
la lumière verte d'un laser changer progressivement de couleur en
progressant le long d'un fibre optique : L'effet Raman, utilisé
pour diminuer la cohérence de l'onde laser destinée à
éclairer les objets observés par le microscope. Les tables
anti vibratoires sur coussin d'air nous ont aussi étonné.
Nous avons obtenu d'autres informations :
Sur les plaques à holographie, Kodak a cessé d'en produire, Agfa n'en livre que par grandes quantités, ABSYS SA (voir plus loin) en fournit au détail. Une notice technique, en anglais, sur les compositions chimiques des révélateur et fixateur, nous a été photocopiée (voir traduction en français plus loin). La firme Leybold fournit films pour l'holographie et réactifs chimiques nécessaires.
Sur l'emploi de l'holographie : Un laboratoire de l'Université de Franche Comté pratique la mesure de vibrations par holographie, contacter Emmanuel Foltête, laboratoire de mécanique appliquée Chaléat, chemin de l'épitaphe 25030 Besançon, tél. secrétariat 03 81 66 60 03, salle de manipulations 03 81 66 67 27. Ils ont bénéficié d'un transfert de technologies du laboratoire d'optique. Un professeur des Beaux Arts (en retraite) a réalisé des hologrammes avec l'aide du laboratoire d'optique, Jean Gilles, rue Jean Wyrsh, 25000 Besançon. Le CREST réalise l'étude d'écoulements fluides dans les turbines, à l'aide de l'holographie, directeur Jean-Pierre Prenel (l'ancien binôme en licence et DEA d'optique de notre professeur J-M Jussiaux ! ), IGE Parc technologique (CREST), 2, avenue Jean Moulin 90000 Belfort. Mail : prenel@ige.univ-fcomte.fr
Nous avons contacté celui-ci, et voici sa réponse
:
| Bonjour
Comme le temps passe!! Holographie : ce n'est plus qu'un (bon) souvenir sur le plan de la recherche . Notre labo a quitté le domaine dans les années 80. Aujourd'hui , nous appliquons l'optique pour l'analyse quantitative des écoulements , des phénomènes thermiques ou des microsystèmes. Nous développons également des microcapteurs pour le tracé des profils énergétiques des faisceaux laser. Le labo ne dispose donc plus d'aucun matériel adapté à ton problème. Le seul "reliquat holographique" figure dans l' enseignement (DESS et surtout DEA). Désolé! Ceci dit , tu seras le bienvenu si tu souhaites visiter le labo! cordialement JP PRENEL |
La lumière est une onde (une vibration qui se propage)
électromagnétique. Comme toute onde elle a donc une fréquence
(elle vibre plus ou moins vite), une amplitude (plus ou moins de
lumière) et une phase ou terme de phase, plus précisément
(elle arrive plus ou moins en retard). Lorsque deux ondes se superposent,
elles interfèrent : Lorsque les vibrations arrivent en phase,
leur effet se renforce ; lorsqu’elles arrivent en opposition de phase,
leurs effets se contrarient.
Lors de la réalisation d’une photographie les différentes
ondes lumineuses qui frappent la plaque sensible à la lumière
ont des phases et des fréquences très variées : les
effets d’interférence se modifient très rapidement et la
plaque n’enregistre qu’un effet moyen.
La photographie n’enregistre que l’amplitude de l’onde lumineuse.
Pour pouvoir restituer une image en trois dimensions, il faut enregistrer à la fois l’amplitude et la phase de l’onde issue de l’objet. L’holographie y parvient par superposition de cette onde issue de l’objet lumineux et d’une onde de référence. Cela nécessite une lumière dont la fréquence et la phase sont très stables. L’hologramme est donc enregistré à l’aide d’un laser, sur un montage antivibratoire
Nous avons commandé des plaques à holographie chez
ABSYS S.A.
7, Rue Soddy
94044 Créteil Cedex
Tél. : 01 49 56 91 00, Fax : 01 49 56 91 62
Boîte de 20 plaques sensibles au rouge (633 nm) 2,5 x 2,5 pouces,
réf. 11 64 00 au prix de 433 F H.T. plus port.
Boîte de 25 plaques sensibles au rouge (633 nm) 4 x 5 pouces,
2200 F H.T..
En suivant les indications de la notice en anglais, The BB-Plates
: Notes for use, version : 02/97, nous avons ensuite commandé
chez Prolabo, les réactifs chimiques nécessaires au développement
et réalisé les bains de développement, de fixation.
Voici la traduction en français de la recette retenue :
// Note : Il est possible, en dépannage, d'employer
un révélateur du commerce, à fort contraste, type
D19, mais semble-t-il, livré uniquement par boîte de un kilogramme.
En ce cas, développer de 3 à 6 minutes.
700 cm3 d'eau, de préférence déionisée
70 g de carbonate de sodium anhydre
15 g d'hydroxyde de sodium *
4 g de métol
25 g d'acide ascorbique
Complétez avec de l'eau pour obtenir 1000 cm3
* Veuillez noter que certaines substances figurant dans la formule sont toxiques et / ou corrosives. Veuillez manipuler ces substances en respectant les règles de sécurité en vigueur dans votre pays.
// Note : Nous avons dû rechercher les autres noms du métol. Après quelques essais de lecture de plusieurs catalogues de fournisseurs de réactifs chimiques, longs et inefficaces, nous avons demandé le mot 'metol' au moteur de recherche Internet Metacrawler et la première réponse de Metacrawler a été la bonne ; elle comportait dans la description retenue pour un site, les synonymes, méthol et N-Méthyl-p-aminophénol sulfate, ou 4-(Methylamino) phenol sulfate, ou encore Méthylamino-4 phénol sulfate (Rhodol). Il n'a même pas été nécessaire de consulter le site proposé !
Veuillez attendre que chaque réactif soit dissout, avant d'ajouter le suivant sur la liste. Il est important de limiter le temps de contact de la surface du révélateur avec l'air (oxygène). Par conséquent, il est vivement recommandé d'employer deux cuvettes de développement en matière plastique, bien ajustées l'une à l'autre, la deuxième flottant sur la surface du révélateur. Le seul moment où la surface de celui-ci est exposée à l'air étant lorsqu'on surveille l'avancement du développement. Développez jusqu'à une densité d'au moins 2,5.
1000 cm3 d'eau, de préférence déionisée
5 g d'hydrogénosulfate de sodium * cristallisé (sodium
hydrogénosulfate, 1 molécule d'eau, Na H S O4,
H2 O)
Rincez brièvement dans de l'eau froide et fixez
700 cm3 d'eau, de préférence déionisée
35 g de sulfate de cuivre (pentahydraté) *
100 g de bromure de potassium
5 g d'hydrogénosulfate de sodium * cristallisé
Complétez avec de l'eau jusqu'à 1000 cm3
Fixez jusqu'à ce que l'hologramme soit transparent. Rincez dans de l'eau froide. Normalement, sauf si vous avez réalisé des matrices (reflection master holograms, en anglais) d'hologrammes en réflexion, le fixage doit toujours être suivi du passage dans un bain 'anti tirage' (//Note : il doit s'agir d'un traitement empêchant la reproduction de l'hologramme par tirage par contact) dont la composition est la suivante :
// Note : ce quatrième bain est facultatif pour ce
que nous avons à faire
700 cm3 d'eau, de préférence déionisée
3 g de dichromate de potassium *
6 g d'hydrogénosulfate de sodium *
Complétez avec de l'eau jusqu'à 1000 cm3
Traitez environ 1 minute en agitant. Pour rincer, plongez très
vite dans de l'eau déionisée ne contenant aucune trace de
révélateur. La brièveté du rinçage est
nécessaire pour qu'il reste un peu de solution anti tirage dans
le corps de l'hologramme. Notez que le dichromate de potassium est une
substance toxique et que les hologrammes traités, mais non protégés,
ne doivent pas être manipulés par de jeunes enfants.
Cet 'anti tirage' offre l'avantage supplémentaire de diminuer
une éventuelle coloration présente dans l'émulsion
du fait de la sensibilisation.
Remarquons encore une fois cette tentation du secret, de la non reproductibilité du travail.
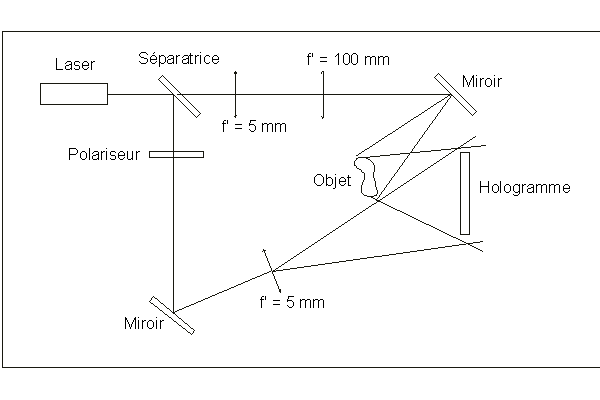
Le banc Leybold (Il n'est pas indispensable, mais bien pratique, car très rigide, assez lourd, et livré avec des supports magnétiques qui peuvent se poser où on le souhaite, voir paragraphe suivant) supportant le montage est posé, ainsi que nous l'avons vu conseillé sur des sites Internet, sur une chambre à air de remorque, pas trop gonflée, ce qui se révèle efficace contre les vibrations.
Pour déterminer le meilleur temps de pose, nous réalisons
une plaque test, avec des zones différemment exposées,
5, 10 et 20 secondes, en interposant sur le trajet de la lumière
un petit écran tenu à la main, sans toucher le montage, pour
éviter les vibrations.
Nous avons trouvé sur un site Internet des valeurs conseillées
de 4 s, ou un peu plus, pour un hologramme en réflexion et un laser
de 5 mW, 20 secondes pour un hologramme classique.
D'autres conseils ont été trouvés :
La première plaque (nous avons failli exposer un carton de
protection !) est exposée 5, 10 et 20 secondes (technique employant
un cache découvrant progressivement l'hologramme, en faisant attention
à ne rien toucher, pour ne pas créer de vibrations) avec
une diode laser de 3 mW dont le faisceau est étalé sur environ
8 x 4 cm ; elle est développée 2 minutes à 20 °C
; nous constatons qu'elle a noirci (densité grossièrement
estimée égale à moins de 1) ; elle est passée
30 secondes dans le bain d'arrêt, puis 2 minutes dans le fixateur.
Nous constatons qu'elle est devenue presque totalement transparente (ce
qui est prévu dans le mode d'emploi). Nous la laissons sécher
une minute (nous sommes impatients) et la plaçons dans le montage
de restitution. Nous n'observons rien !
Nous reprenons contact avec Claudine Bainier, qui par bonheur est immédiatement disponible. Elle nous indique que ce n'est pas facile ; qu'il faut s'assurer de la stabilité du montage en créant un interféromètre et en projetant les franges ; qu'il faut développer jusqu'à une densité de 2. La restitution ne doit pas se faire dans le rouge, mais dans le vert, car le fixage retire de la matière dans l'émulsion, et les franges d'interférences ne sont pas à la distance prévue ; il vaut mieux restituer en lumière blanche qu'avec un laser rouge.
Pendant ce temps, notre hologramme a continué à sécher, et a changé d'aspect. Nous l'éclairons en réflexion, avec une lampe de bureau à ampoule halogène basse tension, dotée d'un filament très petit, et surprise, sous une certaine incidence, nous voyons l'une des pièces de monnaie et une partie du papier d'aluminium froissé (de couleur rouge).
Nous en réalisons un deuxième ; exposition 12 secondes, développement 4 minutes, jusqu'à une densité beaucoup plus forte (2 ou 2,5 ?) (estimée en rinçant temporairement l'hologramme et en observant à travers, une des diodes électroluminescentes vertes). Après passage dans le bain d'arrêt, nous fixons une minute, mais l'hologramme est toujours opaque, puis deux minutes ; il s'éclaircit, mais reste assez sombre. Après séchage au sèche-cheveux, nous observons le restitution de deux pièces de monnaie, une bien visible, l'autre moins.
Notre montage est donc stable, nos réglages sont en gros corrects. Nous décidons d'améliorer la qualité du faisceau de notre diode laser, en enlevant sa lentille collimatrice et aussi l'objectif de microscope. Nous allons aussi modifier les glissières tenant l'hologramme qui coupent trop de lumière.
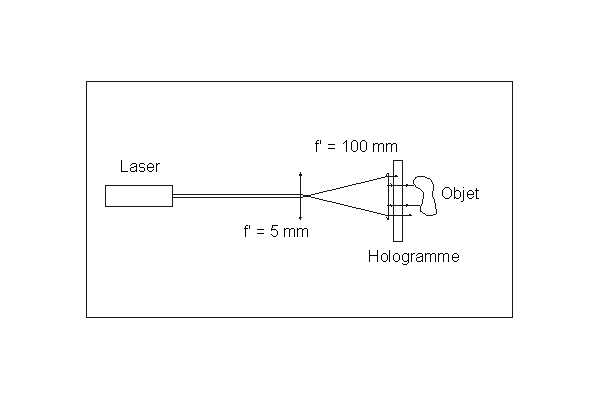
Nous avons emprunté à l'IUFM, un banc Leybold servant de support pour la réalisation d'hologrammes (Il n'est pas du tout indispensable, mais bien pratique tout de même). Dans un premier temps, nous l'avons employé pour restituer un hologramme possédé par le laboratoire du lycée, d'abord avec un laser, ensuite avec une diode laser. Il faut pour cela étaler le faisceau laser, à l'aide d'une lentille de courte distance focale (objectif de microscope) et d'une lentille de 10 ou 15 cm de focale. Nous allons simplifier encore le montage en enlevant la lentille collimatrice de la diode laser et l'objectif de microscope.
Nous avons essayé de changer l'angle d'incidence de l'onde plane éclairant l'hologramme, pour nous apercevoir qu'une variation de 10 ° ne modifiait pas la restitution. Nous avons ensuite retourné l'hologramme : L'objet restitué l'a été de l'autre côté du faisceau de référence. Nous avons ensuite tourné l'hologramme, pour constater que le faisceau de lumière restituant l'objet tournait en même temps.
Nous ne vous l'avions pas dit, mais depuis un certain temps, l'essentiel
de notre travail a consisté à tenter de créer des
hologrammes par calcul informatique. Nous avons trouvé beaucoup
de sites Internet traitant ce sujet et nous avons contacté certains
auteurs, nous avons aussi participé à des forums de discussion.
Pour cela, cherchez, à l'aide de Metacrawler,
les mots clés : Computer generated hologram ou Computer generated
holography ou cgh.
Nous avons obtenu une réponse charmante du directeur du M.I.T. nous disant qu'il fallait faire de la transformation de Fourier (FFT) en deux dimensions, que c'était comme en une dimension, mais avec deux dimensions et que notre professeur nous expliquerait tout cela.
Mais personne n'a accepté de nous donner du code source. Il semble que beaucoup de personnes travaillent encore sur le sujet, mais ne veulent rien communiquer. Parfois ils évoquent des résultats passionnants qu'ils ont trouvé, sans en dire plus et en même temps incitent ceux qui auraient des idées originales sur le sujet à les leur communiquer (les petits malins ! ). Certains indiquent qu'ils ont beaucoup de mal et que les résultats sont décevants (les plus sincères ? ).
Nous avons trouvé un logiciel, bridé (hologramme de 50 x 50 pixels) fonctionnant selon le processus suivant : Choix d'une figure simple, attribution d'une phase aléatoire entre 0 et 2 Pi radians à chaque point de la figure, calcul de la transformée de Fourier à deux dimensions, selon une méthode curieuse, puisque le calcul ne s'arrête que lorsqu'on le décide, la transformée évoluant d'abord rapidement au cours du temps, puis ensuite plus lentement. Rien n'est prévu pour imprimer l'hologramme obtenu à l'écran ; nous avons donc fait Impr écran et transféré l'hologramme minuscule dans un logiciel de dessin (Paint), pour l'imprimer. Mais le résultat n'a pas été concluant. Un autre logiciel a été testé, mais il donne l'hologramme sous la forme d'un fichier postscript qu'il faut ensuite traduire pour l'imprimer. Nous avons renoncé pour l'instant.
Nous avons alors, aidés par notre professeur, commencé
à rédiger notre propre programme. Les premiers résultats
ont donné de superbes figures sur l'écran de notre ordinateur,
avec plein de cercles se croisant dans tous les sens ; mais quant à
la restitution du sujet, rien de rien.
Nous avons alors simplifié le logiciel pour qu'il crée l'hologramme d'un seul point lumineux. Il a donné des disques alternativement rouges et noirs à l'écran, blancs et noirs sur le papier ou le transparent. Et merveille, ce Mercredi 11 Avril, non seulement le point a été restitué, mais de plus, l'hologramme s'est comporté comme une lentille convergente. Le montage de restitution peut donc être grandement simplifié. Par contre il y avait une grave erreur sur les distances (focales), environ 8 fois plus faibles que prévues. Le logiciel a été immédiatement revu. Les focales n'étaient plus que 2 fois trop faibles, mais surtout, nous avons pu restituer plusieurs points, formant une image très simple. Cependant, des points parasites brouillaient l'observation.
Conclusions provisoires : Les disques parasites sur l'hologramme et les points parasites à la restitution sont dus à des artefacts de calcul qui se produisent quand les franges d'interférence sont trop serrées par rapport à ce que peut rendre l'écran de l'ordinateur, ou l'imprimante. A ce sujet, l'imprimante Laserjet HP, donnée pour une résolution de 600 points par pouce (avec RET), semble plafonner à 300, car il y a plus d'artefacts sur le transparent imprimé que sur l'écran.
Pour réduire ces artefacts splendides, il faut éloigner le point source (imaginaire) de l'hologramme. Une autre méthode consiste à limiter (par le calcul) l'angle solide d'émission de lumière des points sources.
Il vous permettra d'étudier la diffraction, les interférences, le principe du retour inverse de la lumière, l'holographie et de réaliser à l'aide d'une imprimante des réseaux et des réseaux zonés de Fresnel.
Pendant que nous y sommes, indiquons que le calcul a été simplifié, à partir de renseignements obtenus sur Internet et confirmés par nos propres calculs. Il est inutile d'ajouter une onde de référence aux ondes émises par les points sources. Il suffit d'ajouter toutes les parties réelles des contributions des différents points lumineux, et de normaliser le résultat, c'est à dire d'ajouter à chaque valeur réelle trouvée un nombre permettant de n'obtenir que des résultats positifs (minima voisins de zéro), et de multiplier le tout par un coefficient tel que le maximum soit de 255 pour l'écran et de 1 pour l'imprimante. Pour imprimer, tout cela peut être encore simplifié, car finalement l'imprimante ne connaît que deux valeurs, 0 (point noir) ou 1 (point blanc). Nous pouvons donc nous contenter du test : partie réelle négative ou nulle -> noir ; positive -> blanc.
Si les franges d'interférences sont trop serrées, il apparaît des artefacts splendides (des anneaux partout) qui à la restitution créent des points parasites. Cela est dû à un échantillonnage insuffisant. Ce phénomène est moins visible en niveaux de gris qu'en noir et blanc.
A partir d'un objet imaginaire, il s'agit de calculer point par
point l'éclairement au niveau de l'hologramme, d'imprimer le tout
sur un transparent, puis de procéder à la restitution.
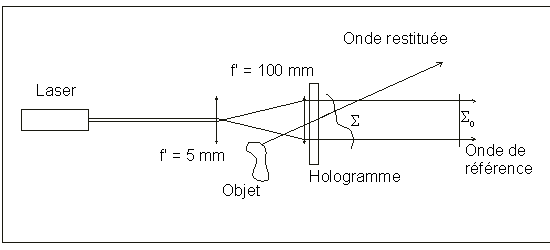
En fait, les calculs peuvent être simplifiés : Il n’est
pas nécessaire de calculer la superposition des ondes S
et S0, mais seulement l’amplitude
de l’onde S, sans son terme en j w
t. En effet, si la transmittance de l’hologramme transparent calculé
puis imprimé est proportionnelle (en fait, affine) à A cosf
, l’onde émergent de cet hologramme éclairé par l’onde
de référence A cos (w t)
est : A cos (w t) A cosf,
soit 1/2 (A0 A) [cos(w t +
f) A cos(w t - f)
].
A une constante multiplicative près, le premier terme est l’onde
S.
Si l’objet est un point lumineux, le premier terme restitue celui-ci, donc
un point situé à distance finie, avant l’hologramme, qui
pourra être observé en regardant dans l’hologramme, avec le
risque de se brûler les yeux ; il sera aussi possible de former l’image
de ce point sur un écran, à l’aide d’une lentille convergente
de 2 dioptries, placée contre l’hologramme. Mais il y a encore plus
simple, puisque le deuxième terme est une onde convergente. L’hologramme
se comporte alors comme une lentille à la fois convergente et divergente.
Mais de sérieuses difficultés surgissent :
La finesse des franges est limitée par les capacités de
l'imprimante. Avec une LaserJet de résolution 600 points par pouce,
l'angle entre les ondes S et S0
est de 0,4 °. La restitution est donc délicate, avec le risque
de recevoir dans l'œil les deux faisceaux à la fois. Certains auteurs
sur Internet proposent donc d'imprimer l'hologramme, puis de le photographier
en réduction sur microfilm, pour resserrer les franges d'interférence,
mais cela nous écarte de notre objectif qui est de calculer un hologramme
justement pour ne pas avoir à attendre à cause d'un processus
chimique. Nous verrons que nous avons réussi à contourner
cette difficulté en calculant des hologrammes convergents, donnant
des images réelles. Celles-ci apparaissent comme des points lumineux
dans le faisceau de référence qui est une onde plane étalée
; un simple écran permet donc de les observer, sans risque d'éblouissement.
Il est même possible de calculer un hologramme dont la plus grande
partie de la surface est noire, ce qui atténue d'autant l'onde de
référence.
Qui plus est, la taille de ces hologrammes convergents n'est pas limitée,
si lors du calcul on limite l'angle solide d'émission de lumière
de chaque point lumineux ! Nous avons retenu des hologrammes de 600 x 600
pixels, soit 1 pouce carré, soit encore 25 x 25 mm, pour notre montage
de restitution dont la deuxième lentille de marque Leybold a une
distance focale de 15 cm, pour un diamètre de 8 cm. Notre laserJet
ayant une mémoire de 500 kilo octets, cela représente 500000
x 8 = 4000000 pixels soit une taille maximale de 2000 x 2000 pixels, soit
83 x 83 mm. Au-delà, la mémoire 'explose', ce qui produit
un plantage de l'ordinateur. Par contre, pour des hologrammes aussi grands,
les aberrations géométriques de la deuxième lentille,
chargée de créer une onde plane étalée, apparaissent
et tous les points objets lumineux (imaginaires) situés dans un
même plan ne donnent pas des faisceaux lumineux convergeant dans
un même plan ; de belles aberrations apparaissent sur les bords,
coma...
La deuxième difficulté tient au fait que l'imprimante
ne connaît que deux 'couleurs', blanc ou transparent et noir. Il
est impossible d'utiliser des nuances de gris que l'imprimante réalise
par un tramage noir et blanc, ce qui au niveau de la diffraction doit être
amusant. Il faudrait une imprimante jet d'encre injectant des encres plus
ou moins diluées et qui n'existe pas à notre connaissance.
Nous devons donc arrondir sauvagement les résultats de nos calculs.
Le plus simple est de décider :
Partie réelle du résultat calculé négative
ou nulle -> noir et partie réelle positive -> blanc ou transparent.
La troisième difficulté tient au temps de calcul. Supposons
que notre objet ait une taille de 600 x 600 pixels ; il comporte donc 360000
points. L'hologramme est choisi de même taille. Pour chaque point
calculé de l'hologramme, il faut tenir compte de la contribution
de chacun des points de l'objet, soit 360000 x 360000 calculs, chaque calcul
comportant une recherche de distance parcourue par le rayon lumineux ;
soit donc 130 milliards de calculs. Si chaque calcul consomme 50 cycles
d'horloge, cela donne près de 1013 cycles soit 64800
secondes pour un processeur tournant à 100 MHz, soit encore 18 heures.
Même avec le meilleur ordinateur de notre laboratoire de physique,
nous ne pouvons atteindre l'objectif fixé d'une présentation
en 20 minutes.
Pour tourner cette difficulté, une hypothèse simplificatrice
est de dire que l'hologramme s'obtient à partir de la transformée
de Fourier (en deux dimensions) de la répartition d'amplitude dans
l'objet lumineux imaginaire. Les physiciens savent faire des transformées
accélérées, ou FFT ; mais il nous faut nous plonger
dans la FFT en 2 dimensions.
Nous avons retenu une autre solution : Nous envisageons un objet formé
d'un nombre restreint de points lumineux. Si par exemple l'objet comporte
100 points, la durée de calcul sera ramenée à 100
x 360000 x 50 soit 1,8 milliards de cycles, soit 18 secondes, ce qui est
raisonnable.
Dans le même ordre d'idées, nous avons envisagé
de construire un objet à l'aide de pavés lumineux. La contribution
d'un pavé se déduit de celle du point constituant son sommet
en haut à gauche, par deux séries géométriques
successives, donc un calcul à peine plus long que celui nécessité
par un point lumineux. Mais pour l'instant, nous avons un problème
à la restitution : Nous ne voyons apparaître que les quatre
coins du pavé. Cela est dû au fait que la figure d'interférences
sur l'hologramme est d'amplitude très variable et que notre imprimante
est incapable avec son noir et blanc de restituer quelque chose de correct.
Il s'inspire du précédent, mais le positionnement
des points se fait de manière graphique, l'état d'avancement
des calculs est affiché et il est plus élégant au
niveau de la programmation, utilisant plus la notion d'objet du langage
Pascal.
Le télé charger avec son code source ?
Ce sera notre dernière série d'expérience.
Il s'agit de remplacer les sources de lumière cohérente par
des sources d'ultra sons, d'enregistrer dans un plan les signaux reçus,
amplitude et terme de phase, de mémoriser les valeurs, d'imprimer
un transparent reproduisant de façon approchée cette répartition,
et de restituer le transparent. La principale difficulté consiste
à déplacer correctement le capteur et à connaître
avec précision la position de chaque point enregistré. Nous
ne savons pas si nous y parviendrons, autrement qu'en déplaçant
le capteur à la main.
Holographie par ultrasons : Émetteur à 40 kHz, alimenté
par un générateur basse fréquence, le faisceau se
réfléchit sur
un objet, il est reçu par un récepteur à 40 kHz
(identique à l'émetteur). Les parasites sont filtrés
par une résistance de
10 kilo ohms, montée en parallèle avec le récepteur.
Le signal reçu est envoyé sur une voie d'un oscilloscope
numérique
; sur l'autre voie, nous envoyons la tension de sortie du GBF, qui
sert de référence. Le sommateur de l'oscilloscope
remplace l'interférence entre l'onde utile et l'onde de référence.
En déplaçant le récepteur, on observe un signal à
40
kHz, dont l'amplitude varie. Il reste à balayer un plan, à
enregistrer cette amplitude en chaque point et à la transformer
en points noir et blanc sur un transparent.
Une difficulté technique qui reste à résoudre est
de contrôler le balayage du récepteur d’ultra sons, tout en
enregistrant son signal. Notre carte Candibus n’est capable que de donner
des valeurs logiques en sortie, pas des tensions. Un point lumineux peut
ici être simplement remplacé par un émetteur de petite
taille ; en raccordant plusieurs émetteurs au même générateur
basse fréquence, il est facile de réaliser des sources synchrones.
Il reste à trouver la correspondance entre le travail en lumière
visible et en ultra sons, car les longueurs d’ondes sont très différentes,
633 nm pour le laser et 8,5 mm pour les ultra sons, soit 13 000 fois plus.
Mais lors de l’impression d’un hologramme transparent, nous pouvons choisir
l’échelle de reproduction.
Mais faute de temps, nous ne pourrons poursuivre nos essais. Le plus
difficile étant de concevoir un système fiable de déplacement
du récepteur ultra sonore. L’idéal étant évidemment
de recevoir le signal sur une matrice de récepteurs.
Cette société a répondu très vite à
notre demande de renseignements, nous fournissant un dossier très
complet.
Elle conçoit des systèmes ultrasonores capables d’analyser
les défauts dans des pièces massives, par holographie. Tous
les éléments d’une sonde multi éléments d’échographie
classique travaillent à l’émission, mais aussi à la
réception, de façon indépendante. A chaque élément
est associée une mémoire. Un circuit de calcul spécialisé
traite ensuite les informations contenues dans les mémoires. Il
est très rapide puisque l’image d’une surface de 100 x 100 mm, correspondant
à une matrice de 200 x 200 capteurs, est calculée en 1/1000
de seconde.
Les avantages par rapport à l’échographie traditionnelle
sont :
· un gain important en rapidité (l’objet est analysé
globalement et non plus point par point), par exemple un rail peut être
analysé a une vitesse théorique de 360 km/h et à 100
km/h en pratique,
· un gain en sensibilité (car tous les éléments
sont employés en réception), des défauts de
0,05 mm sont détectés avec un rapport signal sur bruit de
30 dB,
· en fiabilité (si quelques éléments ne
répondent plus, cela affecte peu l’image obtenue),
· et une zone morte sous la surface (dans laquelle se mélangent
les ondes réfléchies et la traînée de l’onde
émise) plus faible (1 millimètre).
A l’heure actuelle, la solution couramment retenue n’est pas l’holographie,
mais la tomographie ; l’objet est analysé tranche par tranche et
l’image 3 D est reconstituée de manière informatique. Mais
des lasers X sont en train d’apparaître et modifieront peut-être
l’approche de l’imagerie.
Nous vous exposerons oralement ce que chacun d’entre nous a trouvé
sur ce sujet.
Quelques questions posées par le Jury, à Paris :
Vous avez montré un transparent présentant un agrandissement d'un hologramme. L'avez-vous réalisé vous-mêmes ? Comment a-t-il été réalisé ? Avec quel type de microscope ? Quel est l'angle d'incidence du faisceau de référence (imaginaire) dans vos hologrammes calculés ? Vous envisagez la réalisation future d'hologrammes par rayons X, avez-vous une idée de la finesse des franges d'interférence ainsi obtenues ? Vous dites que les grains de l'émulsion photographique permettant de réaliser un hologramme doivent être très fins. Avez-vous une idée de cette finesse ? Quelle influence cela a-t-il sur la sensibilité de l'émulsion ?
Suggestion d'un visiteur de l'exposition qui a suivi le concours
: Pour les hologrammes restitués en réflexion, la restitution
est meilleure si on projette au dos de l'hologramme de la peinture aluminium
en bombe (non essayé par nous).
Le groupe (formé à la fin de Donzé Sabine et de Richard Céline) à terminé un montage permettant de mesurer les oscillations d'une maquette de coque de navire et de les enregistrer avec un ordinateur. Pour cela, deux électrodes sont fixées sur la coque, une de côté et une au milieu et un montage de conductimétrie préalablement étalonné permet de connaître la hauteur de l'électrode latérale, au-dessus de l'électrode placée au fond du bassin de carène (ou plutôt de la bassine de carène).
Les paramètres influant sur la période d'oscillation sont étudiés : Forme de la coque, masse totale, répartition des masses longitudinalement et latéralement, hauteur du centre de gravité.
Cela permet de découvrir le métacentre, et de mesurer sa position, comparée au résultat calculé.
La présentation se termine par une démonstration sur les effets d'une carène liquide sur la stabilité d'un navire : Une masse d'eau est d'abord placée assez haut, mais limitée dans ses mouvements (en fait un simple verre) ; puis la même quantité d'eau est placée plus bas, mais libre de se déplacer dans la coque du navire. Dans ce deuxième cas, celui-ci chavire.
Quelques questions posées par le Jury, à Paris :
Connaissez-vous la fréquence des vagues ? La fréquence des oscillations d'un voilier monocoque et d'un catamaran est-elle la même ? Quel est l'effet d'un cloisonnement à l'intérieur d'un navire ?