hologramme, le miroir, remarque
importante, la loupe, la lentille
convergente, remarque
importante, la lunette astronomique, historique
,
l'œil humain ; leçons 1,
2,
3, 4, 5,
6 ; travaux pratiques
1,
2
hologramme, le miroir, remarque
importante, la loupe, la lentille
convergente, remarque
importante, la lunette astronomique, historique
,
l'œil humain ; leçons 1,
2,
3, 4, 5,
6 ; travaux pratiques
1,
2,
afin de les distinguer des propositions du document d'accompagnement des
nouveaux programmes de 1° S. La partie travaux pratiques est presque
complète, elle reste cependant à organiser pour que chaque
séance soit de longueur correcte, mais le cours est insuffisant.
Il est complet dans les paragraphes 15 à
18 qui suivent cette première approche.
Note : Les protocoles expérimentaux sont décrits dans le détail ; ils ne sont pas forcément à donner tels aux élèves. Souvent, il peut être plus profitable de demander aux élèves l'élaboration de leur propre protocole. Ceux qui figurent sur cette page deviennent alors un guide de préparation pour le professeur, ou un exemple de corrigé, ou le moyen de réaliser des expériences par soi-même.
Commençons par quelques généralités,
permettant de mieux comprendre comment le nouveau programme d'optique de
première peut enrichir celui de spécialité
physique de terminale S, et réciproquement. Vous trouverez à
la fin de cette page des compléments d'information sur l'histoire
de l'optique, sur l'œil humain
Qu'apporte de nouveau la façon de traiter ce programme d'optique, telle que préconisée dans les documents d'accompagnement ?
D'abord une réflexion simple sur ce que signifie voir une image.
Puis une approche expérimentale différente (et complémentaire de l'approche plus traditionnelle).
Les méthodes proposées en première S sont aussi
plus performantes que celle de spécialité physique,
chaque fois qu'il faut étudier une image virtuelle (ce terme
est à écarter dans l'enseignement de première), car
il est inutile d'employer une modélisation d'œil accommodant à
une distance finie ou infinie. Elles sont donc très intéressantes
(en terminale S option de spécialité) pour l'étude
des lentilles divergentes ou de la loupe. Par contre, elles sont moins
rapides que l'utilisation d'un écran pour l'étude des images
réelles.
Mais le programme de première fait remarquer à juste
titre qu'un écran permet de situer la position d'une image, trouver
sa taille, mais que diffusant les rayons de lumière qui forment
cette image, il ne permet pas en réalité son observation.
Pensez à l'étude en option de spécialité de terminale S, de l'image virtuelle donnée par une loupe (ou une lentille divergente), reprise par un modèle d'œil, qui donne sur son écran rétine, une image inversée (quand on regarde du bon côté de la rétine) donc droite puisque le cerveau lui-même retourne l'image. Ouf ! Alors qu'il suffit de regarder dans la loupe pour voir ce qui se passe ! Et que cette page internet montre comment situer l'image (virtuelle ici) avec une bonne précision et mesurer sa taille. La démarche est donc finalement plus naturelle et bien aussi efficace.
A ce sujet, vous trouverez dans ce chapitre un TP de terminale S spécialité physique, combinant les trois approches expérimentales (lentilles sur tableau magnétique, écran sur banc d'optique et réticule), pour l'étude des lois de conjugaison.
Il serait dommage de passer à côté, en se cantonnant aux travaux pratiques traditionnels ; sans rejeter tout ce qu'il y a de bon dans ceux-ci.
Remarque : Les premiers livres qu'il m'a été donné de consulter, reprennent pour l'étude des lentilles convergentes les méthodes classiques avec lettre lumineuse sur banc d'optique. Dommage.
Une liste de matériel dont l'acquisition pourra être utile :
10 miroirs rectangulaires protégés par un cadre
en matière plastique, tels que les miroirs à main en usage
dans les salles de bains,
10 lentilles de 8 ou 10 dioptries. Les lentilles, serties sous plastique
employées en spécialité physique de terminale S peuvent
convenir, mais il y a risque de télescopages entre les différents
travaux pratiques. Sous la marque Maped, on trouve des loupes peu
coûteuses, en verre, serties dans une poignée en matière
plastique. Deux diamètres sont disponibles, 50 mm (qui convient
parfaitement) et 75 mm. 10 lampes de bureau équipées d'ampoules
de faible puissance (lampes de réfrigérateur), ou des bougies,
10 lampes de bureau équipées de lampes de réfrigérateur
à petite vis, 15 W, 230 - 240 V, X9F,
des épingles à grosse tête,
des cartes de visite.
L'identification et la localisation des images sont effectuées
en observant de préférence des objets diffusants éclairés.
Les travaux pratiques se font généralement en plein jour,
la lumière utilisée étant celle du Soleil ou de l'éclairage
artificiel de la salle.
La démarche suivie pour étudier l'image donnée
par un système optique est toujours la même : Localisation
de l'image (par visées utilisant la parallaxe, ou par emploi de
réticules), recherche du chemin effectivement suivi par la lumière,
modélisation par construction des rayons lumineux sur une représentation.
Notons dès à présent que cette expression même
de rayons lumineux est ambiguë, puisqu'elle signifie trajet suivi
par la lumière et non pas rayon que l'œil voit.
Voici la définition donnée par le nouveau programme
de première scientifique :
L'image est l'interprétation du signal reçu par l'œil, effectuée par le cerveau conditionné à la propagation rectiligne de la lumière.
A comparer à celle du bientôt ancien programme de spécialité physique de terminale S, définition qui ne s'applique pas aux images de synthèse, pourtant fondamentales dans notre société.
Pour aborder ce point, il faut se poser les questions suivantes
: Qu'est-ce qu'une image ? Que signifie voir ? Qu'est-ce qu'un objet ?
Le lecteur pourra consulter avec profit dans le BUP N° 823,
d'Avril 2000, l'article 'Optique au collège : Le rôle de la
lumière dans la formation d'image par une lentille convergente'
qui analyse les idées fausses des élèves sur la lumière
et leur évolution en fonction de l'enseignement qui leur est fait.
Le document d'accompagnement (projet) physique propose, page 26 une
activité 1, situation 1. Quelles seraient les réponses des
élèves ? Je l'ignore et il faudra tester cela.
La manipulation est une variante du corps noir, une boîte percée
d'un trou, à l'intérieur peint en noir, dans laquelle est
placée une lampe non visible directement de l'extérieur.
On ne voit rien depuis l'extérieur, lorsqu'on ouvre le trou ! Étant
donné qu'il n'en sort pas de lumière, cela paraît naturel.
Cela revient à faire la deuxième expérience, avec
le laser, pour montrer qu'on ne voit pas un rayon lumineux, si celui-ci
passe devant nous. Mais ce qui paraît évident pour un professeur
de physique ne l'est peut-être pas pour un élève.
Je propose, si le temps est suffisant et si les réponses des élèves
ont dans l'ensemble été correctes, les variantes suivantes,
d'interprétation plus complexe, mais soulignant le rôle d'interprétation
du cerveau : Et si l'intérieur de la boîte est peint en blanc
? Et si la boîte est chauffée au rouge ? Voit-on quelque chose
depuis l'extérieur en ce cas ?
Je crois que oui ! Mais que voit-on ? Que signifie voir ?
Dans ces cas, les deux yeux de l'observateur ont une sensation lumineuse
; mais, si le trou est petit, chaque œil ne voit pas le même morceau
de la paroi lumineuse, et si la surface est uniforme, il n'est pas facile
au cerveau d'interpréter les sensations lumineuses. Si la paroi
intérieure éclairée ou rayonnante vue par les deux
yeux est sans détail, notre cerveau ne pouvant situer avec précision
l'emplacement de l'image verra un disque lumineux, au niveau du trou dans
la boîte, alors que la paroi est plus loin ; l'image semblera ce
disque. Si la paroi comporte des détails, nous verrons peut-être
(si nos deux yeux peuvent observer une zone commune) qu'ils sont situés
derrière l'ouverture dans la boîte.
C'est ce qui se passe la nuit lorsqu'on voit les fenêtres 'éclairées'
d'un immeuble lointain. Du fait de la distance, les détails du mur
du fond de la pièce ne sont pas discernables, de plus notre vision
stéréoscopique n'est pas assez précise pour nous indiquer
que le mur du fond est plus loin que la fenêtre ; notre cerveau ne
peut pas situer le mur ; par contre, le cadre de la fenêtre est très
contrasté. Notre cerveau interprète cela ainsi : Nous voyons
la fenêtre éclairée, ce qui est faux, puisque la vitre
n'est pas diffusante. Dans le langage de la vie courante, nous dirons même
que nous voyons de la lumière à la fenêtre.
C'est encore une erreur.
Un laser (ou une diode laser) est présenté aux élèves,
éteint, orienté vers un mur. On leur demande d'imaginer ce
qu'ils vont voir lorsque le laser sera mis en marche.
Il est possible que les élèves prévoient d'observer
un pinceau rectiligne de lumière sortant du laser.
Observation : On ne voit pas le faisceau du laser, mais uniquement une tache lumineuse sur le mur ; on peut aussi dire qu'on voit un objet, un petit fragment du mur, éclairé par le laser. Ce pourra être l'occasion d'évoquer les lasers utilisés dans les spectacles, ou les faisceaux de lumière signalant à distance la présence d'un lieu de divertissement nocturne : dans ce cas la lumière est diffusée par les poussières et gouttelettes d'eau présentes dans l'air ; cela se remarque bien quand le faisceau rencontre un nuage.
Nous pouvons observer ce qui se passe avec un modèle d'œil, ou avec
un œil de bœuf découpé au scalpel (berk ! ). Mais notre œil
à nous ? Comment voit-il ?
Consultez aussi l'ouvrage : Terminales S, Physique Spécialité, Ellipses, par l'auteur de ce site Internet, J-M Jussiaux.
Ce travail pratique peut être proposé aux élèves,
pour un travail personnel, chez eux.
Dans une feuille d’aluminium ménager, réalisez un petit
trou à l’aide d’une aiguille. Observez à travers ce trou
des objets éloignés puis très proches. Que constatez-vous
?
// Réponse : les objets paraissent moins
nets qu’à l’œil nu car le trou diffracte plus que la pupille de
l’œil. La profondeur de champ est très grande car le diaphragme
est très fermé. Essayez avec des trous de différents
diamètres. Les plus lumineux sont ceux dont les diamètres
sont les plus grands.
Regardez à travers le sténopé de l’expérimentation
n°1 6 1, une source de lumière de grande dimension. Par exemple
le ciel ou une feuille de papier éclairée par votre lampe
de bureau. Faites passer entre la source de lumière et le petit
trou un objet de petite taille, un cheveu, ou la pointe d'un crayon par
exemple. Tout se passe de façon habituelle. Faites passer maintenant
la pointe du crayon entre le trou et votre œil. Observez le sens de déplacement
de l’ombre du cheveu.
Faites un croquis pour comprendre ce qui se produit. Le cheveu est
tellement proche de l’œil que la convergence de celui-ci est négligeable.
Vous pouvez raisonner en terme d’ombres portées.
// Conclusion : les images sur la rétine sont renversées. Remarquez que dans cette manipulation, notre cerveau analyse le signal donné par l'œil à deux niveaux. Le premier, automatique : L'image est l'interprétation du signal reçu par l'œil, effectuée par le cerveau conditionné à la propagation rectiligne de la lumière, et nous voyons une ombre passer, à l'envers ; parfois même, nous voyons la pointe de crayon, à l'envers, se déplaçant à l'envers et semblant de l'autre côté du sténopé. Le deuxième nécessite du temps, de la réflexion (intellectuelle) et une feuille de papier pour tracer un schéma.
Observez toujours, comme dans l’expérimentation n° 2, une source
de lumière étendue à travers un petit trou. Le cercle
brillant que vous voyez est à peu de choses près la projection
de votre pupille sur la rétine. Avec l’autre œil, regardez la source
de lumière ; vos deux pupilles se contractent. Cachez lui maintenant
la lumière avec votre main. Les deux pupilles se dilatent. Évaluez
le temps de réaction.
Vous trouverez sur ce site, en télé chargement gratuit, un
logiciel permettant le calcul
de l'hologramme d'un objet lumineux (imaginaire) simple, pour l'instant
formé de deux fois huit points placés dans deux plans différents.
L'hologramme (convergent) imprimé sur transparent peut être
restitué, à l'aide d'un faisceau laser étalé
par deux objectifs convergents. Une diode laser convient aussi. Les points
lumineux sont visibles sur un écran ; ils pourraient être
observés sans écran, mais avec le risque de se brûler
la rétine. Ce logiciel réalisé dans le cadre des Olympiades
de la Physique est livré avec son code source turbo Pascal pour
Delphi de Inprise Borland et un fichier explicatif au format .pdf, consultable
à l'aide d'Adobe Acrobat.
L'onde restituée et l'onde de référence ne sont séparées que d'un angle de 0,4 °, à cause de la faible résolution (600 points par pouce) de l'imprimante. Une observation directe de l'image restituée, en plaçant l'œil dans le faisceau émergent, est donc dangereuse. Il faut par mesure de sécurité employer un écran, ou ajouter une lentille convergente et éliminer par un obstacle l'image ponctuelle de la source laser. Cela nous écarte donc de l'objectif d'observation directe des images affirmé dans ce programme de première S.
Un hologramme classique pourrait être plus intéressant : La restitution de l'onde qui provenait d'un objet, induit notre cerveau à voir cet objet.
Un objet est placé derrière un écran percé
d'une fenêtre rectangulaire. Où doit-on placer l'œil pour
voir l'objet complètement, partiellement ou pas du tout ?
Il semble que cette question fait apparaître beaucoup d'idées
fausses chez les élèves.
C'est l'occasion de réinvestir ce qui a été
vu en classe de seconde, pour mesurer la distance d'un objet inaccessible,
par la méthode de la parallaxe.
Ceci est une introduction au travail pratique suivant.
Les élèves doivent proposer une méthode de travail.
Matériel nécessaire : Une planche à dessin, une grande feuille de papier, des épingles, un objet (par exemple un stylo), un cristallisoir.
Protocole que les élèves pourraient proposer : Placez l'objet sur la feuille de papier, en repérant sa position. Posez dessus le cristallisoir. Repérez en plantant des épingles deux directions conduisant à l'objet. Enlevez le cristallisoir et vérifiez la précision des tracés.
Une équerre convient tout aussi bien, mais les réticules
peuvent être laissés en place.
Protocole : Placez d'abord l'objet en face du miroir.
Choisissez dans cet objet un point P, appelé point-objet, par
exemple la pointe du stylo. Sur la feuille de papier, inscrivez les position
et dimension du miroir, ainsi que la position du point P.
Notre cerveau, lorsqu'il interprète l'information qui lui
provient de l'œil, est conditionné à la propagation rectiligne
de la lumière. Pour lui, tout se passe comme si la lumière
provenait directement du point P', symétrique de P par rapport au
miroir.
Le point P' est appelé point-image conjugué du point-objet
P.
Si on considère l'objet comme un ensemble de points-objets,
à chaque point-objet correspond un point-image. L'ensemble des points-images
est appelé image de l'objet.
|
Lors d'une réflexion sur un miroir plan, les rayons incident
et réfléchi sont dans le plan d'incidence.
|
Y a-t-il encore un point-image P' si le point-objet P n'est plus
en face du miroir. Si oui, le situer et déterminer la zone de visibilité
de ce point.
| A tout rayon (appelé rayon incident) issu d'un point-objet
P, qui rencontre la surface du miroir en un point S, est associé
un rayon unique appelé rayon réfléchi vérifiant
les lois de la réflexion.
On appelle point-image P' du point-objet P, donné par le miroir, le point P' de rencontre des prolongement des rayons réfléchis. Les points image P', et objet P, sont appelés points conjugués et sont symétriques par rapport au plan du miroir. |
| Conditions de visibilité d'un point-objet à travers
un miroir plan :
Un point-objet P sera vu dans le miroir par l'œil O de l'observateur si et seulement s'il est possible de construire un rayon réfléchi sur la droite P'O. Ce qui signifie que cette droite P'O doit rencontrer le miroir. |
| Le champ d'un miroir, pour un point-objet donné, est la région de l'espace où se propage la lumière issue du point-objet et réfléchie par le miroir. |
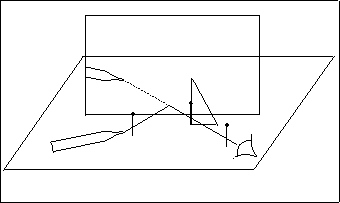
Déterminez le champ de votre miroir, par construction, pour votre dernier point-objet (celui qui n'était pas en face du miroir). Replacez sur la feuille le miroir, l'objet (dans la bonne position) et vérifiez votre construction.
Activité supplémentaire, ne figurant pas dans le document
d'accompagnement :
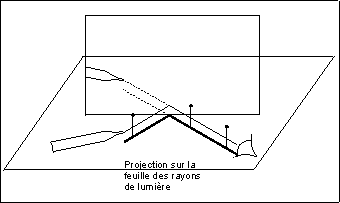
Déterminez le champ de votre miroir, dans l'espace. Votre construction
sur la feuille de papier est la projection sur la feuille (ramenée
donc à deux dimensions) du champ dans l'espace (à trois dimensions).
Cette remarque n'est peut-être pas à présenter aux
élèves (sauf s'ils se posent la question).
La loupe est choisie parce que familière aux élèves.
Ils savent ou peuvent facilement vérifier que si un objet est
situé assez près d'une loupe, celle-ci en donne une image
droite et agrandie. Cependant, ils ont tendance à penser que la
loupe rapproche l'objet, raison pour laquelle il paraît plus gros.
Il s'agit d'amener les élèves à comprendre que
la loupe donne une image plus éloignée de l'observateur que
l'objet, mais que c'est le diamètre apparent de l'image qui est
(en général) plus grand que celui de l'objet observé
à l'œil nu du même endroit. Cela devrait conduire les élèves
à bien différencier les notions de grandissement et de grossissement.
Ce sera aussi une introduction au rôle de l'oculaire dans un instrument
d'optique.
Protocole : Estimer la position à laquelle semble se trouver l'objet, estimer sa taille.
Conclusion : L'objet est plus près de la lentille et plus
petit que ce qui a été estimé.
Cette activité
pourrait être remplacée par l'activité
7 plus proposée au sous-paragraphe 13 2.
Vous pouvez acheter des loupes de marque Maped, formées d'une
lentille en verre d'environ 8 dioptries et de diamètre 50 ou 75
mm (50 mm conviennent parfaitement).
Une planche à dessin, une feuille de papier,
un support pour tenir la loupe verticale, posée sur la planche
à dessin, simple cale ou, plus pratique, petit pied de physique
avec une noix et une pince à trois doigts,
un objet, par exemple une carte de visite portant des inscriptions,
des traits verticaux espacés de 15 mm, ou des carrés adjacents
de 15 x 15 mm,
une cale pour tenir l'objet vertical sur la planche,
des épingles ou des réticules.
Une équerre peut servir de réticule, si on note à
chaque fois l'emplacement du sommet de l'angle droit.
Protocole : Repérez soigneusement sur la feuille de papier, la position de la loupe, la dimension de la loupe et la position du point-objet P choisi (à 7,5 cm de la loupe). Repérez, par des alignements d'épingles ou de réticules (vous pouvez vous aider avec une équerre), les rayons issus de P, émergeant de la lentille, pour deux positions de l'œil (écartées au maximum, pour la précision des tracés). Faites de même pour un deuxième point-objet Q. Construisez sur la feuille de papier les rayons provenant de P, puis ceux provenant de Q. Note : P et Q doivent être au niveau du milieu de la loupe.
L'image P'Q' est plus éloignée de la loupe que
l'objet PQ ;
L'image P'Q' est plus grande que l'objet PQ.
Activité
7 plus
Il est possible de trouver la position de l'image et sa taille approximatives
(avec une précision correcte) à l'aide d'un réticule
constitué par une équerre ou une règle graduées.
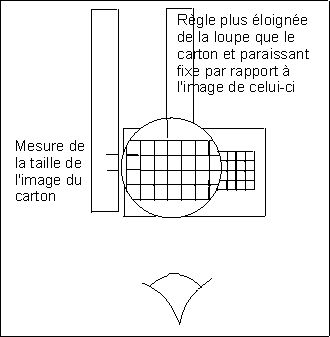
Choisissez comme objet un petit carton portant près de son bord
gauche un ou plusieurs rectangles de 15 x 15 mm, placé à
7,5 cm de la loupe. Observez-le à travers la loupe. Placez la règle
de manière à ce qu'en bougeant la tête, sa partie visible
directement au-dessus de la loupe paraisse fixe par rapport à l'image
du carton vu à travers la loupe. La règle doit être
plus éloignée de la loupe que le carton ; repérez
sa position. Déplacez légèrement la règle vers
la gauche, de manière que ses graduations soient visibles directement
et mesurez ainsi la taille de l'image d'un carré.
Résultats
A titre d'information, voici des résultats trouvés avec une loupe Maped de 5 cm de diamètre :
Distance objet - loupe : 7,5 cm ; distance horizontale entre les points
P et Q : 16,3 mm.
Distance image - loupe, pour P' 18 cm, pour Q' 17,8 cm. Distance P'
Q' : 35 mm.
L'utilisation d'un réticule (simple équerre) selon la méthode exposée au paragraphe suivant a donné une distance image - loupe d'environ 17 cm. Cette méthode n'est pas la plus précise, mais elle est très rapide et de plus utilisable même lorsque l'image est virtuelle ; il suffit que l'image (vue à travers la loupe) et le réticule (vu au-dessus de la loupe) ne se déplacent pas l'un par rapport à l'autre lorsque l'observateur déplace sa tête latéralement.
Soit (en anticipant sur la suite du cours, distance focale calculée de la loupe, 12,9 cm, grandissement mesuré 35 / 16,3 = 2,15, grandissement calculé selon les lois de conjugaison -17,9 / (-7,5) = 2,39. Distance focale de la loupe mesurée en formant sur un écran l'image d'un objet à l'infini, environ 12,5 cm.
Remarquons que ces résultats sont bons et qu'ils correspondent à une image virtuelle, d'étude difficile par les méthodes classiques.
Il faut impérativement que le plan d'incidence des rayons de lumière
soit parallèle au plan de la feuille de papier, pour que la figure
tracée sur la feuille soit identique au trajet réel des rayons
de lumière. Pour cela, les deux points-objets doivent être
au niveau du milieu de la loupe, les deux positions de l'œil, les plus
éloignées (pour une bonne précision des tracés)
étant là où P apparaît au bord de la lentille,
donc à l'extrémité d'un diamètre.
Des mesures effectuées en ne plaçant pas les points P et Q à mi hauteur de la lentille ont donné des images P' et Q' un peu trop proches de la loupe (17 cm au lieu de 17,8 cm, soit une focale f' de 13,4 cm au lieu de 12,9 cm). Ce n'est pas dramatique au niveau numérique, mais ennuyeux au niveau de la compréhension.
Protocole : Reprenez le protocole du travail pratique précédent.
Placez l'objet à 7,5 cm avant la loupe (lentille convergente). Que
voyez-vous en regardant à travers la lentille et en éloignant
l'objet de la lentille ? Essayez d'abord de prévoir le phénomène,
puis vérifiez expérimentalement. Lorsque l'objet est éloigné
de la lentille, il peut être utile de l'éclairer, par exemple
avec une lampe de bureau pour distinguer plus facilement son image.
Suite du protocole : Lorsque l'objet est éloigné
(1 mètre), effectuez une visée avec des épingles et
construisez deux rayons de lumière issus du point-objet P et traversant
la lentille. Où se trouve l'image P' ?
Placez dans le plan de l'image un réticule, ou simplement une équerre. Déplacez la tête latéralement et constatez que les positions relatives de l'image et du réticule ne changent pas. Approchez un peu le réticule de votre œil ; observez ce qui se produit lorsque vous déplacez la tête. Puis faites de même en éloignant le réticule.
Si au lieu du réticule,
vous employez une équerre graduée, vous pouvez mesurer la
taille de l'image. Pour vous persuader qu'il y a bien une image a l'endroit
trouvé (image comprise ici dans le sens d'une distribution lumineuse
qui peut impressionner une pellicule photographique placée directement
à cet endroit), vous pouvez y placer une feuille de papier blanc
ou une carte de visite. Il faudra éclairer vivement l'objet à
l'aide d'une lampe de bureau et peut-être faire la pénombre.
Placez l'objet (assez loin de la lentille) en différentes positions, en mesurant la distance p entre l'objet et la lentille. Dans chaque position, trouvez à l'aide d'un réticule (pour gagner du temps) la position de l'image et mesurez la distance p' entre la lentille et l'image. vérifiez que p et p' satisfont à la relation 1/p + 1/p' = C.
Calculez C exprimée en m-1 ou dioptries.
Observation : L'image est d'abord droite et plus grande que l'objet. Elle s'agrandit lorsqu'on commence à éloigner l'objet. Lorsque l'objet se trouve à plus de 13,2 cm de la lentille convergente, l'image apparaît floue. Il faut continuer à éloigner l'objet de la lentille et se reculer (éloigner son œil de la lentille) pour voir à nouveau l'image, cette fois renversée. Au fur et à mesure qu'on éloigne l'objet de la lentille, la taille de l'image diminue.
A partir du cas vu précédemment, où l'objet
est à 1 mètre environ de la lentille, les élèves
sont invités à chercher ce que devient la figure tracée
lorsque le point objet P est éloigné à l'infini, en
restant sur l'axe de symétrie de la lentille.
La réponse peut être trouvée par calcul et aussi, qualitativement en examinant la divergence, puis la convergence du faisceau de rayons de lumière issus du point-objet P et traversant la lentille convergente.
Sont alors énoncées les propriétés de deux rayons incidents particuliers, le rayon passant par le centre de la lentille qui n'est pas dévié et le rayon parallèle à l'axe (optique) qui émerge en passant par le foyer image F'.
Cela permet d'envisager les différents cas.
Les résultats trouvés précédemment peuvent être rapidement vérifiés à nouveau, qualitativement, en utilisant comme objet la flamme d'une bougie et en 'formant l'image' de la flamme sur un écran.
La bougie peut être remplacée par une lampe de bureau (voir
la liste de matériel conseillé
au début de cette page) ; si le professeur propose aux élèves
de réaliser ce TP chez eux, il n'aura pas à se reprocher
un éventuel incendie !
Vous pouvez consulter le document d'accompagnement ; vous pouvez
aussi consulter l'ouvrage : Terminales S, Physique Spécialité,
Ellipses, par l'auteur de ce
site Internet, J-M Jussiaux.
Le document d'accompagnement propose l'utilisation d'un tube en carton, portant les deux lentilles, objectif et oculaire.
Il est possible de réaliser une lunette sans ce tube, par exemple
en tenant les lentilles à la main (peu pratique), en les fixant
sur une règle en bois ou en les plaçant sur un banc d'optique
léger et en posant ce banc sur son épaule (sans blesser ses
camarades de classe).
Cela impose à l'élève une observation plus attentive
; à travers la loupe, une vaste zone de l'espace lui paraîtra
floue, et ce n'est que lorsque qu'il regardera, à travers la loupe
oculaire, en direction de l'objectif qu'il apercevra une image nette.
Des documents historiques montrent de telles lunettes, sans tube. Certains télescopes actuels sont eux aussi dépourvus de tube, remplacé par un treillis de barres métalliques.
Un tube en carton, ou une règle en bois, ou un banc d’optique,
une boite de lentilles diverses (+1 , 2 , 3 , 8 , ...), deux supports de
lentilles.
Ce paragraphe ne prétend pas remplacer une encyclopédie ;
il essaie plutôt de replacer les découvertes dans leur contexte
historique.
Vous pouvez aussi consulter l'ouvrage : Terminales S, Physique Spécialité,
Ellipses, par l'auteur de ce
site Internet, J-M Jussiaux.
Dès le Haut-Empire, les égyptiens travaillent le verre. La plus ancienne pièce de verre connue remonte à Aménophis I, entre 1557 et 1530 avant l’ère chrétienne. Lors de votre prochain passage au musée du Louvre, visitez les salles d'égyptologie ; vous y trouverez des flacons en verre de cette époque, étonnants par la richesse de leur couleurs et leur technique de fabrication : le verre n'est pas soufflé, mais moulé dans du sable, et le flacon est constitué de plusieurs pièces soudées les unes aux autres. Il reste encore à l'intérieur de certaines pièces le sable ayant servi à réaliser le moulage. Cette technique est encore employée de nos jours, pour couler les radiateurs en fonte, ou les blocs moteurs dans l'industrie automobile.
Thalès pose pour la première fois la question : « De quoi le monde est-il fait ? », en 585 avant notre ère, à Milet, cité grecque en Ionie. C'est la naissance de la Physique. Les mathématiques elles ont déjà plus de 1500 ans. Il serait intéressant de rapprocher cette interrogation scientifique, ce progrès de la connaissance, de l'organisation politique des cités grecques de l'époque, démocratique, du moins pour les citoyens grecs.
Mais la Grèce se retrouve assaillie de toutes parts. En 490 avant
notre ère, les athéniens arrêtent les perses à
Marathon. Tout cela conduit à une explosion de nationalisme religieux.
Une loi condamnant à mort quiconque donnera un enseignement sur
les choses du ciel est promulguée. Socrate, puis Platon, avec
tout leur prestige, approuveront cette séparation absolue du ciel,
domaine des dieux, et de la Terre, domaine des hommes. En 340 avant notre
ère, Aristote la justifiera dans son traité de physique qui
fera autorité durant 2000 ans, jusqu'à ce que Galilée
en démontre, au péril de sa vie, les contradictions.
Les religions se succéderont, mais ces interdits resteront,
retardant tout progrès scientifique.
En 323 avant notre ère, après la mort d’Alexandre,
ses généraux se partagent l’empire. Ptolémée
le premier fera de l’Egypte le centre scientifique du monde, avec la bibliothèque
d’Alexandrie qui comptera plus tard jusqu'à 500 000 livres.
En 47 avant notre ère, Jules César brûle la bibliothèque
d’Alexandrie.
Une verrerie est installée à Rome par Néron entre
54 et 68 de notre ère. Elle sera transférée à
Venise où elle est encore. Néron utilisait un monocle en...
émeraude ! Probablement importé d’Egypte. Est-ce pour cela
qu'il avait une curieuse façon de voir la vie en rose ?
La technique de fabrication du verre, matériau 'sensible' de l'époque doit rester secrète, ce qui explique que ce n’est qu’au VIIe siècle que des fours de verriers apparaissent en France. Lorsqu'un artisan verrier quitte Venise, sa famille est menacée de représailles ; si cela ne suffit pas, des tueurs sont envoyés à sa poursuite.
Pendant des siècles, c'est la science optique qui progresse le plus, sans doute parce qu'elle ne semble pas s'opposer aux interdits religieux. Et c'est elle qui conduira à l'éclatement des contradictions entre dogmatisme religieux et observations scientifiques.
En 990, le physicien arabe Al Haytam décrit les lentilles, connues
semble-t-il depuis plusieurs siècles. Dès cette époque,
donc, et sans doute même bien avant (consulter le point de vue personnel
de l'auteur, à la fin de cet article), sont connus tous les composants
nécessaires à la réalisation de la plupart des instruments
d’optique, y compris l’appareil photographique, puisque la première
photographie a été enregistrée sur du bitume de Judée.
Secret, interdits, manque d’intérêt économique,
expliquent sans doute que la science ait perdu près d'un millénaire.
En 1543, Copernic écrit que le Soleil est au centre du système solaire. Son ouvrage est toléré par l’Eglise car à caractère mathématique. Képler publie "L'astronomie nouvelle" en 1609, ouvrage résolument et ouvertement copernicien ; dès 1597, Galilée confie à Képler que lui aussi est depuis longtemps copernicien, mais que faute de preuve, il ne peut le déclarer publiquement. Notons que les rivalités entre église protestante et église catholique amèneront les uns à soutenir tout ce qui peut déplaire aux autres. Képler étant protestant, Galilée, catholique, cela explique que ce dernier ait connu les pires ennuis.
La première lunette d’approche est probablement construite par
l’italien Della Porta, en 1558. En 1608 est construite en Hollande la première
lunette efficace ; elle est considérée comme un divertissement,
et laisse les savants de l’époque totalement indifférents,
méfiants qu’ils sont de l’observation, de l’expérience et
du témoignage des sens. Ils suivent en cela les préceptes
dogmatiques d'Aristote, rejetant la pratique expérimentale, à
laquelle ils préfèrent les raisonnements scolastiques.
Ce n’est pas le cas de Galilée, qui enseigne à l’université
de Padoue, à 20 kilomètres de Venise, où, rappelons-le,
une verrerie existe depuis 1500 ans ! Il améliore la lunette, la
pointe vers le ciel et y trouve les justifications expérimentales
de la théorie de Copernic.
En 1610, il publie son « Messager des étoiles » : La Lune comme la Terre comporte des montagnes (C'est donc une pierre dans le royaume réservé aux dieux). Jupiter est accompagné dans sa rotation autour du Soleil par des satellites, comme la Terre est accompagnée par la Lune.
C'est pour l'Église catastrophique, car cela renverse par l'expérience, et non plus seulement par la pensée, tous les interdits : Le ciel, domaine réservé aux dieux, puis à Dieu, est parcouru par de vulgaires pierres. Consternation pour ceux qui avaient tranché : le ciel pour Dieu, la Terre pour les hommes, et sous la terre pour les enfers. Notons que ce sont ces interdits qui avaient conduit les hommes du moyen âge, à imaginer la Terre plate, alors que les philosophes grecs, non seulement ne doutaient pas de sa sphéricité, mais avaient même mesuré son diamètre ! Cette conception est, aujourd'hui encore, enfouie dans notre subconscient ; ne dit-on pas "la descente aux enfers". Pourquoi pas la "montée aux enfers" ? Le mouvement des satellites de Jupiter, accompagnant Jupiter dans sa trajectoire autour du Soleil, détruit un argument plus scientifique lui, élaboré par les jésuites : La Terre ne peut tourner autour du Soleil, car la Lune ne pourrait pas l'accompagner dans ce mouvement.
En 1618, l’Église déclare ces idées absurdes et hérétiques. Les ouvrages de Copernic sont interdits. Galilée est condamné en 1633 par l’inquisition ; il échappera de peu au bûcher, mais sera placé en résidence surveillée.
En 1610 encore, apparaît le microscope ; en 1671, le télescope. L’observatoire de Greenwich est le premier à en être équipé.
Les navigateurs sont à la recherche d’horloges de plus en plus
précises. Les satellites de Jupiter semblent en constituer une.
Mais des irrégularités sont mesurées. En 1675, le
danois Römer les attribue à la vitesse de propagation de la
lumière qu’il mesure ainsi pour la première fois.
En 1861, l’Écossais James Clerk Maxwell, vient d’être
licencié de son poste d’enseignant, à Aberdeen, car à
la suite de la fusion de deux universités, il y avait un physicien
de trop. Nous saluerons, au passage la perspicacité de ses confrères
! Cela lui laisse enfin le temps de se consacrer à ses recherches
personnelles ; nous dirions aujourd'hui qu'il a su rebondir. Il regroupe,
en quelques équations, toutes les connaissances des physiciens en
électricité et magnétisme, puis il trouve à
ce système d’équations une solution encore inconnue, une
onde électromagnétique se propageant à une vitesse
c, telle que, en utilisant les notations actuelles, E0 u0
c2 = 1. La mesure très délicate des deux premières
constantes a été faite en 1856 par les allemands Kohlrausch
et Weber , ce qui conduit à c = 3,107 . 108 m . s-1.
Or, en 1850, le français Fizeau a trouvé pour vitesse de
la lumière, c = 3,14 . 108 m . s-1
. Maxwell écrit : « on ne peut guère éviter
d’en déduire que la lumière est une onde électromagnétique
», formulation d'une extraordinaire modestie, pour une découverte
capitale. L’équation précédente impose que c soit
une constante physique. Que l’on s’éloigne ou se rapproche de la
source, on reçoit l’onde à la même vitesse c. Cela
est vivement reproché à Maxwell. A tort, car ses équations
sont en accord avec la relativité. En 1881, l’américain Michelson
vérifiera que la vitesse de la lumière est bien une constante
physique.
En 1939, est inventé le microscope électronique. Le premier laser entre en fonctionnement en 1960. Les progrès récents de l’optique doivent beaucoup à l’informatique. Vers 1902, il fallu plusieurs années, au docteur Rudolph, de la firme Zeiss pour calculer un objectif comportant quatre lentilles, qui fut nommé Tessar, utilisé encore aujourd'hui dans des variantes modernisées. Les objectifs à focale variable actuels peuvent compter plus de vingt lentilles, et dans des positions qui sont modifiables ; ils sont calculés et optimisés par des moyens informatiques.
La microscopie en champ proche, les grands télescopes à optique active, nécessitent un traitement informatique de l'image associé à un pilotage informatique de la partie 'optique'.
Lors de la visite du Musée de la civilisation anatolienne,
à Ankara, capitale de la Turquie (pays dont je conseille la visite,
en dehors de toute considération politique), notre guide nous a
présenté des miroirs, miroir d'eau et miroir en obsidienne.
Le miroir d'eau ressemble à une casserole de faible profondeur, et de couleur foncée. C'est un instrument d'optique puisqu'il donne une image, mais il est directement inspiré de la nature.
Le miroir d'obsidienne, datant du Néolithique, soit environ 5000
ans avant notre ère, est taillé dans une pierre très
dure et au grain très fin, de couleur noire. Or des trois miroirs
exposés dans une vitrine, un était grossissant !
Pour grossir, un miroir doit être concave, ce qui est difficile
à réaliser. Il est donc difficile d'imaginer qu'il a été
construit par hasard. Il est possible de concevoir le schéma suivant
:
Pour réaliser une surface bien plane, de qualité optique, il suffit d'user l'une par l'autre deux surfaces à peu près planes. C'est la technique encore en usage.
Pour obtenir une surface sphérique, il faut frotter la surface à user sur une calotte sphérique, en combinant plusieurs mouvements, technique encore en usage.
Il est possible d'imaginer qu'en essayant de réaliser une surface plane, si les bords sont trop usés, on obtienne une surface sphérique convexe. Cette surface convexe peut servir à réaliser une surface concave.
Le premier instrument d'optique remonte donc, à mon avis à
7000 ans ! En associant deux de ces miroirs, il aurait été
possible, dès cette époque de réaliser un téléscope.
Pour vérifier cette hypothèse, il faudrait étudier
l'état de surface des miroirs d'obsidienne, vérifier s'ils
sont ou non proches de la qualité optique, puis vérifier
si le rayon de courbure du miroir concave est constant, afin de retrouver
sa technique de fabrication. Ces vérifications ne sont pas destructives.
Il serait intéressant aussi de rechercher si d'autres miroirs
grossissants ont été trouvés, et de retrouver des
outils ayant servi à leur fabrication.
Veuillez noter que les lois de conjugaison que vous devez
étudier dans cette classe de première S, ne s'appliquent
pas à l' œil, car les milieux qui baignent la 'lentille' ne
sont pas les mêmes de part et d'autre. Il n'y a pas symétrie,
or les lois de conjugaisons sont symétriques.
Ces lois peuvent s'appliquer, à condition de remplacer les distances
p et p' par les chemins optiques, produits des distances parcourues par
l'indice optique du milieu.
Source : Électronique n° 68, Mars 1997.
Voici quelques informations extraites d'un article rédigé
par des ingénieurs cherchant à reproduire par l'électronique
et l'informatique, les mécanismes de la vision humaine.
L' œil comporte 4 à 5 millions de cônes sensibles à la couleur, dont seulement 15 % pour le bleu (les autres pour le rouge et le vert), dans la zone de l'axe optique. Il comporte aussi 140 millions de bâtonnets panchromatiques (sensibles à toutes les couleurs), 35 fois plus sensibles que les cônes, et dont la densité est décroissante jusqu'à la périphérie.
On observe un mouvement de saccade oculaire : L' œil balaye à 2 ou 3 Hz un angle de 20 °, ce qui permet la détection dynamique des contours. A cela s'ajoutent des mouvements vibratoires à 100 Hz, de faible amplitude angulaire, correspondant à l'acuité visuelle, différentiation entre deux pixels adjacents, cônes ou bâtonnets : L'image d'un point lumineux formée par le cristallin sur la rétine excite alternativement deux cellules sensibles voisines.
Le nerf optique comporte 1 million de fibres. Il véhicule une information déjà compressée, dans un rapport 1 / 145. Ceci est certainement à l'origine de certaines illusions d'optique.
La lumière n'est pas visible, sauf si elle pénètre
dans l'oeil.
Un objet est vu si la lumière qu'il émet ou qu'il renvoie
pénètre dans l'oeil de l'observateur.
La lumière est une onde électromagnétique qui
échange son énergie par "grains d'énergie" appelés
photons. Elle se propage en ligne droite dans le vide et dans les milieux
transparents homogènes. Elle est attirée par les masses.
Le rayon lumineux est un modèle simple qui permet de résoudre
une partie des problèmes d'optique.
Pour illustrer la notion de modèle, Vous pouvez aussi consulter
notre recherche effectuée dans le cadre des Olympiades de la Physique
2004-2005, correction de l'aberration chromatique d'une lentille réfractive
convergente, par une lentille diffractive
convergente.
Une lentille (en verre, plongée dans le vide ou dans l'air)
à bord mince est convergente, une lentille à bord épais
est divergente.
Un miroir est formé par une surface lisse réfléchissante
(métal) ou partiellement réfléchissante (exemples,
verre, eau , obsidienne).
Le rayon réfléchi est dans le plan d'incidence défini
par le rayon incident et la normale à la surface réfléchissante.
L'angle de réflexion est égal à l'angle d'incidence.
Un miroir plan donne d'un objet une image symétrique par
rapport au plan du miroir.
// Si l'objet est réel (un vrai objet matériel par
exemple), l'image est virtuelle : elle est visible directement par l'oeil
de l'observateur, mais nécessite un objectif pour être formée
sur une plaque photographique, ou un capteur CCD.
Un miroir plan donne d'un point-objet M une image ponctuelle M' (point-image), symétrique de M par rapport au miroir.
La loupe, l'objectif d'un appareil photographique, le monocle d'un
hypermétrope, sont des lentilles convergentes.
L'axe optique est orienté dans le sens de propagation de la
lumière, de gauche à droite.
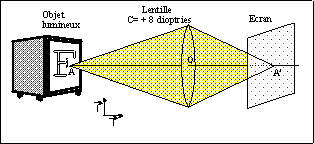
Un objet situé à l'infini, avant la lentille, a une image
renversée située après la lentille, à une distance
f de celle-ci, appelée distance focale.
Un objet situé avant la lentille, à une distance égale
à f, a une image située à l'infini, après la
lentille.
Un objet situé avant la lentille entre ces deux positions a
une image renversée située après la lentille, à
une distance finie, supérieure à f.
Si l'objet est avant la lentille, à une distance plus courte
que f, son image est droite, située avant la lentille.
La vergence C d'une lentille, mesurée en dioptrie (symbole
d)
ou m-1, est l'inverse de la distance focale f mesurée
en mètre.
// Expériences
de cours sur tableau magnétique
1. Tout rayon incident parallèle à l'axe optique émerge en passant par le foyer image F'.2. Tout rayon passant par le centre optique n'est pas dévié.3. Tout rayon incident passant par le foyer objet F émerge parallèlement à l'axe optique |
Nous devons définir un repère (O, i, j). En posant
p = OA, p ' = OA' et f ' = OF',
la relation entre les positions de l'objet et de son image s'écrit
:
- 1 / p + 1 / p ' = 1 / f ' |
g = |
